1 Beispiel 5 (Einige stetige Dichten, Formulierung als Aufgabe
Werbung
1
Beispiel 5 (Einige stetige Dichten, Formulierung als Aufgabe)
Illustration 1
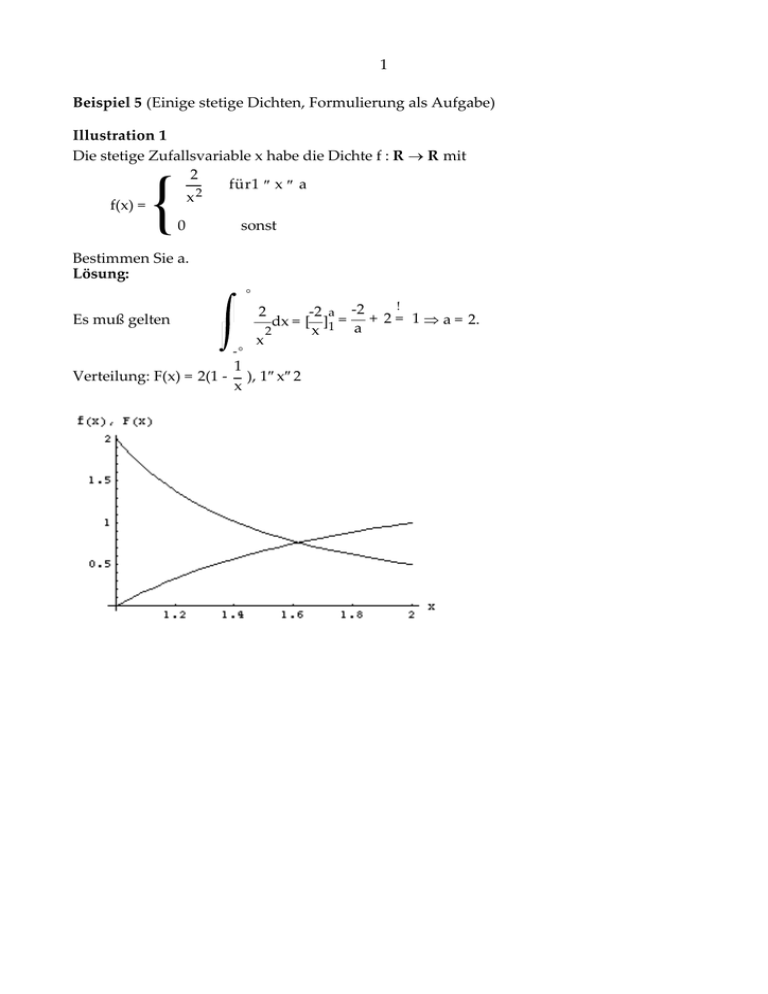
Die stetige Zufallsvariable x habe die Dichte f : R → R mit
2
für1 ≤ x ≤ a
x2
f(x) =
0
sonst
{
Bestimmen Sie a.
Lösung:
∞
-∞
Verteilung: F(x) = 2(1 -
!
-2 a -2 + 2 =
1 ⇒ a = 2.
=
dx = [ ]1 a
2
x
2
Es muß gelten
x
1
), 1≤x≤2
x
2
Illustration 2 (eine Aufgabe zu einer Dichte aus der Zuverlässigkeitstheorie)
Die Dichtefunktion der Zufallsvariablen X, welche die Lebensdauer eines elektronischen
Bausteins in Stunden angibt, ist gegeben durch
f(x) =
{
10
x
2
0,
, x > 10
x ≤ 10
a)Bestimmen Sie die Verteilungsfunktion von x.
b) Mit welcher Wahrscheinlichkeit funktioniert ein solcher Baustein länger als 20
Stunden?
c) Was ist die Wahrscheinlichkeit, daß von 6 solchen Teilen mindestens 3 jeweils mindestens 15 Stunden funktionieren?
Lösung:
x
a)
F(x) =
10
10
y2
10 x
10
=+ 1 , 10≤x
y 10
x
dy = -
20
∞
10
b)
20
x
2
10
dx = 1 10
x
2
dx = 1 +
10 20
1
1
10 = 1 + - 1 =
x
2
2
3
c) Die Wahrscheinlichkeit, daß ein Bauteil mindestens 15 Stunden funktioniert, ist
15
p = P(X ≥ 15) = 1 - P(X< 15)= 1 -
10
2
10
x
dx = 1 -F(15) = 1 -
1 2
=
3 3
2
also p = .
3
Sei nun Y die Zufallsvariable, die die Anzahl der mindestens 15 Stunden funktionie2
renden Bauteile angibt. dann ist Y binomialverteilt Y ~ B(n, p) mit n = 6 und p = :
3
2
Y ~ B(6, ). Die gesuchte Wahrscheinlichkeit ist P(Y ≥ 3). Damit folgt aus direkter
3
Auswertung der Binomialverteilung
6 2 0 1 6 6 2 1 1 5 6 2 2 1 4
P(Y ≥ 3) = 1 - P(Y ≤ 2) = 1 0 3 6
1 3 6
2 3 6
1
12 60 656
=1=
= 0.9
729 729 729 729
Illustration 3 (zur Normierung)
Die Dichte einer Zufallsvariablen X sei
f(x) =
{
2
c (4x-2x )
0
für 0<x<2
sonst
Bestimmen Sie
a) die Normierungskonstante c,
b) die Verteilung sowie
c) P[ 1/2 < X < 3/2 ]
Lösung
Beachten Sie: Die Normierungkonstate ist 3/8, damit folgen für die Dichte und die
Verteilung:
f(x) = 3(2 - x)x/4
F(x) = (3 - x)x2/4, denn
2
16
8
3
u3 2
f(u)du = c(2u2 - 2
) = c(8 )= c = F(2) = 1 ⇔ c =
3 0
3
3
8
0
1
3
2x 3
3
1
F(x) = (2x 2 –
) = x 2 – x 3 = x2(3-x), F(0) = 0, F(2) =1
8
3
4
4
4
P[ 1/2 < X < 3/2 ] = F(3/2) - F(1/2) = 11/16
4
Die Dichte
f(x) = 3x(2-x)/8
Die Verteilung
F(x) = x2(3-x)/4
5
Illustration 4 (zur Normierung)
Gegeben sei die folgende Dichte f:
c.x -2≤ x ≤0
f(x) = { x - 2 2≤ x ≤3
0
sonst
Bestimmen Sie c und die Verteilungsfunktion F.
Lösung
3
c 2
0
3
x2
9
1
cxdx
=
x
=
2c
(1)
(2)
(x
2)dx
=
2x
=
62
+
4
=
-2
2
-2
2
2
2
2 2
1
1
(1)-(2) ⇔ -2c + = 1 ⇔ c = 2
4
Damit folgt für die Verteilung aus
0
|
1
z2 0 1 1 2
(- z)dz =- | = - x , -2≤ x ≤0 und
8 –2 2 8
–2 4
x
2
z2
x x
(z -2)dz =(
-2z)| =
-2x + 2 , 2≤ x ≤3 und damit
2
2
2
2
x
F (x) = {
0
x≤-2
0.5 -0.125x 2
-2<x<0
0.5
0≤x<2
0.5x 2 - 2x + 2.5
2≤x<3
1
x≥3
6
Die Dichte:
Die Verteilung:
insgesamt











