Aufgabe 23 Eine Zufallsvariable X sei

Statistik II für Studierende der Soziologie und Nebenfachstudierende
Prof. Dr. Thomas Augustin, Gero Walter
Übungsblatt 7
SoSe 2010
Aufgabe 23
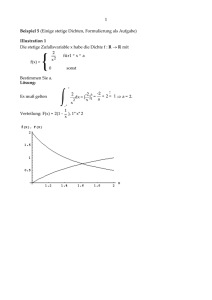
Eine Zufallsvariable X sei standardnormalverteilt.
a) Skizziere die Dichte sowie die Verteilungsfunktion.
b) Bestimme die Wahrscheinlichkeit für die Menge {X < 1.96} aus der Tabelle.
c) Wie findet man graphisch anhand der Dichte bzw. anhand der Verteilungsfunktion die gesuchte Wahrscheinlichkeit?
Aufgabe 24
Formuliere das schwache Gesetz der großen Zahlen und interpretiere es anschaulich.
Aufgabe 25
Das Gewicht von Zuckerpaketen sei normalverteilt mit µ = 1000 Gramm und
σ = 12 Gramm.
a) Wie groß ist die Wahrscheinlichkeit, dass das Gewicht von einem Zuckerpaket mindestens 996 Gramm und höchstens 1004 Gramm beträgt?
b) Angenommen, man hat 9 Zuckerpakete und ist interessiert am durchschnittlichen Gewicht. Wie groß ist die Wahrscheinlichkeit, dass das durchschnittliche Gewicht mindestens 996 Gramm und höchstens 1004 Gramm beträgt?
Aufgabe 26
Die Zufallsvariablen Xi , i = 1, . . . , n seien unabhängigPidentisch normalverteilt
2
mit µXi = 0 und σX
= 1. Die Zufallsvariable X̄n = n1 ni=1 Xi ist dann normali
2
verteilt mit µX̄n = 0 und σX̄
= n1 .
n
a) Skizziere die Dichte von X̄n für verschiedene Werte von n.
b) Betrachte Intervalle der Art [µX̄n − c , µX̄n + c]. Wie ändert sich die Wahrscheinlichkeit für X̄n ∈ [µX̄n − c , µX̄n + c] in Abhängigkeit von n?