Lösungen ¨Ubungsklausur

Lösungen Übungsklausur
Aufgabe 1
Definiere die Ereignisse
I = {Person ist infiziert}
T = {Test ist positiv}
In der Aufgabenstellung sind folgende Wahrscheinlichkeiten gegeben
P(T | I c ) = 0,01
P(T | I) = 0,9
P(I) = 0,001
a) Gesucht ist P(T ).
P(T ) = P(T | I)P(I) + P(T | I c )P(I c )
= 0,9 · 0,001 + 0,01 · 0,999
= 0,01089
Die Wahrscheinlichkeit, daß der Test einen positiven Befund liefert beträgt
ungefähr 0,01.
b) Gesucht ist P(I | T ).
P(I | T ) = P(T | I)
P(I)
0,001
= 0,9 ·
= 0,0826
P(T )
0,00091
Die Wahrscheinlichkeit, daß eine Person mit positivem Befund tatsächlich infiziert ist, beträgt ungefähr 0,08.
c) Bezeichne X die Anzahl der positiven Testbefunde. Dann gilt X ∼ B(500, P(T ))
und daher
EX = 500 · 0,01089 = 5,445
varX = 500 · 0,01089 · 0,98911 = 5,386
d) Poisson-Approximation:
Sei X ∼ B(n, p) und Y ∼ P(λ) mit λ = np dann gilt Y ≈ X.
Hier gilt demnach Y ∼ P(λ) mit λ = 500 · 0,01089 = 5,445.
Damit ist zu berechnen:
P(3 ≤ Y ≤ 6) = P(Y = 3) + . . . + P(Y = 6)
λ3 −λ λ4 −λ λ5 −λ λ6 −λ
e +
e +
e +
e
=
3!
4!
5!
6!
µ
¶
1
λ
λ2
λ3
−λ 3
=e λ
+
+
+
6 24 120 720
= 0,603
Die Wahrscheinlichkeit, zwischen drei und sechs positiven Befunden zu beobachten beträgt ungefähr 0,60.
1
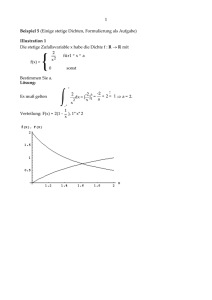
Aufgabe 2
RR
!
a) Für eine Dichte muß gelten:
fX,Y (x, y) dx dy = 1
Z 1Z 1
Z 1h
i1
2 2
3 2
1 2
k
x + 3x y dx dy = k
x + x y dy
2
0
−1 0
−1
Z 1
1
=k
+ y 2 dy
2
h
=k
−1
1
y
2
¡1
+ 31 y 3
1
3
=k 2+ −
= k 53
Daraus folgt, für k =
3
5
i1
−1
(− 12
¢
− 13 )
ergibt das Integral über fX,Y (x, y) gerade eins.
b) Berechne zunächst die marginalen Dichten.
In Teil a) wurde bereits berechnet:
(
3 1
( + y 2 ) −1 ≤ y ≤ 1
fY (y) = 5 2
0
sonst
Bestimme nun die marginale Dichte von X:
Z 1
fX (x) =
fX,Y (x, y) dy
−1
Z 1
3
=5
x + 3x2 y 2 dy
=
3
5
h
−1
2 3
xy + x y
i1
−1
= 65 (x + x2 )
Also insgesamt:
(
fX (x) =
6
5
(x + x2 ) 0 ≤ x ≤ 1
0
sonst
Man sieht direkt, daß fX (x) · fY (y) 6= fX,Y (x, y). Daher sind X und Y nicht
unabhängig.
R
c) Berechne die marginale Dichte über fU (u) = fX,U (x, u)
und die gemeinsame Dichte fX,U (x, u) = fX,Y (x, u − x) nach dem Transformationssatz.
Bestimmung der Integrationsgrenzen:
fX,Y (x, u − x) > 0, falls
0≤x≤1
−1 ≤ u − x ≤ 1
⇔
2
u−1≤x≤u+1
und damit insgesamt max(0, u − 1) ≤ x ≤ min(1, u + 1).
Es sind drei Fälle zu unterscheiden:
1. Fall
2. Fall
3. Fall
−1 ≤ u ≤ 0
0≤u≤1
1≤u≤2
=⇒
=⇒
=⇒
0≤x≤u+1
0≤x≤1
u−1≤x≤1
Hierzu benötigt man
Z b
Z b
2
2
3
3
(x + 3x (u − x) ) dx = 5
x + 3x2 (u2 − 2ux + x2 ) dx
5
a
a
Z b
= 53
x + 3u2 x2 − 6ux3 + 3x4 dx
a
h
ib
= 53 12 x2 + u2 x3 − 32 ux4 + 35 x5
a
Und es ergibt sich für die Dichte
1. Fall −1 ≤ u ≤ 0
Z
u−1
fU (u) =
fX,U (x, u) dx
0
=
3
5
h
1 2
x
2
+ u2 x3 − 32 ux4 + 35 x5
iu+1
0
= 35 ( 12 (u + 1)2 + u2 (u + 1)3 − 32 u(u + 1)4 + 53 (u + 1)5 )
2. Fall 0 ≤ u ≤ 1
Z
1
fU (u) =
fX,U (x, u) dx
0
= 35 ( 21 + u2 − 32 u + 35 )
9
= 33
− 10
u + 35 u2
50
3. Fall 1 ≤ u ≤ 2
Z
fU (u) =
=
1
fX,U (x, u) dx
u−1
3 11
( − 32 u + u2 ) − 53 ( 12 (u
5 10
− 1)2 + u2 (u − 1)3 − 32 u(u − 1)4 + 35 (u − 1)5 )
4. Fall u < −1 oder u > 2
fU (u) = 0
3
Aufgabe 3
uiv
Seien X1 , . . . , Xn ∼ Exp(λ)
und Gn = min1≤i≤n Xi
a) Die Verteilungsfunktion exponential-verteilter Zufallsvariablen ist bekannt:
FXi (x) = FX1 (x) = 1 − e−λx
Damit kann man die Verteilungsfunktion berechnen
P(G2 > c) = P(X1 > c, X2 > c)
= P(X1 > c)P(X2 > c)
= (1 − P(X1 < c))(1 − P(X2 < c))
= (1 − FX1 (c))2
= e−2λc
b) Analog zu a) folgt
P(Gn > c) = (1 − FX1 (c))n = e−nλc → 0
für n → ∞
c) Es ist zu zeigen P(|Gn | > ε) → 0 für beliebiges ε > 0 und n → ∞. Da Xi
immer positiv ist (für alle i), gilt auch Gn > 0 und daher |Gn | = Gn .
P(|Gn | > ε) = P(Gn > ε) = e−nλε → 0 für beliebiges ε > 0
Alternativ kann man die Wahrscheinlichkeit mittels der Chebychev/MarkovUngleichung durch das erste oder zweite Moment abschätzen. Es gilt Gn ∼
Exp(nλ) und die Momente sind aus der Vorlesung/Übung bekannt.
4