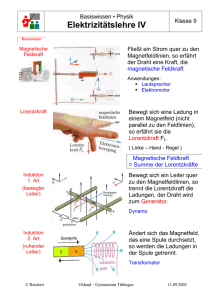
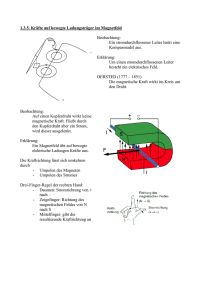
Ph Q11 Mathematische Beschreibung des Magnetfeldes

Ph Q11 Mathematische Beschreibung des Magnetfeldes
… formal analog zum elektrischen Feld
Man beschreibt sogar die fiktiven Pole eines Dauermagneten oder Elektromagneten wie
Magnetladungen im Abstand d über Gleichungen analog dem Faradaygesetz.
Man konstruiert eine exp. realisierbare Messsituation:
Stromführendes Leiterstück ( Strom J ; Länge s ) wird senkrecht zum homogenen Feld B
bewegt.
Da Dauermagneten nicht ausreichend spezifizierbar und berechnebar sind, verwendet man das
Feld im Innern langgestreckter Kreisspulen ( Quersdchnitt A ; Windungszahl N auf Länge L ;
Spulenstrom i )
EXP: Gemessen wird die Feldkraft F in Abhängigkeit von allen Parametern N/L ; J ; i ; A
Man findet angenähert stets einfache Proportionalität und Unabhängigkeit von A !
Es ist also F ~ N/L · i · J · s
Das Produkt N/L · i beschreibt den Felderzeuger
Das Produkt J · s den Probanden
In Anlehnung an F = qE schreibt man i · N/L als magnetische Feldstärke H
Damit gilt formal: F ~ Js · H
Da N dimensionslos ist, hat H die Dimension [ H ] = A/m mit der Einheit 1 A/m
Vgl. [ E ] = V/m
Dahinter verbirgt sich aber keine tiefe Weisheit !
Info: das Erdmagnetfeld hat an den Polen eine typische Stärke von 15 A/m
Eigenstudium:
eine clevere Definintion der Stromstärke erlaubt eine Berechnung der Propkonstante in
F ~ Js · H im Vakuum
F = (4π·10-7 Vs/Am) · Js · H
Man bezeichnet die Konstante (4π·10-7 Vs/Am) als magnetische Permeabilität μo des
Vakuums ( vergleichbar der Dielektriztitätkonstante εo )
Und in Anlehnung an D = εo E definiert man eine Größe B = μo H
Da H nur bei Normspulen einen Sinn macht, benutzt man i.a. die Größe B
Es ist also F = Js · B
Überlege: [ B ] = N / Am = Vs/m²
Man nennt 1 Vs/m² = 1 Tesla , kurz 1T
Historisch: 1 Gauß = 10-4 T
Das Erdmagnetfeld hat an den Polen eine Stärke von 20 μT
Schulmagneten haben typische Stärken von 0,001 T bis zu max 0,1 T an den Polen.
Die derzeit stärksten Industriemagnete haben lokal bis zu 10 T.
Die Einheit 1 Vs/m² weckte historisch den Eindruck, dass das Feld B durch den Querschnitt
A „fließt“ …
Daher der Name magnetische Flussdichte für B
Ergänzend:
Analog zu D = εr ·εo · E schreibt man B = μr · μo · H
mit der relativen magnetischen Permeabilität μr
μr hat Werte im Bereich 10-6 bis 106 je nach Medium und Stoff
Es gibt abweichend vom elektrischen Feld ein merkwürdiges, nicht trivial verständliches
Phänomen:
μr > 1 ] Paramagnetismus
Paramagnetische Stoffe verstärken ein Magnetfeld in ihrem Innern, sie erzeugen also ein
sekundäres Feld gleicher Orientierung
μr < 1 ] Diamagnetismus
Diamagnetische Stoffe schwächen ein Magnetfeld in ihrem Innern, sie erzeugen ein
Gegenfeld.