Energie und mechanische Arbeit

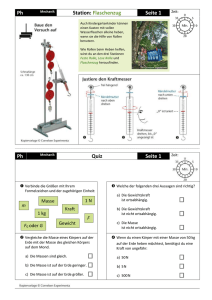
2007/2008
Physik– Energie
Lehrtext
Energie zeigt sich in Arbeit
Versuchsbeschreibung
Wir machen den folgenden Versuch mit der Holzbahn:
Wir lassen einen Wagen mit der Masse m = 42 g von einer Schanze beschleunigen und in die
Ebene fahren. Am Ende der Schanze wird mit einem Lichtschrankenpaar die Geschwindigkeit
des Wagens ermittelt. Mit Hilfe Stoppuhr wird außerdem die Zeit ermittelt, die der Wagen bis
zum Stillstand benötigt.
Protokollierung der Messwerte:
Messgröße
Messwert
Zeitdifferenz zwischen Lichtschranken ∆t1 in s
0,065 s
Bremszeit ∆t2 in s
1,78 s
Distanz zwischen den Lichtschranken∆s1 in m
0,0250
Bremsweg ∆s in m
0,51 m
Auswertung der Messdaten
• Nach dem Verlassen der Schanze wird der Wagen abgebremst. Er verringert seine Geschwindigkeit und erfährt daher eine Bremsbeschleunigung. Weil der Wagen seine Geschwinidigkeit ändert wirkt auf ihn eine Kraft, nämlich die Reibungskraft der Schiene.
Nach Newton 2 gilt:
F = ma
Um diese Kraft zu bestimmen, muss man nun zunächst aus den Messdaten die Beschleunigung bestimmen:
0,025 m
m
v=
= 0,385
0,065 s
s
a=
c 2007–10–14 by Markus Baur using LATEX
∆v
∆tb
Seite: 1
2007/2008
Physik– Energie
Lehrtext
m
1,78 s
s
m
a = 0,216 2
s
Damit lässt sich nun die Bremskraft F des Wagens bestimmen:
a = 0,385
F = ma
F = 0,042 · 0,2 N = 8,4 · 10−3 N
• Aus den Messdaten ist zusätzlich die kinetische Energie zu bestimmen:
1
Ekin = mv 2
2
kgm2
1
· 0,042 · 0,42 2
2
s
−3
Ekin = 3,36 · 10 J
Ekin =
• Deutung der Energie- Erhaltung: Es ist bekannt, dass die Energie eine Erhaltungsgröße
ist. Aus diesem Grund muss kann die kinetische Energie nicht verschwunden sein, auch
wenn der Wagen am Ende der Bremsstrecke stehen bleibt.
Die kinetische Energie wurde dazu verwendet, dass der Wagen in
der Ebene die Strecke ∆s zurücklegt, auf der gleichzeitig die Bremskraft F auf ihn wirkt.
• Berechnung des Produkts aus Bremskraft und Bremsweg. Dieses Ergebnis wird im Anschluss mit dem Wert der kinetischen Energie verglichen:
F · ∆s = 8,4 · 10−3 · 0,45 Nm
F · ∆s = 3,78 · 10−3 Nm
Vergleicht man nun diesen Wert mit der kinetischen Energie und ersetzt in der Einheit
1 kg·m
= 1 N, dann gilt:
s2
Ekin = 3,36 · 10−3 Nm
Vergleicht man die beiden Werte, dann stellt man im Rahmen der Messgenauigkeit fest:
Ekin = F · ∆s
Dieses Produkt aus Kraft und Weg hat einen bestimmten Namen:
Wirkt eine konstante Kraft F parallel zu einer Weglänge ∆s, dann
ist das Produkt aus den beiden Größen die von einem Körper geleistete Arbeit W . Man kann dies in der Formelsprache ausdrücken:
W = F · ∆s
c 2007–10–14 by Markus Baur using LATEX
Seite: 2
2007/2008
Physik– Energie
Lehrtext
Weitere Betrachtungen
• Die Einheit der Energie und der Arbeit ist [E] = [W ] = 1 Nm.
• Die kinetische Energie in unserem Versuch wurde dazu benötigt, damit der Wagen die
Arbeit W verrichten konnte.
Aus dieser Betrachtungsweise ist nun auch der Zusammenhang zwischen den Größen Energie
E und Arbeit W ersichtlich:
Die Energie eines Körpers ist die Fähigkeit eines Körpers Arbeit
verrichten zu können. Verrichtet ein Körper eine mechanische Arbeit, dann ist dazu Energie nötig und es gilt
∆E = W
Die Arbeit und die Goldene Regel der Mechanik
Einführung
Beim Bau der Mittelstation der Wankbahn wurden im Frühjahr 1982 die maschinellen Bauteile
mit der alten Wankbahn mit Hilfe eines motorbetriebenen Flaschenzug zur Baustelle transportiert.
Für einen derartigen Transport sind die folgenden Fragen von Interesse:
1. Der Motor der Seilwinde liefert Energie. Erkläre, für was die Motorenergie bei dem Transportvorgang benötigt wird.
2. Die Maschienenbauteile hatten eine maximale Masse von 1,8 t. Bestimme die maximale
Zugkraft des Motors, die er beim Anheben der Bauteile mindestens besitzen muss.
3. Aus dem Bild ist ersichtlich, dass die Hubhöhe der Bauteile 9,0 m betrug. Wie viel Meter
Seil muss der Flaschenzug daher mindestens besitzen?
Um eine Antwort auf diese Fragen zu geben macht man nun den folgenden Modellversuch:
c 2007–10–14 by Markus Baur using LATEX
Seite: 3
2007/2008
Physik– Energie
Lehrtext
Man hängt nun mehrere Körper von verschiedener Masse an den Flaschenzug und liest jeweils
die Werte für die Kräfte F1 und F 2 sowie die Gewichtskraft G ab.
Als Ergebnis dieses Versuchs kommt man zu folgendem Schluss:
Die lose Rolle halbiert die Gewichtskraft des Körpers. In jedem der
beiden tragenden Seile greift die halbe Gewichtskraft des Körpers
an:
G
FZug =
2
Dieses Gesetz der Kraftvermittlung kann man mit Hilfe der tragenden Seile noch verallgemeinern:
FZug =
G
Anzahl der tragenden Seile
Mit Hilfe dieses Kraftvermittlungsgesetzes kann man nun die maximale Zugkraft des Motors
der Seilwinde bestimmen:
Da die Anzahl der tragenden Seile 2 ist, muss die benötigte Zugkraft
FZug =
17658
N = 8829 N = 8,8 kN
2
betragen.
Um die zweite Frage zu beantworten, Stellen wir den Körper auf den Versuchstisch und ziehen
den Flaschenzug stramm. Mit einem Filzsitft markiert man die Seilposition an der oberen Umlenkrolle. Nun zieht man den Körper um 10cm nach oben.
Man erkennt:
c 2007–10–14 by Markus Baur using LATEX
Seite: 4
2007/2008
Physik– Energie
Lehrtext
Die durch den Flaschenzug laufende Seillänge ist das Doppelte von
der Hubhöhe. Ist n die Anzahl der tragenden Seile, dann kann man
die benötigte Seillänge s bestimmen durch die Gleichung
s=n·h
Man kann nun die zweite Frage mit diesem Gesetz beantworten: Da n = 2 ist benötigt man bei
einer Hubhöhe h = 9,0 m insgesamt:
s = 2 · 9,0 m = 18 m
Seil.
Die vom Motor zur Verfügung gestellte Energie wird nun dazu verwendet, dass das Maschinenbauteil die Hubarbeit W verrichten kann. Die Hubarbeit kann man nun berechnen über:
W =F ·s
W = 8829 N · 18 m
W = 158922 Nm
Vergleicht man dies nun mit der Arbeit, die man ohne Flaschenzug hätte verrichten müssen:
W = 17658 N · 9,0 m
W = 158922 Nm
Vergleicht man die beiden Werte, dann erhält man das folgende Resultat:
Bei einem Kraftwandler wie dem Flaschenzug wird die Kraft verkleinert, die geleistete Arbeit bleibt aber konstant. Das bedeutet,
dass im gleichen Maß wie die Kraft reduziert wird, der benötigte
Weg sich verlängert. (Goldene Regel der Mechanik) In Formelsprache:
1
FZug = · G ⇒ s = n · h
n
c 2007–10–14 by Markus Baur using LATEX
Seite: 5