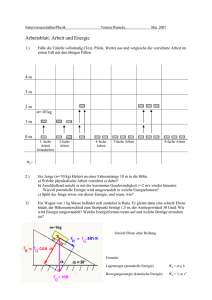
(PDF: 706,62 kB)

Vorwort
Die Bedeutung naturwissenschaftlicher Kenntnisse als Grundlage für technisches Verständnis
wird von vielen Seiten immer wieder betont: von
der Wirtschaft, der Politik, den Universitäten. Im
neuen Lehrplan für die HAK kommt die Wichtigkeit entsprechender Kenntnisse auch für Handelsakademiker zum Ausdruck.
Dieses Lehrbuch vermittelt einen Überblick über
die Grundlagen der Physik und ihre Anwendungsgebiete.
Die Neubearbeitung beschränkt sich auf das Wesentliche.
Der Stoff ist knapp zusammengefasst – das Buch
direkt zum Lernen geeignet. Mitschreiben beschränkt sich auf zu erarbeitende Zusammenhänge. Die Unterrichtszeit kann zum Lernen und
Verstehen genutzt werden.
Grob gibt es folgende Bereiche, die sich an den
Lehrplan anlehnen:
䉯 Einleitung – Grundlagen (Kap. 1–2)
䉯 Mechanik (Kap. 3–7)
䉯 Elektrizität und Magnetismus (Kap. 8–12)
䉯 Energie (Kap. 13–18)
䉯 Schwingungen und Wellen (Kap. 19–24)
䉯 Mikrokosmos und Makrokosmos (Kap. 25–30)
䉯 Erweiterung und Vertiefung (Kap. 31–40)
Jedes Kapitel umfasst etwa 4 bis 6 Seiten. Der
Stoffumfang ist für eine Unterrichtswoche gedacht. Den Basislehrstoff decken die ersten
30 Kapitel ab. Für die verbleibende Zeit können
entsprechende Kapitel aus dem Erweiterungslehrstoff gewählt oder das eine oder andere vertieft
werden.
Der Stoff wird knapp und übersichtlich präsentiert. Am Ende gibt es eine Zusammenfassung
der wesentlichen Inhalte. Das erleichtert das Lernen. Durchgerechnete Beispiele wird es nur dort
geben, wo die Rechnungen auch für die Praxis
relevant sind, zum Beispiel einfache Bewegungsaufgaben, elektrische Leistung, Energieverbrauch,
Wärmedämmung.
Zu den einzelnen Teilen im Detail:
Mechanik
Aus den alltäglichen Erfahrungen sind Schüler
mit der klassischen Mechanik vertraut. Schon
von Kindesbeinen an lernt man sich ihren Gesetzen entsprechend zu bewegen: Laufen, hinfallen,
zusammenstoßen, Bälle werfen usw. Man kennt
Ursachen und Wirkungen (Kräfte). Durch sportliche Aktivitäten und den Straßenverkehr wird
diese Erfahrung noch erweitert. Dieser Erfahrungsschatz der Schüler wird bei der Erarbeitung
physikalischer Gesetze auch genutzt. In der Mechanik wird recht genau auf entsprechende Zusammenhänge eingegangen (auch mathematisch)
und es werden Beispiele angeboten. Diagramme
werden erarbeitet und gedeutet.
In anderen Abschnitten werden mathematische
Zusammenhänge nicht mehr im Detail erarbeitet.
Physikalische Gesetze werden nur auf wesentliche Formeln beschränkt, die in wirtschaftlichen
Berufen sowie im Alltag von Bedeutung sind.
Elektrizität und Magnetismus
Elektrizität ist wohl der wichtigste und vielseitigste Energieträger. Deshalb sind Kenntnisse auf
diesem Gebiet wesentlich. Auch die Lehrplanforderung nach dem Verständnis der Funktionsweise
der in den Übungsfirmen eingesetzten technischen Geräte wird hier grundlegend abgedeckt.
Energie
In diesen Kapiteln wird die Energie in all ihren
Erscheinungsformen umfassend dargestellt.
Energie, Energieerhaltung, Energieversorgung,
Energieumwandlung sind jene Bereiche, die das
Zusammenleben und den Fortschritt der Menschen am meisten bestimmen und in Zukunft
wahrscheinlich immer mehr bestimmen werden.
Auch wirtschaftliche Überlegungen im Zusammenhang mit Energieverbrauch und -erzeugung
kommen zur Sprache. Formen alternativer Energiegewinnung werden ebenfalls vorgestellt.
6
Vorwort
Schwingungen und Wellen
Erweiterung und Vertiefung
Während sich die Mechanik des Buches vor allem mit der fortschreitenden Bewegung befasst,
steht hier die Bewegung in der Nähe eines Ortes
im Mittelpunkt. Und diese Grundlagen dienen
zum Verständnis der Energie- und Informationsübertragung. Es werden mechanische und elektromagnetische Phänomene behandelt.
Diese Kapitel behandeln die Themen Universum,
Relativitätstheorie, Rotation, Impuls, Hydround Aeromechanik, Akustik, Optik, Gasgesetze,
Elektronik, Laser und Erdatmosphäre.
Mikrokosmos und Makrokosmos
Kenntnisse aus der Chemie im 1. Jahrgang über
den Aufbau und das Zusammenwirken von Atomen werden hier um physikalische Aspekte erweitert. Problematiken der künstlichen Radioaktivität und des Strahlenschutzes sowie der Kernenergie werden hier aufgegriffen.
http://physikbuch.at
Um das Buch schlanker zu machen wurden einige
Teile auf eine eigene Website ausgelagert. Dort
werden zusätzliche, auf das Buch abgestimmte
Materialien zur Verfügung gestellt. Diese Aufgaben, Beispiele, Unterlagen und Arbeitsanregungen unterstützen die Wiederholung, Vertiefung
und Festigung des Lehrstoffs. Es ist sowohl individuelle Arbeit der SchülerInnen am Computer
als auch die Verwendung im Unterricht möglich.
3. Geschwindigkeit
Als Bezugssystem ist im Prinzip jeder andere
Körper geeignet. Sehr oft wird die Erde bzw. die
unmittelbare Umgebung verwendet.
Wenn sich der Ort, an dem sich ein Körper befindet, mit der Zeit ändert, so spricht man von einer
Bewegung des Körpers. Die Lehre von der Bewegung nennt man Kinematik. Zum Beschreiben
von Bewegungen sind Angaben über die beiden
Größen Ort und Zeit nötig.
3.1 Österreichrundfahrt
Die 4. Etappe der Österreich-Rundfahrt führte
am 10. Juni 2004 von Bad Gastein über den
Großglockner nach Lienz (148 km). Es gewannen die beiden Österreicher Gerrit Glomser und Andreas Matzbacher in 3:57:20. Das
entspricht einer mittleren Geschwindigkeit
von 37,42 km/h. Was für den Physiker alles
zur genauen Definition der Geschwindigkeit
gehört, erfährt man in diesem Kapitel.
3.3 Boot auf einem Fluss
Auch die Angabe des verwendeten Bezugssystems ist wesentlich: Die Geschwindigkeit eines
Bootes auf einem Fluss ist erst dann aussagekräftig, wenn wir zusätzlich erfahren, ob sie relativ
zum Wasser oder relativ zum Ufer zu verstehen ist.
Zur Beschreibung einer Bewegung genügt es, die
Bahnkurve des Körpers und die zeitliche Abfolge
seiner Lage auf dieser Bahnkurve zu kennen.
3.1 Der Begriff der Bewegung
Um den Ort eines Körpers angeben zu können,
braucht man Aussagen wie „auf dem Tisch“ oder
„in der rechten hinteren Ecke des Zimmers“ oder
„auf der Westautobahn bei km-Stein 152“ oder
ähnliches. Der Ort eines Körpers lässt sich also
nur unter Bezug auf den Ort eines anderen angeben, man benötigt ein Bezugssystem.
3.4 Bahnkurve einer Bewegung mit Durchgangszeiten in s
Das entsprechende Weg-Zeit-Gesetz kann in mathematischer Form als Bewegungsgleichung, in
Form eines Diagramms oder auch in einer Tabelle angegeben werden.
3.2 Wenn bei einem Unfall auf der Autobahn ein Hubschrauber benötigt wird, so orientiert sich der Pilot an großen Schildern mit der Angabe des „Autobahnkilometers“.
3.5 Auszug aus einem Fahrplan der ÖBB
3. Geschwindigkeit
3.2 Gleichförmig geradlinige
Bewegung
Ein PKW kommt auf der geraden Straße in regelmäßigen Zeitabständen an aufeinander folgenden Markierungen vorbei.
13
Diesen konstanten Wert nennt man die Geschwindigkeit v des Körpers. Der Ablauf der Bewegung ist durch Angabe dieser Größe eindeutig
beschrieben. Ihre Einheit wird aus den Basiseinheiten der Länge und der Zeit abgeleitet:
Größe
Formelzeichen
v
Geschwindigkeit
Einheit
Abkürzung
Meter pro Sekunde
3.6 Gleichförmige Bewegung eines PKW
Das Weg-Zeit-Diagramm
m/s
Definition
Geschwindigkeit=
Weg
Zeit
v=
∆s
∆t
weitere Einheiten
1 km/h=3,6 m/s
Größenordnungen für Geschwindigkeiten in m/s
3.7 Weg-Zeit-Diagramm der gleichförmigen Bewegung
des PKW
Abb. 3.7 zeigt die Bewegung des PKW aus
Abb. 3.6 in einem Diagramm. Der zurückgelegte
Weg s ist zur verstrichenen Zeit t direkt proportional, die grafische Darstellung ergibt eine Gerade. Je größer die Geschwindigkeit, desto steiler
ist diese Gerade. Eine waagrechte Gerade würde
bedeuten, dass der PKW steht.
10-6
1
10
102
103
3.104
3.108
Gletscher
Fußgänger
Radfahrer
Formel-I-Rennwagen
Überschallflugzeug
Erde um Sonne
Licht
Aus der Definitionsgleichung für die Geschwindigkeit erhalten wir durch Umformen für den
Weg bei gleichförmiger Bewegung
∆s=v.∆t
Die Geschwindigkeit
Wenn zwei Größen zueinander proportional sind,
so ist ihr Verhältnis konstant. Bildet man zu irgendeinem Zeitpunkt das Verhältnis „zurückgelegter Weg“ zu „verstrichene Zeit“, so ergibt sich
immer der gleiche Wert. Auch für beliebige Wegabschnitte ∆s erhält man für das Verhältnis
„Wegabschnitt ∆s“ zu „dafür benötigtes Zeitintervall ∆t“ immer den gleichen Wert. Der
griechische Buchstabe ∆ bezeichnet dabei eine
Differenz: ∆s=s2-s1 und ∆t=t2-t1.
und für die Zeit bei gleichförmiger Bewegung:
Eine Bewegung heißt gleichförmig, wenn ein
Körper in gleichen Zeitabschnitten ∆t gleich
lange Wegstrecken ∆s zurücklegt.
➔ Tipp: Vor Beginn einer Rechnung alle Angaben auf gleiche Einheiten, am besten SIEinheiten, umrechnen!
∆t=
∆s
v
BEISPIEL
Ein Motorrad legt in 5 s einen Weg von 30 m
zurück, ein PKW in 15 min einen Weg von
6,3 km. Welches Fahrzeug bewegt sich
schneller?
14
3. Geschwindigkeit
Motorrad:
gelegten Weg ist. Dies gilt auch allgemein für beliebige Geschwindigkeitskurven.
∆s M
30 m
=
=6 m/s
v M=
∆t M
5s
3.3 Die Geschwindigkeit als Vektor
PKW:
∆s PKW=6,3 km=6300 m
∆t PKW=15 min=15.60 s=900 s
vPKW=
∆s PKW
∆t PKW
=
6 300 m
=7 m/s
900 s
Antwort: Der PKW ist schneller.
Die mittlere Geschwindigkeit
Ein PKW fährt in 3 h von Wien nach Salzburg
(300 km). Wie groß ist seine Geschwindigkeit?
Die rasche Antwort (100 km/h) kann wohl nicht
für jeden Zeitpunkt der Bewegung richtig sein
(Anfahren, Bremsen, Überholen, Geschwindigkeitsbeschränkung bei Baustellen). Dieser Wert
kann nur ein Mittelwert sein:
Mittlere Geschwindigkeit=
Gesamtweg
Gesamtzeit
s
v=
t
Für viele Aufgabenstellungen ist die Angabe
der mittleren Geschwindigkeit ausreichend.
Das Geschwindigkeit-Zeit-Diagramm
Wenn die Geschwindigkeit konstant ist, ergibt
sich im v-t-Diagramm eine besonders einfache
Darstellung: eine Gerade parallel zur Zeitachse.
Bei manchen physikalischen Größen genügt die
Angabe von Zahlenwert und Einheit zur genauen
Charakterisierung. Bei Temperatur, Volumen,
Stoffmenge wäre speziell die Angabe einer Richtung sinnlos. Solche physikalische Größen heißen Skalare.
Bei der Geschwindigkeit ist nur die Angabe von
zum Beispiel 100 km/h nicht ausreichend. Für
den Bewegungsablauf ist es wesentlich, wohin
sich der Körper mit dieser Geschwindigkeit bewegt. Größen, für die ihre Richtung ein entscheidendes Merkmal darstellt, bezeichnet man als
Vektoren.
3.9 Vektoren
Der Vektor ist als eine Größe mit den Bestimmungsstücken Betrag, Richtung und Richtungssinn definiert.
Ein Vektor wird durch einen Pfeil dargestellt.
Die Länge des Pfeiles entspricht dabei dem Betrag in einem geeignet gewählten Maßstab:
3.10 Geschwindigkeitsvektoren
Der Geschwindigkeitsvektor des PKW in
Abb. 3.10 für 100 km/h wird durch einen Pfeil
dargestellt, der doppelt so lang ist wie der für den
LKW, der mit 50 km/h unterwegs ist.
3.8 Geschwindigkeit-Zeit-Diagramm der
gleichförmigen Bewegung des PKW
In Abb. 3.8 sieht man, dass die Fläche unter der
Geschwindigkeitskurve ein Maß für den zurück-
Bei einfachen Bewegungen längs einer Geraden
genügt es, den Richtungssinn durch das Vorzeichen des Geschwindigkeitsbetrages zu berücksichtigen:
3. Geschwindigkeit
15
t=
s
=0,857 h=51,4 min
v rel
Den Ort C der Begegnung errechnet
man z. B. aus der Bewegung des Zuges A
nach B:
AC=v1.t=68,6 km
Die grafische Lösung zeigt Abb. 3.13.
3.11 Bewegung mit Richtungsumkehr
Hier rollt eine Kugel mit konstanter Geschwindigkeit auf eine Mauer zu. Der zurückgelegte
Weg wächst linear mit der Zeit an. Ab dem Zeitpunkt t1, wird s wieder kleiner. Die Kugel rollt
offenbar zurück: sie hat beim Aufprall an der
Mauer zum Zeitpunkt t1 ihre Richtung umgekehrt, die Geschwindigkeit v ist jetzt negativ.
3.4 Relativgeschwindigkeit
3.13 Grafische Lösung einer Bewegungsaufgabe
Die grafische Darstellung der Zugbewegungen auf einer Strecke steht dem Fahrdienstleiter jedes Bahnhofs als Bildfahrplan zur Verfügung.
BEISPIEL
1
Zwischen zwei Orten A und B (Entfernung
120 km) verkehrt eine Eisenbahnlinie.
In A fährt um 9.10 Uhr ein Zug ab; Planankunft in B um 10.40 Uhr. Gleichzeitig
fährt in B ein Zug ab; Planankunft in A
um 11.10 Uhr. Wann und wo begegnen
die Züge einander?
3.12 Begegnung zweier Züge
v 1=
120 km
=80 km/h
1,5 h
v2=
− 120 km
=-60 km/h
2h
Die beiden Züge haben also die Relativgeschwindigkeit (Vorzeichen beachten!):
vrel=v1-v2=140 km/h
Sie brauchen daher bis zur Begegnung die
Zeit (es muss gemeinsam die Strecke von
120 km zurückgelegt werden!):
Zusammenfassung
䉯 Um den Ort eines Körpers genau anzugeben ist ein Bezugssystem notwendig.
䉯 Geschwindigkeit=
Weg
Zeit
v=
∆s
∆t
䉯 SI-Einheit der Geschwindigkeit: m/s
䉯 Es gilt: 3,6 km/h=1 m/s
䉯 Das Weg-Zeit-Diagramm für eine gleichförmige Bewegung ist eine Gerade. Ihr
Anstieg ist ein Maß für die Geschwindigkeit.
䉯 Der Flächeninhalt unter der Kurve im
Geschwindigkeit-Zeit-Diagramm gibt
den zurückgelegten Weg an.
䉯 Die Geschwindigkeit ist eine vektorielle
Größe mit Betrag, Richtung und Richtungssinn.
䉯 Für viele Anwendungen ist es ausreichend, wenn man mit der mittleren Geschwindigkeit rechnet.
14. Energieerhaltung
59
14. Energieerhaltung
Ein Stabhochspringer setzt seine Geschwindigkeit beim Anlauf über den Stab in Höhe
um.
Wird eine Feder mit der Federkonstanten D um
die Strecke s gespannt, so besitzt sie die
2
elastische Energie: Eelast=
D. s
2
Elektromagnetische Energieformen
Energie in elektrischer Form hat eine sehr große
Bedeutung. Sie kann sehr leicht transportiert und
gespeichert werden. Durch einfache Umwandlungen in andere Energieformen ist sie für vielfältigste Anwendungen geeignet.
Ein auf eine Spannung U geladener elektrischer
Kondensator mit der Kapazität C hat die
2
elektrische Energie: Eel=
C.U
2
14.1 Stabhochsprung
Kinetische, potentielle und elastische Energie kommt hier zum Tragen. Dass dabei aber
auch chemische und elektrische Energie sowie Wärme eine große Rolle spielen, zeigt
dieses Kapitel.
Oft werden mechanische Modelle herangezogen,
weil man sich elektrische Vorgänge dann leichter
vorstellen kann. So kann der geladene Kondensator mit einer gespannten Feder verglichen werden.
Fließt durch eine Spule mit der Induktivität L ein
Strom I, so beträgt die
14.1 Überblick über Energieformen
magnetische Energie: Emag=
Mechanische Energieformen
Die Mechanik ist aus dem Alltag vertraut und daher sind auch diese Energieformen leicht verständlich.
Abhängig von der Höhenlage h im Gravitationsfeld der Erde besitzt ein Körper mit der Masse m
die Lageenergie bzw.
potentielle Energie: Epot=m.g.h
Bewegt sich eine Masse m mit der Geschwindigkeit v, so beträgt die Bewegungsenergie bzw.
2
kinetische Energie: Ekin=
m. v
2
L. I 2
2
Diese Energie kann mit der kinetischen Energie
aus der Mechanik verglichen werden. Es handelt
sich auch hier um eine Energieform der Bewegung.
Wärme
Wärme ist die Energie der ungeordneten Bewegung der Moleküle eines Körpers.
Chemische Energie
Bei einem chemischen Prozess kommt es zu einer Stoffumwandlung – die Zusammensetzung
der Moleküle ändert sich. Ist der Energieinhalt
der Ausgangsstoffe kleiner als jener der Endprodukte, so wird für diesen Prozess Energie benö-
60
tigt. Im anderen Fall wird Energie meist in Form
von Wärme und Strahlung frei.
Heizwert
Als Heizwert H definiert man jene Wärmemenge Q, die bei vollständiger Verbrennung von
1 kg des Stoffes freigesetzt werden kann:
Q
H=
m
Nährstoffe
Bei Angaben zu Inhaltsstoffen von Nahrungsmitteln wird die Einheit Joule (manchmal auch noch
Kalorien) verwendet. Es handelt sich dabei um
jene Energie, die dem Körper beim Essen zugeführt wird. Sie wird biochemisch umgesetzt.
Strahlungsenergie
Lichtwellen (allgemein elektromagnetische Wellen) können Energie auch ohne Medium übertragen. Die Energie ist von der Frequenz abhängig.
Nukleare Energieformen
Kernenergie (auch Atomenergie) – durch Bindungskräfte zwischen den Kernbestandteilen
verursacht – kann seit Mitte des 20. Jahrhunderts
genutzt werden. Dabei spielt Masse als Energieform eine Rolle (Relativitätstheorie).
14.2 Energiesatz
Beim Herabfallen eines Körpers der Masse m
um die Höhe h sinkt seine potentielle Energie.
Gleichzeitig steigt aber seine Geschwindigkeit,
also hat er kinetische Energie gewonnen.
14. Energieerhaltung
Mit Hilfe der zeitfreien Gleichung sieht man leicht:
2
m⋅v
m
Ekin=
= .2.g.h=m.g.h=Epot
2
2
Die gewonnene kinetische Energie ist genau so
groß wie die verlorene potentielle Energie: Epot
ist in Ekin umgewandelt worden.
Der Energiesatz im abgeschlossenen
System
Wenn in einem System (ein oder mehrere Körper) nur innere Kräfte wirksam sind, es aber
nicht mit anderen Körpern der Umgebung in
Wechselwirkung treten kann, so nennt man es ein
abgeschlossenes System. Die Erde ist zum Beispiel für viele Zwecke ein solches System.
Kurz gesagt: In ein abgeschlossenes System greifen keine äußeren Kräfte ein. Die Gesamtenergie
(Summe aller Energieformen) in einem solchen
System wird also nicht durch Verrichtung von
Arbeit von bzw. nach außen verändert:
In einem abgeschlossenen System bleibt die
Gesamtenergie konstant.
Der Energiesatz im nicht abgeschlossenen
System
Wenn äußere Kräfte am System Arbeit verrichten, so bleibt die Gesamtenergie natürlich nicht
mehr konstant. Es gilt:
Die Änderung der Gesamtenergie ist gleich
der Arbeit der äußeren Kräfte.
∆Eges=WA
Dabei sind zwei Fälle möglich:
14.3 Energiesatz im nicht abgeschlossenen System
14.2 Umwandlung von Lageenergie in Bewegungsenergie
1. Die äußeren Kräfte verrichten Arbeit am
System, WA ist positiv: Es fließt Energie in das
System, die Energie des Systems nimmt zu.
14. Energieerhaltung
2. Das System verrichtet Arbeit gegen äußere
Kräfte. WA ist negativ: Es fließt Energie aus dem
System, die Energie des Systems nimmt ab.
14.3 Energieumwandlungen
An einzelnen Beispielen soll die Auswirkung des
Energiesatzes bzw. seine Anwendung gezeigt
werden. Bei vielen Vorgängen, bei denen andere
Energieformen „verschwinden“, wird Wärme
„erzeugt“. Wärmeenergie ist an jeder Energieumwandlung beteiligt.
Kugeltanz
Ein Gummiball fällt senkrecht auf eine harte
Oberfläche. Beim Herabfallen wird potentielle
Energie in kinetische umgewandelt, diese beim
Aufprall vorübergehend in elastische und wieder
zurück in kinetische. Beim Hochspringen wird
die kinetische Energie wieder in potentielle umgewandelt. Wenn der Aufprall völlig elastisch erfolgt, so erreicht der Ball exakt wieder die Aus-
61
gangshöhe h, der Vorgang wiederholt sich periodisch.
Erfolgt der Stoß nicht völlig elastisch
(Abb. 14.4), so geht jedesmal ein bestimmter
Teil der vorhandenen Energie für die Bewegung
verloren (wird in Verformungsarbeit, Schall,
Wärme umgewandelt). Der Ball kann dann die
Ausgangshöhe nicht mehr erreichen.
Galileisches Hemmungspendel
Beim Herabschwingen des ausgelenkten Pendelkörpers wird potentielle Energie in kinetische
umgewandelt. Am tiefsten Punkt der Bahn ist nur
mehr Ek vorhanden. Beim Hochsteigen wird sie
wieder in Ep umgewandelt. Ohne Reibung (Luftwiderstand) erreicht das Pendel wieder die Ausgangshöhe h, auch wenn man durch einen Stab
eine andere Bahn erzwingt.
14.5 Galileisches Hemmungspendel
Maxwellsches Rad
Beim Drehen des Rades werden die Aufhängungsfäden auf der Welle aufgewickelt, das Rad
wird gehoben, es wird Hubarbeit verrichtet und
das Rad erhält Lageenergie. Beim Loslassen
„fällt“ das Rad unter Abwicklung der Fäden nach
unten, die Lageenergie wird in Bewegungsenergie umgewandelt (hier überwiegend Bewegungsenergie der Rotation!). Am tiefsten Punkt hat das
Rad nur Bewegungsenergie – es dreht sich weiter, die Fäden werden in umgekehrter Richtung
wieder aufgewickelt, das Rad steigt wieder hoch
usw. Ein Jo-Jo funktioniert nach dem gleichen
Prinzip.
14.4 Springender Ball
Auch diese Bewegung würde ohne Reibung nicht
zum Stillstand kommen. Bei genauer Betrachtung muss man noch ergänzen, dass nach Abwicklung des Fadens noch etwas Translationsenergie vorhanden ist, die eine Dehnung des Fa-
62
14. Energieerhaltung
Glühlampe
Elektronen stoßen mit den Atomen im Metallgitter zusammen. Dadurch erhitzt sich der Draht
und beginnt zu glühen. Es entsteht haupsächlich
Wärmeenergie und nur sehr wenig Strahlungsenergie im sichtbaren Bereich des Lichts.
Bremsen
14.6 Maxwellsches Rad
dens bewirkt und bis zum tatsächlich tiefsten
Punkt (vorübergehend!) in elastische Energie
umgewandelt wird.
Stabhochsprung
Die komplexen Energieumwandlungen beim
Stabhochsprung sind in Abb. 14.7 dargestellt.
Beim Bremsen eines Fahrzeugs wird die kinetische Energie vollständig in Wärme umgewandelt. Diese Wärmeenergie muss von den Bremsen abgeführt werden, da es sonst zu einer Beeinträchtigung der Funktion kommen kann. Bei
elektrisch betriebenen Fahrzeugen kann man
auch eine Bremswirkung erzielen, indem man
von Motor- in Generatorbetrieb umschaltet und
aus der Bewegungsenergie Strom erzeugt.
Solarzelle
Mit Hilfe von Solarzellen kann Sonnenenergie
direkt in elektrische Energie umgewandelt werden (siehe dazu Abschnitt 38.3).
Auto
Wärmeenergie, die durch Verbrennung erzeugt
wird, wird über Wärmekraftmaschinen in mechanische Energie umgewandelt.
Zusammenfassung
14.7 Stabhochsprung
Damit mechanische Arbeit erbracht werden kann,
muss dem Körper (chemische) Energie in Form
von Nahrung zugeführt werden. Beruhend auf
den Bindungskräften zwischen den Molekülen in
den Muskeln ist diese chemische Energie letztlich
wieder elektrischer Natur. Weiters wird bei diesem Vorgang auch noch Wärmeenergie frei.
Staukraftwerk
Die potentielle Energie des Wassers in einem
Stausee wird im Druckrohr in kinetische Energie
umgewandelt. Das rasch fließende Wasser treibt
einen Generator an, der über Induktion elektrische Energie erzeugt. Auch hier gibt es Verluste
in Form von Wärme.
䉯 Energie tritt in allen Bereichen in verschiedenen Formen in Erscheinung: mechanisch, elektromagnetisch, chemisch,
als Wärme, als Strahlung, in Atomen und
Massen.
䉯 Energiesatz: In einem abgeschlossenen
System bleibt die Gesamtenergie erhalten.
䉯 Energie kann weder verloren gehen noch
erzeugt werden.
䉯 Jede Wechselwirkung zwischen Körpern
steht mit Energieumwandlungen in Zusammenhang. Es gibt viele Auswirkungen bzw. Anwendungen.
䉯 Bei vielen Vorgängen, bei denen andere
Energieformen „verschwinden“, wird
Wärme „erzeugt“. Wärmeenergie ist an
jeder Energieumwandlung beteiligt.