Laboratorium für Grundlagen Elektrotechnik

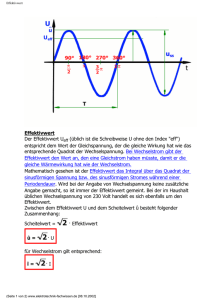
Fachhochschule Köln
University of Applied Sciences Cologne
Fakultät 07:
Informations-, Medien- & Elektrotechnik
Institut für Elektrische Energietechnik
Laboratorium für
Grundlagen Elektrotechnik
Versuch 4
4.1 Mittelwerte bei Wechselstrom
4.2 Addition von Wechselspannungen
4.3 Spannungszeigerdiagramm
4.4 Blindleistungskompensation
Gruppe:
Versuchstermin:
Name:
Abgabetermin:
Vorname:
Matr.-Nr.
Protokollführer:
Teilnehmer:
Teilnehmer:
Teilnehmer:
Teilnehmer:
Teilnahmetestat:
Fachhochschule Köln
Institut für Elektrische Energietechnik
Anerkennungstestat:
1
GE-Labor
Stand : 03.2012
Grundlagen
Ein sinusförmiger Wechselstrom kann durch verschiedene Größen beschrieben
werden. Für Isolationszwecke ist z.B. der Scheitelwert (Amplitude) von Interesse.
Für die meisten Anwendungen ist der Effektivwert ausschlaggebend.
Der Stromeffektivwert entspricht dem Wert eines konstanten Gleichstromes, der in
einem gleichen Widerstand in derselben Zeit zur gleichen Erwärmung führt.
Es gilt:
T
Arithmetischer Mittelwert: I =
1
i (t ) dt
T ∫0
Effektivwert
~
I =
Gleichrichtwert:
I =
T
1 2
i (t ) dt
T ∫0
T
1
i (t ) dt
T ∫0
Einige Messgeräte stellen aufgrund ihres physikalischen Aufbaus den
Gleichrichtwert dar. Um dennoch den Effektivwert bei sinusförmigen Messgrößen
darzustellen wird die Anzeige mit dem so genannten Formfaktor multipliziert.
~
I
fi =
I
Formfaktor:
Versuchsdurchführung
4.1 Mittelwerte bei Wechselstrom
RV
~ 50Hz
I1
I2
I3
Drehspulmeßgerät
Dreheisenmeßgerät
Digitales
Messgerät
In
b)
a)
EinweggleichBrückenschaltung richtung
~
+
~
Ein sinusförmiger Wechselstrom mit der Frequenz f=50Hz wird gleichgerichtet
(Einweg- und Zweiweggleichrichtung) und speist einen Akkumulator (Akku).
Verschiedene Strommessungen von mehreren in Reihe geschalteten Amperemetern
ergeben unterschiedliche Werte, obwohl sie alle vom selben Strom durchflossen
werden.
a) Der Akku ist mit der Brückenschaltung (Zweiweggleichrichtung) zu laden.
1. Erklären Sie die unterschiedlichen Messwerte.
2. Tragen Sie die unterschiedlichen Messwerte in eine Tabelle ein.
3. Welchen Stromverlauf durch die Messgeräte und den Akku erwarten Sie?
Skizzieren Sie die Verläufe über mindestens zwei Perioden als Funktion der
Zeit.
Fachhochschule Köln
Institut für Elektrische Energietechnik
2
GE-Labor
Stand : 03.2012
b) Der Akku ist nun mit der Einweggleichrichtung zu laden.
1. Erklären Sie die unterschiedlichen Messwerte
2. und tragen Sie wie unter Punkt a) die Messwerte in die Tabelle ein.
3. Skizzieren Sie die erwarteten Stromverläufe als Funktion der Zeit (wie in
Punkt a).
4.2 Addition von Wechselspannungen
a) bei Überlagerung mit Gleichspannung
=
U1
U1
U
U2
~ 50Hz
U2
Für den Effektivwert der überlagerten Spannung aus Gleichspannung und
sinusförmiger Wechselspannung gilt:
U
û2
U1
t
1 2
u dt
u = U1 + u2 = U1 + û2 ⋅ sin ωt
T ∫
1
2
U 2 = ∫ (U1 + û2 sin ωt ) dt
T
1
U 2 = ∫ U12 + û2 sin2 ωt + 2 ⋅ U1 ⋅ û2 sin ωt dt
T
1
1 2
1
U 2 = ∫ U12 dt +
û2 sin2 ωt dt +
2 ⋅ U1 ⋅ û2 sin ωt dt
∫
T
T
T∫
U2 =
(
)
Gleichanteil
U2 =
⇒
U12
.
2 U1 x arithmetischer Mittelwert
Effektivwert
+
U 22
+
0
U = U12 + U 22
Fachhochschule Köln
Institut für Elektrische Energietechnik
3
GE-Labor
Stand : 03.2012
Eine Glühlampe soll mit einer Reihenschaltung einer Gleich- und einer
Wechselspannungsquelle bei ihrer Nennleistung betrieben werden. Die
Gleichspannung U1 und die Nennspannung der Glühlampe sind gegeben.
1. Berechnen Sie die Größe der sinusförmige Wechselspannung U2 so, dass der
Effektivwert der Spannung an der Glühlampe der Nennspannung entspricht.
2. Stellen Sie die berechnete Wechselspannung U2 in der Schaltung ein und notieren
Sie die Spannung U an der Glühlampe.
b) bei gleicher Frequenz
L1
L2
L3
N
U1
U
U2
Für die Addition von Spannungen gleicher Frequenz gilt
U = U12 + U 22 + 2 ⋅ U1 ⋅ U 2 ⋅ cos ϕ
ϕ ist der Winkel zwischen U1 und U2
1. Für beide Schalterstellungen sind die Effektivwerte zu messen und der jeweilige
Winkel ϕ zwischen den beiden Spannungen U1 und U2 zu berechnen.
2. Veranschaulichen Sie an einem maßstäblichen Zeigerdiagramm, in welchem
Bereich die Gesamtspannung U verändert werden kann bei betragsmäßig
konstanten Werten für U1 und U2, jedoch veränderlichen Phasenverschiebungen
zwischen den beiden Spannungen.
3. Zeigen Sie graphisch um welchen größten Winkel U gegenüber U1 verschoben
sein kann.
Fachhochschule Köln
Institut für Elektrische Energietechnik
4
GE-Labor
Stand : 03.2012
4.3 Spannungszeigerdiagramm
US
UR
UC
I
Ls
RS
R
C
Spule
U
Spule 1:
Spule 2:
N = 250
N = 1000
Bei einer Reihenschaltung von einem Widerstand, einer Spule und einem
Kondensator sind aus den Betragsmessungen der Teilspannungen und des Stromes
die Impedanzen aller Bauelemente sowie die Gesamtimpedanz zu bestimmen.
a) 1. Zeichnen Sie in einem geeigneten Maßstab die Zeigerdiagramme die
beiden unterschiedlichen Spulen. Es muss gelten U = UR + US + UC.
2. Geben Sie den Phasenwinkel der jeweiligen Spulenspannung US
gegenüber dem Strom I an.
b) Berechnen Sie die Induktivitäten LS und die ohmschen Widerstände RS der
Spulen.
4.4 Blindleistungskompensation
I
P
RL
R
U~
U
C
L
Motor
Ein Wechselstrommotor wird (im Schaltbild dargestellt durch die Reihenschaltung
von R und L) am Wechselstromnetz betrieben.
a) Nehmen Sie die Messwerte bei geöffnetem Schalter auf. Berechnen Sie die
Scheinleistung S, die Wirkleistung P, die Blindleistung Q und cos ϕ.
b) Schließen Sie den Schalter und führen Sie die Berechnung wie unter a) aus.
c) Der Widerstand RL steht stellvertretend für Leitungswiderstände in der
Zuleitung.
1. Wie groß sind die Verluste im Widerstand RL, wenn der Schalter geöffnet
ist?
2. Um wie viel Prozent verringern sich die Verluste im Widerstand RL, wenn
der Kondensator C hinzu geschaltet wird?
Fachhochschule Köln
Institut für Elektrische Energietechnik
5
GE-Labor
Stand : 03.2012