Ladungen und Elektrische Felder

10. Elektrizitätslehre
10.1 Einleitung
Einleitung
Die wesentlichen Entwicklungen der Elektrizitätslehre fanden in der ersten Hälfte des 19. Jahrhunderts statt und kulminierten
in den sogenannten 4 Maxwellgleichungen (1856), die sowohl als Differentialgleichungen als auch als Integralgleichungen
formuliert werden können.
Aus diesen 4 Gleichungen können (zusammen mit Materialgleichungen, die die Materialien beschreiben) alle elektrodynamischen Phänomene abgeleitet werden.
Die folgenden Abschnitte enthalten eine (Ultra)kurzzusammenfassung wesentlicher elektromagnetischer Sachverhalte.
Im Abschnitt "Elektrostatik: Ladungen und Elektrische Felder" wird untersucht wie statische Ladungen ein konstantes elektrisches Feld erzeugen und welche Kräfte durch elektrische Felder auf Ladungen ausgeübt werden.
Im Abschnitt "Magnetostatik: Strom, Magnetisches Feld" wird untersucht wie statische Ströme ein konstantes magnetisches
Feld erzeugen und welche Kräfte durch magnetische Felder auf bewegte Ladungen und Ströme ausgeübt werden.
Im Abschnitt "Elektrodynamik: Induktion" wird untersucht wie Spannungen und Ströme durch Bewegen eines Leiters in
einem magnetischen Feld oder durch Ändern des magnetischen Flusses in einer Leiterschleife induziert werden können.
Zum Abschluss werden im Abschnitt "Stromkreise" noch einfache Stromkreise untersucht.
10.2 Elektrostatik: Ladungen und Elektrische Felder
Ladungen
Die Ladung ist eine elementare Eigenschaft von Elementarteilchen. Die Ladung kann positiv, null oder negativ sein. Die in den
Atomen vorkommenden Elementarteilchen Proton, Neutron und Elektron haben die Ladung +e, 0 und -e, wobei e die sogenannte
elektrische Elementarladung mit einem Wert von e = 1.602177 * 10-19 C darstellt.
Noch kleinere Ladungen kommen in der Natur in Quarks vor aus denen das Proton und das Neutron zusammengesetzt sind.
Die Quarks können Drittel(Elementar)ladungen haben (Up Quark + ÅÅÅÅ23 e, Down Quark + ÅÅÅÅ13 e). Ein einzelnes Quark ist jedoch
nicht beobachtbar.
Die Ladung hat das Formelzeichen Q und die SI-Einheit: @QD = Amperesekunde HAsL = Coulomb HCL
Die Ladungen sind die Ursache der elektromagnetischen Kraft. Gleich geladene Teilchen stossen sich ab, ungleich geladene Teilchen
ziehen sich an.
Es gilt im Atom:
† ein Atom besteht aus negativ geladenen Elektronen und einem positiv geladenen Kern;
diese anziehende Kraft und die Regeln der Quantenmechanik führen auf die verschiedenen möglichen Zustände des
Atoms (Grundzustand, angeregte Zustände, Ionisierung etc.)
2
† der Atomkern besteht aus positiv geladenen Protonen und neutralen Neutronen; die abstossenden Kräfte zwischen den
Protonen werden balanciert durch die anziehende starke Kraft im Kern.
Es gilt in einem Festkörper:
† Bei vielen Nichtleitern (Bernstein, Glas, Hartgummi u.a.) kann durch Reibung die Oberfläche elektrisch geladen werden.
Der Oberfläche werden bei diesem Vorgang Elektronen entzogen oder zugeführt.
† Elektronenmangel bedeutet, der Körper ist positiv geladen;
† Elektronenüberschuss bedeutet, der Körper ist negativ geladen;
† Bei Leitern sitzen die überschüssigen Ladungen stets an der Oberfläche. Das Innere ist ladungs- und feldfrei. Die Verteilung der Ladung ist ungleich. An stärker gekrümmten Stellen sitzen sie dichter. An Spitzen und Kanten können sie so
dicht sitzen, dass sie die Luft ionisieren und den Körper verlassen können.
Eine Ladung Q erzeugt ein elektrisches Feld
Um die anziehenden und abstossenden Kräfte zwischen Ladungen zu verstehen und zu beschreiben bedient man sich des
i Ex @x, y, zD yz
z
÷” jjjj
Modells eines elektrischen Feldes: E = jj E y @x, y, zD zzzz
j
z
k Ez @x, y, zD {
Für jeden Ort Hx, y, zL ist das elektrische Feld ein Vektor (d.h. es hat eine Grösse und eine Richtung) und hat somit drei
Komponenten HEx , E y , Ez L.
Bei der graphischen Visualisierung eines solchen Vektorfeldes werden an ausgewählten Positionen Pfeile eingezeichnet,
wobei die Länge der Pfeile ein Mass für die Stärke des elektrischen Feldes und die Richtung der Pfeile die Richtung des
elektrischen Feldes für diese Positionen angibt.
Ein elektrisches Feld lässt sich auch mit Hilfe von Feldlinien beschreiben. Dabei starten die Feldlinien von den positiven
Ladungen und enden bei negativen Ladungen oder im Unendlichen. Die Tangenten an die Feldlinien liefern die Richtung des
elektrischen Feldes, die Dichte der Linien ist ein Mass für die Stärke des elektrischen Feldes.
Je nach Verlauf der Feldlinien nennt man das Feld radial, homogen (bei parallelen Feldlinien) oder inhomogen (bei nichtparallelen Feldlinien).
Radiales Feld
Homogenes Feld
Inhomogenes Feld
Q
1
Eine Punktladung Q erzeugt ein radiales elektrisches Feld, das (im Vakuum) im Abstand r die Feldstärke: E = ÅÅÅÅÅÅÅÅ
ÅÅÅÅÅ ÅÅÅÅ
ÅÅ hat. e0 ist die
4 p e0 r2
-12 C
elektrische Feldkonstante und hat den Wert e0 = 8.85419 * 10
ÅÅÅÅ
ÅÅÅÅÅÅ
Vm
3
Ein elektrisches Feld übt eine Kraft auf eine Ladung Q aus.
Die elektrische Feldstärke E ist das Verhältnis der auf eine (kleine, das Feld nicht verändernde, positive) Ladung im elektrischen Feld
÷ ” F÷ ”
Å.
wirkenden Kraft zur Grösse dieser Ladung oder kurz gesagt die Kraft pro Ladungseinheit: E = ÅÅÅÅÅ
Q
N
N
Die SI Einheit der elektrischen Feldstärke: @ED = ÅÅÅÅ
Å J = ÅÅÅÅ
ÅÅ Å
C
As
W=A V V N
= ÅÅÅÅWÅÅÅÅsÅÅ N
= ÅÅVmÅÅÅÅ
In inhomogenen Feldern ist die Kraft örtlich verschieden.
Für eine positive Ladung wirkt die Kraft entlang der Feldlinien, für negative Ladungen in umgekehrter Richtung
Kraft auf Ladungen im elektrischen Feld
Es gilt somit:
÷”
÷”
F = †F § = Q †E § = Q E
Betrag der Kraft F auf eine Ladung Q im elektrischen Feld der Feldstärke E .
Felder, die senkrecht zur Zeichenfläche verlaufen, werden durch Punkte (aus der Zeichenfläche heraus) bzw. X (in die
Zeichenfläche hinein) eingezeichnet:
Feld aus der Zeichenfläche heraus
Feld in die Zeichenfläche hinein
Eine Ladung Q1 übt somit eine Kraft F auf eine zweite Ladung Q2 aus.
Wir haben gesehen, dass eine (erste) Ladung Q1 ein elektrisches Feld erzeugt. Dieses elektrische Feld übt eine Kraft auf eine
zweite Ladung Q2 aus. Zusammengenommen: eine Ladung übt auf eine zweite Ladung eine Kraft aus. Und gemäss dem
Prinzip " Actio = Reactio " übt diese zweite Ladung die gleich grosse Kraft in umgekehrter Richtung auf die erste Ladung aus.
Q1 Q2
1
F = ÅÅÅÅÅÅÅÅ
ÅÅÅÅÅ ÅÅÅÅÅÅÅÅ
ÅÅÅÅÅÅÅ
4pe
r2
0
Kraft F zwischen zwei Ladungen Q1 und Q2 , die sich im Abstand r voneinander
befinden.
4
Kraft zwischen zwei Ladungen
Elektrisches Potenzial
Die Verschiebung einer Ladung Q im elektrischen Feld E vom Punkt A zum Punkt B erfordert (oder liefert) die Arbeit
B ÷ ” ÷÷÷”
B ÷ ” ÷÷÷”
W = Ÿ A F ds = Q Ÿ A E ds = Q fA,B .
Spannung zwischen zwei Punkten im elektrischen Feld
B ÷ ” ÷÷÷”
Das Integral f A,B = Ÿ A E ds wird als elektrische Potenzialdifferenz oder elektrische Spannung U bezeichnet und stellt die für die
Verschiebung pro Ladungseinheit zu leistende Arbeit dar:
W
U = f A,B = ÅÅÅÅ
ÅÅ
Q
J
Die Spannung U hat die SI Einheit: @UD = @f A,B D = ÅÅÅÅÅ
= Volt HV L.
C
Festkörper in einem elektrischen Feld
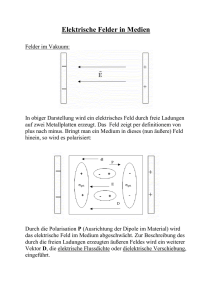
Stoffe, die in ein elektrisches Feld gebracht werden, verändern die elektrische Feldstärke im Stoff auf unterschiedliche Weise.
Influenz bei Leitern
Wenn sich ein Leiter in einem elektrischen Feld befindet, dann verteilen sich die (freien) Ladungsträger des Leiters so an der
Oberfläche, dass sie das äussere Feld kompensieren und somit im Inneren des Festkörpers die elektrische Feldstärke E gleich
0 ist. Weiters haben die von aussen auf der Oberfläche endenden Feldlinien nur Komponenten senkrecht zur Oberfläche.
Polarisation bei Nichtleitern
Wenn sich ein nichtleitender Stoff (Dielektrikum) in einem elektrischen Feld befindet, so werden die positiven Kerne entlang
des elektrischen Feldes und die Elektronen in der Atomhülle in die Gegenrichtung verschoben. Dem ursprünglichen Feld ohne
Dielektrikum E0 wirkt ein ED der Dipolmoleküle entgegen. Der Betrag des Gesamtfelds E = E0 - ED wird deshalb verkleinert.
5
Influenz bei Leitern
Dielektrische Polarisation
(Faraday'scher Käfig)
(D gleich,E schwächer)
Elektrische Flussdichte D, Permittivität
Ein elektrisches Feld kann wie gezeigt aus zwei Blickwinkeln betrachtet werden:
† Blickwinkel Ursache: Ladungen erzeugen ein elektrisches Feld
† Blickwinkel Wirkung: ein elektrisches Feld übt eine Kraft auf eine Ladung aus
Für jeden dieser beiden Blickwinkel kann eine entsprechende Grösse für das elektrische Feld verwendet werden. Zur Beschreibung der Kraftwirkung verwendet man die oben diskutierte elektrische Feldstärke E. Zur Beschreibung des Feldes aus der
Sicht der vorkommenden freien Ladungen verwendet man die sogenannte elektrische Flussdichte D.
÷÷”
Die elektrische Flussdichte D ist eine vektorielle, physikalische Grösse, deren Betrag durch die freien Ladungen oder die Ladungen an
der Oberfläche eines Leiters (der sogenannten Flächenladungsdichte: D = ÅÅÅÅQAÅ ) bestimmt wird.
C
N
VN
Die SI Einheit der elektrischen Flussdichte: @DD = ÅÅÅÅ
ÅÅÅÅ H = ÅÅÅÅ
ÅÅÅÅ = ÅÅÅÅ
ÅÅÅÅÅÅ L = ÅÅÅÅVmÅ
m2
As
Ws
Im Vakuum sind E und D (bis auf die Konstante e0 ) identisch. In einem Dielektrikum treten Ladungsverschiebungen bzw.
Polarisationen P auf, deren Grösse durch die Permittivität beschrieben wird. Die elektrische Flussdichte wird nur durch die
freien Ladungen bestimmt, während die elektrische Feldstärke (d.h. die Kraftwirkung) durch die Polarisationen verändert
wird. Die beiden physikalischen Grössen stehen in folgendem Zusammenhang.
D = e0 E
Elektrische Flussdichte D im Vakuum.
D = er e0 E
Elektrische Flussdichte D in einem Körper mit der Permittivitätszahl eR .
e = er e0
Permittivität (alt: Dielektrizitätskonstante)
er =
E0
ÅÅÅÅ
ÅÅÅÅ
E
Permittivitätszahl des Stoffs ( Ø Tabellen)
e0 =
8.85419 * 10-12 ÅÅmFÅÅÅÅ
elektrische Feldkonstante
Wie man Tabellen entnehmen kann ist für Stoffe die Permittivitätszahl e > 1, für Luft e º 1.0006 (trocken und bei Normalbedingungen) und e = 1 für Vakuum.
Plattenkondensator
Ein Kondensator ist ein wichtiges Element in elektronischen Schaltkreisen. Wenn eine Spannung U an diesem Bauteil anliegt,
vermag es eine bestimmte Ladungsmenge Q zu speichern. Je höher die Spannung U ist desto grösser Q. Die Proportionalitätskonstante wird Kapazität genannt und ist folgendermassen definiert:
6
Q
Die Kapazität C gibt an wieviel Ladung Q ein Kondensator bei einer bestimmten Spannung U aufnehmen kann: C = ÅÅÅÅ
Å.
U
Sie hat das Formelzeichen C.
As
Die SI-Einheit der Kapazität ist: @CD = ÅÅÅÅ
ÅÅ Å = ÅÅVCÅÅÅÅ = F
V
Im Folgenden wollen wir eine Realisierung eines Kondensators, einen sogenannten Plattenkondensator, etwas näher untersuchen.
Ein Plattenkondensator besteht aus zwei parallelen Platten der Fläche A, die sich im Abstand s voneinander befinden, bei dem
sich auf jeder Platte die Ladung Q bzw. -Q befindet, und eine Spannung U zwischen den Platten liegt.
Plattenkondensator
Man kann das elektrische Feld im Plattenkondensator sowohl mit Hilfe der elektrischen Feldstärke als auch mit Hilfe der
elektrischen Flussdichte beschreiben.
Bei der Beschreibung des elektrischen Feldes durch die Feldstärke E wird von der Kraftwirkung des Feldes ausgegangen: da
F
U
ÅÅÅÅÅ
= E = ÅÅÅÅ
Å gilt:
Q
s
U
E = ÅÅÅÅ
ÅÅ
s
Elektrische Feldstärke E beim Plattenkondensator mit der Spannung U und einem
Plattenabstand s.
Bei der Beschreibung des elektrischen Feldes durch die ektrische Flussdichte D geht man von den Ladungen Q auf den
Plattenflächen A aus und erhält:
Q
D = ÅÅÅÅÅ
Å
A
Elektrische Flussdichte D beim Plattenkondensator mit einer Ladung Q (auf jeder
Platte) und einer Plattenfläche A.
Kapazität des Plattenkondensators
AD
eA
Für die Kapazität C des Plattenkondensators ergibt sich somit aus C = ÅÅÅÅ
Å = ÅÅÅÅ
ÅÅÅÅÅ = ÅÅÅÅ
ÅÅ Å :
U
Es
s
Q
e0 A
C0 = ÅÅÅÅ
ÅsÅÅÅÅÅ
mit Vakuum zwischen den Platten
Cs = er C0
mit einem Stoff zwischen den Platten
7
Elektrische Energie des Plattenkondensators
Die Arbeit zum Aufladen des Kondensators ist im elektrischen Feld als elektrische Feldenergie gespeichert, die beim
Entladen wieder freigesetzt wird. So kann zum Beispiel die Energie für eine Fotoblitzlampe einem aufgeladenen Kondensator
entnommen werden.
2
2
QU
Q
CU
Eel = ÅÅÅÅ
Å2ÅÅÅÅÅ = ÅÅÅÅ
ÅÅÅÅÅ = ÅÅÅÅÅÅÅÅ
ÅÅÅÅÅ
2C
2
Elektrische Feldenergie beim Plattenkonsator mit der Kapazität C und der Spannung U.
10.3 Magnetostatik: Strom, Magnetisches Feld
Elektrischer Strom I (bewegte Ladungen Q)
Der elektrische Strom I ist eine physikalische Grösse, die beschreibt wieviele Ladungsträger Q pro Zeiteinheit t einen bestimmten
Querschnitt passieren: I = ÅÅQÅtÅÅÅ bzw. Q = I t.
Der Strom hat das Formelzeichen I und wird in Ampere (A) gemessen. Das Ampere ist eine Basisgrösse des Internationalen
Einheitensystems (SI) und ist folgendermassen definiert.
Ein Ampere ist die Stärke eines elektrischen Stromes, der durch zwei geradlinige parallele Leiter mit einem Abstand von einem Meter
fliesst und der zwischen den Leitern je Meter Länge eine Kraft von 2 * 10-7 N hervorruft.
Aus der Beziehung Q = I t folgt auch die Umrechnung: 1 Ah = 3600 C.
Damit ein Strom überhaupt zustande kommt, muss eine Spannungsdifferenz (Potentialdifferenz) zwischen zwei Punkten
vorhanden sein. Wir werden dies später noch etwas Genauer untersuchen.
Ströme bzw. bewegte Ladungen können in vielen verschiedenen Situationen auftreten:
† Der in einem Leiter fliessende Strom besteht aus Elektronen, die sich aus dem Atomverband gelöst haben (Elektronengas)
und sich mit relativ kleiner Geschwindigkeit bewegen.
† Der in einem Elektrolyten fliessende Strom besteht aus positiv und negativ geladenen Ionen.
† Der in einem Teilchenbeschleuniger (Ultrahochvakuum) fliessende Strom besteht aus Elementarteilchen (z.B. Protonen).
† Der in einem Permanentmagneten fliessende Strom besteht aus atomaren Kreiströmen.
Ein Strom erzeugt ein magnetisches Feld
Wir haben im Abschnitt über die Elektrostatik gesehen, dass eine Ladung Q ein elektrisches Feld erzeugt, das durch die
elektrische Feldstärke E (oder elektrische Flussdichte D) und die dazugehörigen elektrischen Feldlinien beschrieben werden
kann.
Wir werden im Folgenden sehen, dass analog dazu ein Strom I ein magnetisches Feld erzeugt, das durch die magnetische
Feldstärke H (oder magnetische Flussdichte B) und die dazugehörigen magnetischen Feldlinien beschrieben werden kann.
Ein magnetisches Feld ist der Zustand des Raumes, in dem auf Magnete, ferromagnetische Stoffe, Ströme sowie bewegte
Ladungen Kräfte ausgeübt werden. Ein magnetisches Feld ist nur an seinen Wirkungen erkennbar und nachweisbar.
Durchflutungsgesetz
Um den Zusammenhang zwischen dem elektrischen Strom als Ursache des Feldes und der magnetischen Feldstärke zu
beschreiben, kann das Durchflutungsgesetz benutzt werden. Es lautet:
8
Durchflutungsgesetz: Das Integral der magnetischen Feldstärke längs einer geschlossenen Umlauflinie ist gleich der Summe der von
÷÷÷” ÷÷÷”
der Kurve eingeschlossenen Ströme, der sogenannten Durchflutung: ò H ds = ⁄ I
B ÷ ” ÷÷÷”
B ÷÷÷” ÷÷÷”
Analog zur Elektrostatik, wo ŸA E ds als elektrische Spannung bezeichnet wurde, nennt man ŸA H ds magnetische Spannung.
÷÷÷” ÷÷÷”
Der oben eingeführte Ausdruck ò H ds heisst magnetische Umlaufspannung (das Integral läuft entlang einer geschlossenen
Kurve).
Stromdurchflossener Leiter
Bei einem geraden Leiter ist die Feldstärke H entlang einer kreisförmigen (magnetischen) Feldlinie der Länge l = 2 p r im
Abstand r vom Leiter (aus Symmetriegründen) konstant und hat (auf Grund des Durchflutungsgesetzes
÷÷÷”
÷÷÷” ÷÷÷”
ò H ds = H ò ds = H 2 p r = I ) den Betrag:
H = ÅÅÅÅ
ÅIÅÅÅÅÅÅ
2pr
Magnetische Feldstärke H um einen stromdurchflossenen Leiter
A
Die magnetische Feldstärke H hat die Einheit: @HD = ÅÅÅÅÅ
m
Die magnetischen Feldlinien sind geschlossen. Im Gegensatz zu den elektrischen Feldlinien, die (in der Elektrostatik) in
positiven Ladungen starten und negativen Ladungen enden, gibt es keine magnetischen Ladungen (sogenannte magnetischen
Monopole) wo magnetische Feldlinien starten oder enden können. Die magnetischen Feldlinien sind immer geschlossen.
Die Richtung des magnetischen Feldes bei einem stromdurchflossenen Leiter ist durch die folgende Rechte Hand Regel
gegeben:
Wenn die rechte Hand den stromführenden Leiter umschliesst und der Daumen in Richtung des technischen Stroms (entgegengesetzt
zum Elektronenfluss) zeigt, dann geben die gekrümmten Finger die Richtung der Feldlinien an.
Zylinderspule
9
Wichtig für viele Anwendungen (Induktivitäten, Transformatoren, Generatoren, Elektromotoren) ist die Kenntnis der magnetischen Feldstärke innerhalb einer Zylinderspule. Für eine lange (lang heisst, dass die Länge l der Spule viel grösser ist als der
Radius einer Windung) Zylinderspule mit N Windungen durch die ein Strom I fliesst gilt:
H=N
ÅÅÅIlÅ
Magnetische Feldstärke H in einer langen Zylinderspule
Zylinderspule
Permanentmagnet
Permanentmagnet
Wir haben gesehen, dass durch Ströme magnetische Felder erzeugt werden können. Diese magnetischen Felder verschwinden,
wenn der Strom abgeschaltet wird.
Dies ist jedoch nicht der Fall bei den sogenannten Permanentmagneten, bei denen atomare Wirbelströme die magnetischen
Felder erzeugen.
Jeder Magnet hat zwei Pole, einen Nordpol und einen Südpol. Ein Pol kommt niemals allein vor. Die Pole zweier Magneten
üben eine Kraft aufeinander aus, wobei sich gleichartige Pole abstossen und ungleichartige Pole anziehen.
Die magnetischen Feldlinien sind in sich geschlossen und laufen ausserhalb des Magneten vom Nordpol zum Südpol und
innerhalb des Magneten in umgekehrter Richtung.
Magnetfeld der Erde
Die Erde hat auch ein Magnetfeld. Der magnetische Südpol der Erde liegt in der Nähe des geographischen Nordpols (47°
nördlicher Breite und 100° westlicher Länge). Der magnetische Nordpol liegt in der Nähe des geographischen Südpols (72°
südlicher Breite und 155° östlicher Länge). Eine frei bewegliche Magnetnadel stellt sich unter der Wirkung des magnetischen
Erdfeldes in Richtung der Feldlinien ein. Diese Richtung weicht sowohl von der Horizontalen (diese Abweichung wird mit
Inklination bezeichnet) als auch von der Nord-Süd-Richtung Abweichung wird mit Deklination bezeichnet) ab.
Ein magnetisches Feld übt eine Kraft auf eine bewegte Ladung und einen
stromdurchflossenen Leiter aus (Lorentzkraft)
Analog zur Elektrostatik wo ein elektrisches Feld (genauer: die Feldstärke E) eine Kraft F auf eine Ladung Q ausübt, übt auch
ein Magnetfeld (genauer: der magnetische Fluss B) eine Kraft F auf eine bewegte Ladung oder einen stromdurchflossenen
Leiter (dies sind auch bewegte Ladungen) aus (nicht jedoch auf eine ruhende Ladung!).
Kraft auf eine Punktladung (Lorentzkraft)
÷”
÷”
F = Q Iv” µ BM
F=Q v B
÷”
Kraft F auf eine mit der Geschwindigkeit v” bewegte Ladung Q
÷”
Betrag der Kraft F, falls v” ¦ B
10
In dieser Gleichung für die Kraft steht nicht die magnetischen Feldstärke, sondern die magnetische Flussdichte.
Analog zur Elektrostatik wo die elektrische Flussdichte D (berechnet aus der Ladungsdichte) die Ursache und die elektrische
Feldstärke E die Kraftwirkung (F = Q E) beschreibt, ist in der Magnetostatik die elektrische Feldstärke H (berechnet aus dem
Strom) die Ursache und die magnetische Flussdichte die Kraftwirkung (F = Q v B).
Im Vakuum sind H und B (analog zu E und D) über die (konstante) magnetische Feldkonstante m0 miteinander verknüpft. In
einer stofflichen Materie orientieren sich jedoch die magnetischen Dipole (Kreisströme) des Stoffs unter der Kraftwirkung des
Feldes in Feldrichtung. Bei gleich bleibender Feldstärke H ändert sich die magnetische Flussdichte B. Der Zusammenhang
wird durch die Permeabilitätszahl mr des Stoffs beschrieben. Diese Werte sind für verschiedene Materialien tabelliert.
Den Zusammenhang werden wir später noch etwas Genauer anschauen. Vorläufig müssen wir nur wissen, dass die magnetische Feldstärke H und die magnetische Flussdichte B in folgendem Zusammenhang stehen.
B = m0 H
Magnetische Flussdichte im Vakuum
B = m H = mr m0 H
Magnetische Flussdichte in einem Körper mit der Permeabilitätszahl mr
m = mr m0
Permeabilität
B
mr = ÅÅÅÅÅÅÅÅ
ÅÅÅÅÅÅÅÅ
ÅÅÅÅ
B
Permeabilitätszahl des Stoffs ( Ø Tabelle)
Vakuum
m0 =
Vs
4 p * 10-7 ÅÅÅÅ
ÅÅÅÅÅÅ
Am
magnetische Feldkonstante
Vs
Die magnetische Flussdichte hat die SI Einheit: @BD = ÅÅÅÅ
ÅÅÅÅ = Tesla HTL
m2
Die Permeabilitätszahl mr gibt an, wie sich die magnetische Flussdichte ändert, wenn sich am entsprechenden Ort statt eines Vakuums
oder Luft ein Stoff befindet.
Kraft auf einen stromdurchflossenen Leiter
Jeder Strom in einem Leiter besteht aus bewegten Ladungen, auf die ebenfalls die Lorentzkraft wirkt.
” ÷”
÷”
F = I Il µ BM
F=I l B
F = I l B sinHaL
Kraft auf einen stromführenden Leiter der Länge l im Magnetfeld
÷”
Betrag der Kraft, falls v” ¦ B
Kraft eines Magnetfeldes B auf einen stromdurchflossenen Leiter, wobei a den Winkel
zwischen dem Magnetfeld und dem Leiter angibt.
Das Symbl µ steht in obiger Gleichung für das Vektorprodukt.
Die Richtung der Kraft ist durch die "Rechte Hand Regel für die Kraft auf einen stromdurchflossenen Leiter im Magnetfeld"
gegeben.
Wenn der Daumen in Richtung des Stromes im stromführenden Leiter und der Zeigefinger in Richtung des magnetischen Feldes
zeigen, dann zeigt der Mittelfinger in Richtung der auf den Leiter wirkenden Kraft.
11
÷”
” ÷”
Anwendungen der Beziehung F = Q Iv ¥ BM
† Kreisbahn: Zyklotron, Synchrotron
† Hall Effekt
Zwei Ströme üben Kräfte aufeinander aus
Ein stromdurchflossener Leiter erzeugt ein Magnetfeld. Dieses Magnetfeld übt eine Kraft auf einen zweiten stromdurchflossenen Leiter aus. Das Gleiche kann für den zweiten Leiter gesagt werden.
Zusammengefasst: Zwei Ströme üben Kräfte aufeinander aus.
Insbesondere gilt für zwei parallele stromdurchflossene Leiter. Sie ziehen sich an, wenn die Ströme in die gleiche Richtung
gehen, andernfalls stossen sie sich ab. Die Grösse der Kraft ist gegeben durch:
m I1 I2
F = ÅÅÅÅÅÅÅÅ
ÅÅÅÅÅÅÅÅ
2pr
Kraft zwischen zwei parallelen stromdurchflossenen Leitern im Abstand r
Auf dieser Beziehung beruht die gesetzliche Definition der Stromstärkeeinheit Ampere als SI Basiseinheit.
Ein Ampere ist die Stärke eines elektrischen Stromes, der durch zwei geradlinige parallele Leiter mit einem Abstand von einem Meter
fliesst und der zwischen den Leitern je Meter Länge eine Kraft von 2 * 10-7 N hervorruft.
Permeabilität
Wir haben gesehen, dass der Zusammenhang zwischen der magnetischen Feldstärke H und der magnetischen Flussdichte B
durch die Gleichung B = m H gegeben ist.
Die Permeabilität m = mr m0 beschreibt das magnetische Verhalten des Stoffs.
Es können verschiedene magnetische Verhaltensweisen unterschieden werden. Die wichtigsten Typen sind: Diamagnetismus,
Paramagnetismus und Ferromagnetismus.
12
Diamagnetismus mit mr < 1: diese Stoffe schwächen das Feld geringfügig.
Beispiele: Silber, Kupfer, Bismut.
Paramagnetismus mit 1 < mr : diese Stoffe stärken die magnetische Flussdichte geringfügig.
Beispiele: Platin, Aluminium, Luft.
Ferromagnetismus mit 1 << mr : diese Stoffe stärken die magnetische Flussdichte sehr stark.
Beispiele: Eisen, Cobalt, Nickel.
Bei ferromagnetischen Materialien ist m nicht eine Konstante und es kann nicht die einfache Beziehung B = m H verwendet
werden. Die magnetische Flussdichte hängt in komplizierter Weise von der angelegten magnetischen Feldstärke und der
Vorgeschichte ab wie die untenstehende Magnetisierungskurve zeigt:
Beim erstmaligen Magnetisieren (Anlegen eines Feldes H) folgt die magnetische Flussdichte B der sogenannten Neukurve bis
sie bei der Sättifungsfeldstärke die maximale Sättigungsflussdichte erreicht. Bei weiterer Erhöhung der Feldstärke nimmt die
Flussdichte nicht mehr zu. Beim Ummagnetisieren verläuft die Flussdichte dann entlang des oberen Astes. Bei einer Feldstärke 0 geht die Flussdichte nicht auf 0 zurück, sondern es bleibt die sogenannte Remanenzflussdichte BR . Die Feldstärke
muss bis zur Koerzitivstärke HK in die andere Richtung umgepolt werden bis die Flussdichte auf 0 zurückgeht. Beim einem
vollen Ummagnetisierungszyklus werden nacheinander beide Äste der Magnetisierungskurve durchlaufen, die eine sog.
Hysteresisschleife bilden.
10.4 Elektrodynamik: Induktion
In der Elektrostatik haben wir uns mit zeitlich konstanten Ladungsverteilungen und deren Wechselwirkungen und in der
Magnetostatik mit zeitlich konstanten Strömen und deren Wechselwirkungen beschäftigt.
In diesem Abschnitt sollen nun auch zeitlich veränderliche Situationen (z.B. Bewegung eines Leiters, Einschalten eines
Stromes) untersucht werden.
Dabei treffen wir auf ein neues Phänomen: die Induktion einer Spannung in einem Leiter.
Eine Spannung lässt sich auf zwei Arten in einem Leiter induzieren: durch Bewegen des Leiters in einem Magnetfeld oder
durch Ändern des magnetischen Flusses durch den Leiter.
13
Induktion durch Bewegen eines Leiters im Magnetfeld
Wenn ein Leiter senkrecht zu den Feldlinien durch ein Magnetfeld bewegt wird, so wirkt die Lorentzkraft entlang des
Drahtes. Die Lorenztkraft pumpt also Elektronen auf die eine Seite, so dass das eine Drahtende negativ und das andere Ende
positiv geladen wird. Dadurch entsteht im Leiter ein Feld und zwischen den Enden des Leiters eine elektrische Spannung, die
man Induktionsspannung nennt.
Die Grösse der Induktionsspannung ergibt sich aus der Überlegung, dass im Gleichgewicht die Loretzkraft FL und die elektrische Kraft FE auf Grund der induzierten Spannung den gleichen Betrag haben müssen: FL = e v B = FE = e E. Daraus folgt
für die Spannung
Uind = l E = l v B
wenn l die Länge des Leiters darstellt.
”
Wenn die Richtung l entlang des Leiters und die Bewegung v” des Leiters nicht aufeinander senkrecht stehen gilt
” ÷ ” ” ” ÷”
Uind = l E = l Iv µ BM; das heisst, dass die Winkel zwischen den verschiedenen Grössen berücksichtigt werden müssen. In
dieser Gleichung kommt sowohl das Skalarprodukt als auch das Vektorprodukt vor.
Induktion durch Änderung des magnetischen Flusses
Eine Induktion ist jedoch auch möglich, wenn sich der Leiter nicht bewegt (also keine Loretzkraft wirken kann).
Wenn sich eine Leiterschleife im Magnetfeld einer Spule befindet und sich durch Änderung des Spulenstroms die Stärke des
Magnetfelds ändert, wird auch eine Spannung induziert. Diese Spannung ist umso grösser je schneller das Magnetfeld
geändert wird.
Mit Hilfe des magnetischen Flusses f lässt sich die induzierte Spannung quantitativ angeben.
÷”
÷” ÷÷÷÷÷”
Die physikalische Grösse magnetischer Fluss f ist das Integral der magnetischen Flussdichte B über die Fläche A: f = Ÿ B dA. Dies
führt auf f = B A, falls das Magnetfeld senkrecht auf der Fläche steht.
÷÷÷÷÷”
Die Richtung einer (ebenen) Fläche bzw. eines infinitesimalen Flächenelements dA ist durch die Flächennormale gegeben.
Mit Hilfe des magnetischen Flusses lässt sich das Induktionsgesetz folgendermassen formulieren:
df
Induktionsgesetz: Die zeitliche Änderung des magnetischen Flusses ÅÅÅÅ
ÅÅÅ durch eine Fläche A, die von einem Leiter umgeben ist,
dt
df
induziert in diesem Leiter eine Spannung Uind mit: Uind = - ÅÅÅÅdtÅÅÅ
14
df
Das Minuszeichen in Uind = - ÅÅÅÅ
ÅÅ bedeutet, dass Induktionsspannung und Induktionsstrom der sie erzeugenden Flussänderung
dt
entgegenwirken (Lenz'sche Regel). Bei einer Zunahme des magnetischen Flusses fliesst der induzierte Strom also entgegengesetzt zu der sich aus der Korkenzieherregel ergebenden Richtung.
Die zeitliche Veränderung des magnetischen Flusses kann durch Veränderung der Grösse des Magnetfelds oder durch Drehen
÷÷÷÷÷”
÷”
der Leiterschleife (B und dA ändern ihre Richtung zueinander) im fixen Magnetfeld erreicht werden.
Selbstinduktion
Nach dem Induktionsgesetz treten Induktionsspannungen dann auf, wenn sich der magnetische Fluss durch eine Leiterschleife
verändert. Dabei spielt es keine Rolle, ob dieser Fluss durch ein von aussen angelegtes Feld order durch das Feld des Stroms
im eigenen Leiterkreis zustande kommt.
Jede Änderung eines Stroms in einem Leiterkreis oder in einer Spule ändert das Feld und damit den Fluss durch den eigenen
Leiterkreis. Dies hat Indunktionswirkungen zur Folge, die man als Selbstinduktion bezeichnet.
Da das Magnetfeld eines Stromkreises an jeder Stelle proportional zum Strom ist, lässt sich der Fluss f des eigenen Feldes
schreiben als f = L I. Der Proportionalitätsfaktor wird Induktivität (oder Selbstinduktionskoeffizient) genannt. Er hängt von
der Geometrie des Leiterkreises und vom Spulenkern ab.
Für eine lange Spule gilt: f = N B A = N m H A = m N 2 ÅÅÅÅAl Å I
Daraus folgt mit f = L I für die Induktivität: L = m N 2 ÅÅÅÅAl Å
2
Tm
Vs
Die Einheit der Induktivität ist: @LD = ÅÅÅÅÅÅÅÅ
ÅÅÅÅ = ÅÅÅÅ
ÅÅ Å = Henry HHL
A
A
Spulen sind Energiespeicher. Eine stromdurchflossene Spule speichert in ihrem Feld bei einem Strom I eine magnetische Energie von:
Wm = ÅÅÅÅ12 L I 2 .
Anwendungen
† Transformator
† Generator
† Wirbelstrombremse
10.5 Stromkreise
Einleitung
In diesem Abschnitt untersuchen wir Stromkreise. Man unterscheidet grundsätzlich zwischen Gleichstromkreisen und Wechselstromkreisen.
Bei Gleichstromkreisen ist die Stromstärke konstant.
Bei Wechselstromkreisen ist die Stromstärke zeitabhängig. Beispielsweise sind bei Einschalt- und Ausschaltvorgängen die
Spannungen und Ströme zeitabhängig. Weiters spielen die (zeitabhängigen) sinusförmigen Spannungen und Ströme eine
wichtige Rolle.
Wir untersuchen im Folgenden aus Zeitgründen jedoch nur Gleichstromkreise. Ausserdem enthalten die untersuchten Stromkreise nur Spannungsquellen und Ohmsche Widerstände.
15
Begriffe und Komponenten
Spannungsquelle
Zwischen den Polen einer Spannungsquelle herrscht die Quellenspannung. Sie ist die Ursache des elektrischen Stroms. Am
Minuspol besteht ein Elektronenüberschuss, am Pluspol ein Elektronenmangel. Beide Zustände werden durch Vorgänge im
Inneren der Spannungsquelle erzeugt und aufrechterhalten. Die Elektronen fliessen ausserhalb der Spannungsquelle vom
Elektronenüberschuss zum Elektronenmangel, also vom Minuspol zum Pluspol. Vor Kenntnis der wahren Verhältnisse war
bereits festgelegt worden.
Technische Stromrichtung: Der Strom fliesst vom Pluspol zum Minuspol.
Skizze zur Spannungsquelle:
In einem Stromkreis muss zwischen folgenden Spannungen unterschieden werden:
† Die Quellenspannung UQ (oder Urspannung oder Elektromotorische Kraft EMK) ist die Spannung zwischen den Polen
einer Spannungsquelle bei nicht geschlossenem Stromkreis (Leerlauf-Spannung).
† Der Innere Spannungsabfall Ui ist der Spannungsabfall am inneren Widerstand (Innenwiderstand Ri ).
† Die Klemmenspannung UK ist die Spannung zwischen den Polen einer Spannungsquelle bei geschlossenem Stromkreis.
Nur diese Spannung steht für den äusseren Stromkreis zur Verfügung. Sie entspricht dem gesamten äusseren Spannungsabfall. Sie ist gleich der Summe der äusseren Spannungsabfälle.
Es gilt somit:
UQ = UK + Ui
Ø
und
U
Q
I = ÅÅÅÅÅÅÅÅ
ÅÅÅÅ
ÅÅÅÅ .
R +R
i
a
Ri
Ra
Q
UK = UQ - Ui = UQ - I Ri = UQ - ÅÅÅÅÅÅÅÅ
ÅÅÅÅ
ÅÅÅÅ Ri = I1 - ÅÅÅÅÅÅÅÅ
ÅÅÅÅÅÅÅÅ M UQ = ÅÅÅÅÅÅÅÅ
ÅÅÅÅÅÅÅÅ UQ
R +R
R +R
R +R
U
i
a
i
a
i
a
Spannung, Spannungsabfall
Die Spannung U zwischen zwei Punkten eines Leiters ist das Verhältnis der in diesem Leiterteil umgesetzten Leistung W zu dem
durch den Leiter fliessenden Strom I: d.h. U = ÅÅÅÅPI Å .
W
Dies können wir einfach herleiten, indem wir die weiter vorne eingeführte Definition für die Spannung U = fA,B = ÅÅÅÅ
ÅÅ
Q
Wêt
W
P
verwenden und schreiben: U = ÅÅÅÅQÅÅ = ÅÅÅÅQêt
ÅÅÅÅÅ = ÅÅÅÅI Å .
W
Die Einheit der Spannung ist: @UD = ÅÅÅÅ
ÅÅ = Volt HV L
A
Das Volt ist die elektrische Spannung zwischen zwei Punkten eines metallischen Leiters, in dem bei einem konstanten Strom von 1 A
zwischen den beiden Punkten eine Leistung von 1 W umgesetzt wird.
16
Der Spannungsabfall ist die Spannung zwischen zwei beliebigen Punkten eines stromdurchflossenen Leiters.
Der Spannungsabfall ist stets kleiner als die Quellenspannung.
Elektrischer Widerstand (Ohm)
U
Der Widerstand R ist das Verhältnis der Spannung U zwischen den Enden eines Leiters zur Stärke des Stroms I im Leiter: d.h. R = ÅÅÅÅ
ÅÅ .
I
V
Die Einheit des Widerstands R ist: @RD = ÅÅÅÅÅ
Å = Ohm HWL.
A
Das Ohm ist der elektrische Widerstand zwischen zwei Punkten eines metallischen Leiters, durch den bei der Spannung 1 V zwischen
den beiden Punkten ein Strom von 1 A fliesst.
Den Kehrwert des Widerstands R bezeichnet man als elektrischen Leitwert G: d.h. G = ÅÅÅÅR1Å .
Die Einheit des elektrischen Leitwerts G ist: @GD = ÅÅW1ÅÅÅÅ = Siemens HSL
Der Widerstand ist bei einem sogenannten ohmschen Widerstand konstant. Die Strom-Spanungs Kennlinie (I als Funktion
von U) ist in diesem Fall eine Gerade mit der Steigung G.
† ohmsches Gesetz: U = R I bzw. I = ÅÅÅÅR1Å U = G U
Im allgemeinen ist jedoch der Widerstand R spannungsabhängig. Da bei höherer Spannung mehr Energie in Wärme umgewandelt wird, steigt die Temperatur.
† Bei Leitern steigt dann der Widerstand auf Grund der vermehrten Stösse der Elektronen an den durch die Erwärmung
schnelleren Bewegungen der Gitteratome.
† Bei Halbleitern fällt dann der Widerstand, da mehr Ladungsträger zur Verfügung stehen.
Der Widerstand eines Leiters ist proportional zur Länge l des Leiters und umgekehrt proportional zur Querschnittsfläche A des Leiters.
rl
Die Proportionalitätskonstante ist der sogenannte materialabhängige spezifische Widerstand r (siehe Tabellen): R = ÅÅÅÅ
ÅÅÅ
A
Der spezifische Widerstand ist temperaturabhängig und wird üblicherweise für eine Temperatur von 20 °C tabelliert (r20 ).
Die Widerstandsänderung für eine andere Temperatur kann (in erster, linearer Näherung) mit Hilfe des Temperaturkoeffizienten des elektrischen Widerstands a (auch für 20 °C tabelliert) berechnet werden:
rHTL = r20 H 1 + aHT - 20 °CL L
Bei einigen Metallen sinkt der Widerstand in der Nähe des absoluten Nullpunkts sprunghaft annähernd auf R = 0. Dies wird
mit Supraleitung bezeichnet.
Die elektrische Leitfähigkeit ¿ ist der Kehrwert des spezifischen Widerstands r: d.h. ¿ = ÅÅÅÅ1rÅ .
Gleichstromkreise
Stromkreis
In einem Stromkreis fliessen die Elektronen ausserhalb der Spannungsquelle vom Minuspol zum Pluspol und innerhalb der
Spannungsquelle vom Plus zum Minuspol wieder zurück.
Bei der Analyse von Stromkreisen sind die folgenden zwei Kirchhoffschen Gesetze von grosser Bedeutung.
17
Knotenpunktsatz (1. Kirchhoffsches Gesetz)
In jedem Verzweigungspunkt (Knotenpunkt) eines Stromkreises ist die Summe der zufliessenden Ströme gleich der Summe der
abfliessenden Ströme.
Insbesondere gilt auch:
In einem unverzweigten elektrischen Stromkreis ist an allen Stellen die Stromstärke gleich gross.
Skizze zum Knotenpunktsatz:
Maschensatz (2. Kirchhoffsches Gesetz)
In einem unverzweigten Stromkreis bzw. in jeder Masche (geschlossener Pfad) eines verzweigeten Netzwerks ist die Summe (mit
Vorzeichen) aller Quellenspannungen gleich der Summe aller inneren und äusseren Spannungsabfälle.
Skizze zum Maschensatz:
Reihenschaltung
Bei einer Reihen- oder Serienschaltung sind die Widerstände hintereinandergeschaltet, d.h. jeder von ihnen wird nacheinander
vom gleichen Strom I durchflossen.
Bei einer Reihenschaltung von Widerständen ist der Gesamtwiderstand gleich der Summe der Einzelwiderstände:
RR = R1 + R2 + R3 + ...
U1 +U2 +U3 +...
U1
U2
U3
U
denn: RR = ÅÅÅÅ
Å = ÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅ
ÅÅÅÅÅÅÅÅÅÅÅÅÅÅ ÅÅ = ÅÅÅÅ
ÅÅÅÅ + ÅÅÅÅ
ÅÅÅÅ + ÅÅÅÅ
ÅÅÅ + ... = R1 + R2 + R3 + ...
I
I
I
I
I
Skizze zur Reihenschaltung:
Parallelschaltung
Bei einer Parallelschaltung sind die Widerstände parallel zueinander geschaltet, d.h. an jedem erfolgt der gleiche Spannungsabfall U.
18
Bei einer Parallelschaltung von Widerständen ist der Kehrwert des Gesamtwiderstands RP gleich der Summe der Kehrwerte der
1
1
1
1
Einzelwiderstände: ÅÅÅÅ
ÅÅÅ = ÅÅÅÅ
ÅÅÅÅ + ÅÅÅÅ
ÅÅÅ + ÅÅÅÅ
ÅÅÅÅ + ... oder GP = G1 + G2 + G3 + ...
R
R
R
R
P
1
2
3
I1 +I2 +I3 +...
I1
I2
I3
1
I
1
1
1
denn: ÅÅÅÅ
ÅÅÅÅ = ÅÅÅÅ
Å = ÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅ
ÅÅÅÅÅÅÅÅÅÅÅÅ = ÅÅÅÅ
Å + ÅÅÅÅ
Å + ÅÅÅÅ
Å + ... = ÅÅÅÅ
ÅÅ + ÅÅÅÅ
ÅÅ + ÅÅÅÅ
ÅÅ + ...
RP
U
U
U
U
U
R1
R2
R3
Bei einer Parallelschaltung ist der Gesamtwiderstand kleiner als der kleinste Einzelwiderstand.
Skizze zur Parallelschaltung:
Elektrische Arbeit
Elektrische Energie entsteht aus anderen Energiearten und lässt sich wieder in andere umwandeln. Auch für sie gilt der Satz
von der Erhaltung der Energie.
Unter der Kraftwirkung eines elektrischen Feldes bewegen sich Ladungsträger Q durch den Leiter. Damit die Ladung Q einen
Spannungsabfall U überwinden kann, muss die Arbeit Q U geleistet werden. Mit Q = I t sowie U = R I folgt für die Arbeit W :
2
U t
Arbeit W = U I t = ÅÅÅÅ
ÅÅÅÅÅÅ = I 2 R t
R
Diese Beziehung gilt für ohmsche Widerstände und für den Fall, dass die Stromstärke I während der Zeit t konstant ist. Dann
bewegen sich die Ladungsträger mit konstanter Geschwindigkeit, die gesamte elektrische Arbeit wird in Wärme umgewandelt.
Aus obiger Beziehung folgt für die Leistung P (bzw. die pro Zeiteinheit in Wärme umgewandelte elektrische Energie) bei
einem ohmschen Widerstand:
2
W
U
Leistung P = ÅÅÅÅ
ÅÅ = U I = ÅÅÅÅ
ÅÅÅÅÅ = I 2 R
t
R