Lösungen

Grundlagen der Physik 2
Lösung zu Übungsblatt 5
Daniel Weiss
3. Mai 2010
Inhaltsverzeichnis
Aufgabe 1 - Kugelkondensator
1
Aufgabe 2 - Elektrostatisches Feld
3
a) Skizze des Kondensators . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
b) Potential und elektrisches Feld . . . . . . . . . . . . . . . . . . . . . . . . . .
c) Skizze des Potentials und des Feldes . . . . . . . . . . . . . . . . . . . . . . .
a) Rotation . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
b) Divergenz . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
c) Potential . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Aufgabe 3 - Ladungsdreieck
a) Potential und pot. Energie bei T
b) Energie nach Auslenkung um h
c) parabolisches Potential . . . . .
d) Schwingungsfrequenz . . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
1
1
2
3
3
3
4
4
4
4
4
Aufgabe 4 - Magnetfeld und Magnetische Induktion
4
Aufgabe 5 - Zwei Kreisförmige Leiter
5
Aufgabe 6 - Solenoid
5
Aufgabe 1
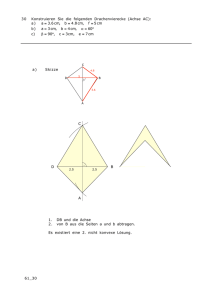
a) Skizze:
b) Mit dem Satz von Gauÿ können die Potentiale in den drei Bereichen I,II und III
berechnet werden. Dabei haben einschlieÿende Kugelschalen keinerlei Einuss auf
1
Q1
III
r2
II
I
Q2
r1
Abbildung 1: Skizze des Kondensators
das Feld in ihrem Inneren.
Z
~ =
~ dA
E
Z
∂V
V
ρ
dV
0
(1)
⇒ E1 = 0
1 Q2
4π0 r2
1 Q1 + Q2
⇒ E3 =
4π0
r2
⇒ E2 =
∀r < r2
(2)
∀r2 < r < r1
(3)
∀r1 < r
(4)
Das Potential ist
Z
Φ=−
(5)
~
~ dr
E
⇒ Φ1 = const.
1 Q2
⇒ Φ2 =
4π0 r
1 Q1 + Q2
⇒ Φ3 =
4π0
r
∀r < r2
(6)
∀r2 < r < r1
(7)
∀r1 < r
(8)
c) Bei den unendlich dünnen Platten macht das elektrische Feld einen Sprung. Hierbei
wurde auf der inneren Schale eine negative Ladung und auf der äuÿeren eine positive
Ladung angenommen.
Dieselbe Ladungsanordnung führt zu folgendem Potential:
2
Abbildung 2: qualitative Skizze des elektrischen Feldes
Abbildung 3: qualitative Skizze des elektrischen Potentials
Aufgabe 2
a)


0
~ =∇
~ ×E
~ =  0  = ~0
rot E
6x − 6x
(9)
Es kann sich also um ein elektrostatisches Feld handeln!
b)
~ =∇
~E
~ = 6y − 6y + 0 = 0 ⇒ ρ = 0
div E
3
(10)
c)
Z
Ex dx = −3x2 y + C(y, z)
(11)
Z
Ey dy = −3x2 y + y 3 + C(x, z)
(12)
Ez dz = −C(x, y)
(13)
⇒ Φ(x, y, z) = y 3 − 3x2 y
(14)
−
−
Z
−
Aufgabe 3
a) Alle drei Vektoren von den einzelnen Ladungen Q zu T sind vom Betrag her gleich.
Also genügt es Einen zu berechnen.
a
2r
√
a2
a 3
1
2
a −
=
ry =
3
4
6
r
2
2
a
a
a
+
=√
⇒ k~rk2 =
4
12
3
√
1 3 3Q
⇒Φ=
4π0 a
√
1 3 3QT
⇒ Epot =
4π0
a
rx =
(15)
(16)
(17)
(18)
(19)
b) Für eine anziehende Wirkung muss sgn(T ) = − sgn(Q) gelten. Die potentielle Energie ändert sich zu
1
3QT
q
Epot =
(20)
4π0
1 2
3a
+ h2
c)
d)
Aufgabe 4
Mit dem Satz von Stokes folgt aus den Maxwell-Gleichungen das Ampèresche Gesetz:
I
∂A
~ =
~ ds
H
Z
~ =
~ dA
rot H
A
~
~ =I
~j + ∂ D dA
∂t
A
|{z}
Z
=0
4
(21)
In Polarkoordinaten folgt:
I
~ =
~ ds
H
Z
∂A
und daraus die Induktion:
2π
Hr dr ⇒ H =
0
I
= 15,92H
2πr
(22)
(23)
B = µ0 H = 1,26 · 10−6 T
Aufgabe 5
Das Biot-Savartsche Gesetz für den Fall einer Leiterschleife mit Beobachtungsort auf einer
Geraden, die senkrecht zu jedem Tangentialvektor steht und durch den Mittelpunkt geht
lautet:
µ0 IπR2
(24)
Bx =
3
2π(x2 + R2 ) 2
Das gesamte Magnetfeld ist die Summe der beiden einzelnen Felder:
H=
I1 πr12
3
2π(x21 + r12 ) 2
+
I2 πr22
3
2π(x22 + r22 ) 2
= 16,76H
(25)
Aufgabe 6
Formel für die Gegenindultion L:
L = µ0
N1 N2 A
= 25,13µH
l
5
(26)