61_23 Konstruieren Sie die folgenden Dreiecke: a - SOS

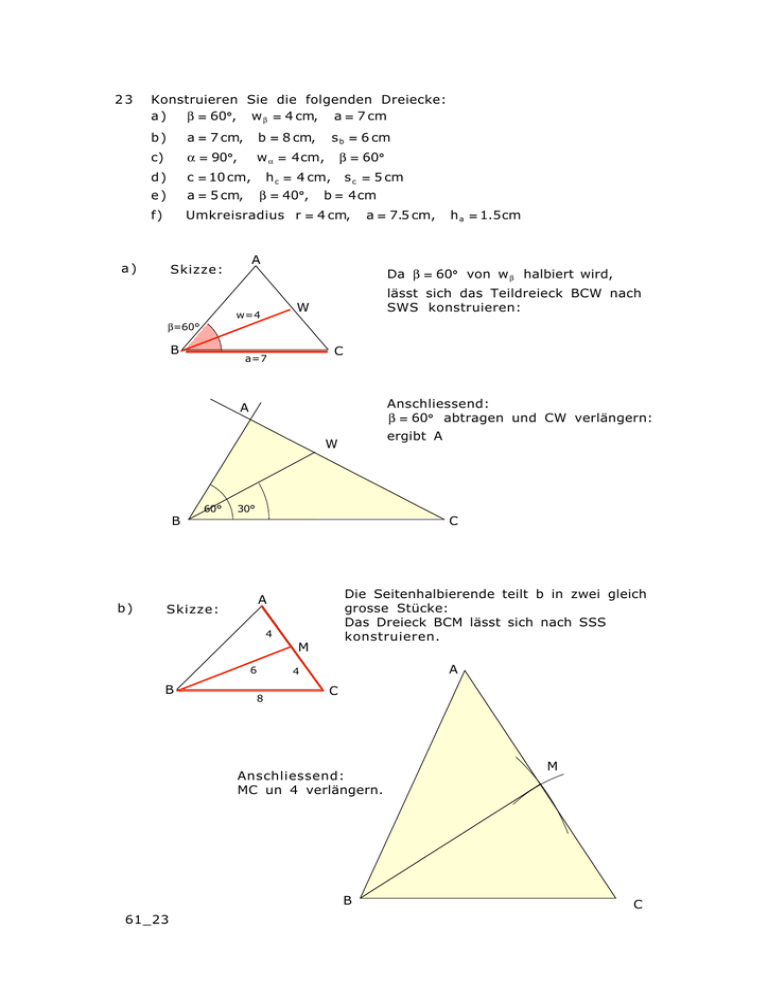
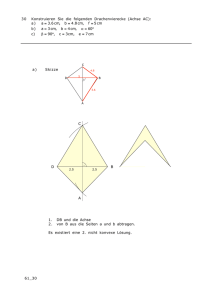
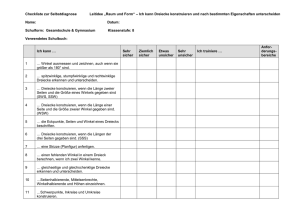
23
Konstruieren Sie die folgenden Dreiecke:
a)
= 60°, w = 4 cm, a = 7 cm
b)
a = 7 cm,
b = 8 cm,
s b = 6 cm
c)
= 90°,
w = 4cm,
= 60°
d)
e)
c = 10 cm, h c = 4 cm, s c = 5 cm
a = 5 cm, = 40°, b = 4cm
f)
Umkreisradius r = 4 cm,
a)
a = 7.5 cm,
A
Skizze:
h a = 1.5cm
Da = 60° von w halbiert wird,
lässt sich das Teildreieck BCW nach
SWS konstruieren:
W
w=4
=60°
B
C
a=7
Anschliessend:
= 60° abtragen und CW verlängern:
ergibt A
A
W
B
b)
60°
30°
C
Die Seitenhalbierende teilt b in zwei gleich
grosse Stücke:
Das Dreieck BCM lässt sich nach SSS
konstruieren.
A
Skizze:
4
M
6
B
8
A
4
C
Anschliessend:
MC un 4 verlängern.
B
61_23
M
C
c)
B
Skizze:
60°
W
Wir beginnen mit dem rechten Winkel
und der Winkelhalbierenden;
4
90°
C
A
B
Irgendwo an c einen 60°-Winkel zeichnen,
a‘ parallel verschieben, bis sie durch W geht.
W
60°
c
a‘
90°
C
d)
Skizze:
Das rechtwinklige Dreieck HMC ist einfach
zu konstruieren; beginnen sie mit dem
rechten Winkel.
C
5
4
A
A
H
B
M
5
5
C
A
H
M
Messen Sie dann von M aus je 5cm nach links und rechts ab.
B
e)
Skizze:
4
A2
B
40°
C
5
Beginnen Sie mit der seite BC und
dem Winkel .
Die Seite CA lässt sich auf zwei
verschiedene Arten abtragen:
2 Lösungen möglich!
f)
A1
B
C
Skizze:
Beginnen sie mit dem Kreis und tragen
Sie darin eine Sehne der Länge 7.5 ab.
A
r=4
1.5
B
7.5
C
h a bedeutet, dass der Abstand des Punktes a von
der Seite a 1.5cm ist.
Auf beiden seiten von a ist ein Streifen der Breite
1.5 zu zeichnen.
Aus den 4 möglichen Punkten für A ergeben sich 2
verschiedene Dreiecke.
C
A1
B
A2