Übungsaufgaben Rep. Geometrie, Dreieckskonstruktionen RepG/DR

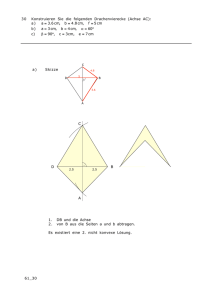
Übungsaufgaben Rep. Geometrie, Dreieckskonstruktionen
Mathematik
T. Hunziker, dipl. math., dipl. ML
RepG/DR
www.hunziker.jimdo.com
Okt 13
Hilfsmittel: Taschenrechner, Formelblatt GBMS, Geodreieck, Lineal, Zirkel.
Jede Aufgabe gibt 2 Punkte. Bei Dreieckskonstruktionen gibt es für jede
Zusatzlösung einen Punkt.
Aufgabe 1
Rechteck
Rhombus
gleichseitiges
Dreieck
Reguläres
Sechseck
a) Welche der vier Figuren sind
punktsymmetrisch?
b) Zeichnen Sie alle SymmetrieAchsen ein, mit Lineal!
Aufgabe 2
Berechnen Sie den Flächeninhalt A eines
gleichschenkligen Dreiecks mit
Schenkellänge 17 cm und Basislänge 16 cm.
Aufgabe 3
Konstruieren Sie auf separatem Blatt ein Dreieck mit den Seitenlängen 12 cm, 11 cm und 8 cm.
Konstruieren Sie dann a) den Umkreis, b) den Inkreis, c) den Höhenschnittpunkt H und d) den
Schwerpunkt S des Dreiecks!
Aufgabe 4
Konstruieren Sie eine Figur, die punktsymmetrisch, aber nicht achsensymmetrisch ist.
Aufgabe 5
Zu a) bis e): Konstruieren Sie mit den vorgegebenen Angaben jeweils ein Dreieck. Es sind immer alle
möglichen Lösungen zu konstruieren. Ausnahme: kongruente Lösungen. Jede Aufgabe gibt zwei
Punkte, für jede Zusatzlösung gibt es einen Zusatzpunkt.
Zu jeder Konstruktion ist ein kurzer Konstruktionsbericht (KB) verlangt!
a) Seite a = 3.6 cm, Seite c = 3.5 cm, Höhe h a = 3.2
b) Winkel γ = 90°, Höhe hc = 3 cm, Höhe ha = 3.9 cm
c) Seite c = 7 cm, Seitenhalbierende sa = 4.8 cm, Seitenhalbierende sc = 3.6 cm
d) Seite a = 6 cm, Höhe hb = 5.6 cm, Seitenhalbierende sc = 4 cm
e) Seite a = 4.9 cm, Höhe hb = 4.2 cm, Höhe ha = 7.2 cm
Lösungen zu Übungsaufgaben Rep. Geometrie, Dreieckskonstruktionen
Aufgabe 1
Rechteck
Rhombus
gleichseitiges
Dreieck
Reguläres
Sechseck
a) Welche der vier Figuren sind
punktsymmetrisch?
Rechteck, Rhombus, Reg. Sechseck
b) Zeichnen Sie alle SymmetrieAchsen ein, mit Lineal
Aufgabe 2
Berechnen Sie den Flächeninhalt eines
gleichschenkligen Dreiecks mit
Schenkellänge 17 cm und Basislänge 16 cm.
2
2
h= 17 −8 = 15 cm
17
8
h
A =
gh
16⋅15
2
=
= 120 cm
2
2
Aufgabe 3
Konstruieren Sie auf separatem Blatt ein Dreieck
mit den Seitenlängen 12 cm, 11 cm und 8 cm.
Konstruieren Sie dann a) den Umkreis,
b) den Inkreis, c) den Höhenschnittpunkt H und
d) den Schwerpunkt S des Dreiecks!
Lösung:
H
S
I
U
Aufgabe 4
Konstruieren Sie eine Figur, die punktsymmetrisch, aber nicht achsensymmetrisch ist.
Lösung: Zum Beispiel ein Parallelogramm
Aufgabe 5
Die Lösungen zu den Dreieckskonstruktionen können im Unterricht oder im Internet eingesehen
werden.
Lösungen zu Übungsaufgaben Rep. Geometrie, Dreieckskonstruktionen
(Fortsetzung)
Lösung zu Aufgabe 5a)gabe 1
Seite a = 3.6 cm, Seite c = 3.5 cm, Höhe ha = 3.2
Skizze:
Konstruktion:
C
C
3.2
3.6
3.2
A
B
3.5
B
A1
KB:
- Höhenstreifen 3.2 cm
- C wählen, c = 6 cm -> B
- Von B aus 6 cm abtragen -> A
- (2 Lösungen)
A2
Lösung zu Aufgabe 5b)gabe 1
Winkel γ = 90°, Höhe hc = 3 cm, Höhe ha = 3.9 cm
Skizze:
C
KB:
3.9
3
B
A
Konstruktion:
C
90°
- Höhenstreifen 3 cm
- C wählen
- k(C, 3.9 cm) -> A
- 90° bei C abtragen -> B
Höhe h a= Seite b
(w eil das Dreieck
rechtw inklig ist)
A
B
Lösung zu Aufgabe 5c)gabe 1
Seite c = 7 cm, Seitenhalbierende sa = 4.8 cm, Seitenhalbierende sc = 3.6 cm
Skizze:
C
Konstruktion:
C
3.6
4.8
A
S
Mc
7
Ma
S
B
KB:
- AB = 7 cm, Mc in der Mitte von AB
- 1/3 von 3.6 = 1.2 von Mc aus abtragen
- 2/3 von 4.8 = 3.2 von A aus abtragen
- Schnittpunkt = Schwerpunkt S
- von Mc aus 3.6 abtragen = C
A
Mc
B
Lösung zu Aufgabe 5d)gabe 1
Seite a = 6 cm, Höhe hb = 5.6 cm, Seitenhalbierende sc = 4 cm
Skizze:
Konstruktion:
C
4
6
m
C
5.6
B'
B
Mc
A
KB:
sc
-Höhenstreifen 5.6 cm mit Mittelparallele m
- C wählen, 6 cm abtragen -> B, B'
- Von C aus 4 cm abtragen auf m -> Mc
- B Mc verlängern -> A, A'
A
Mc
B
A'
Lösung zu Aufgabe 5e)gabe 1
Seite a = 4.9 cm, Höhe hb = 4.2 cm, Höhe ha = 7.2 cm
Skizze:
C
Konstruktion:
P
7.2
4.9
4.2
C
B
A
P'
A'
P
B
KB:
-Höhenstreifen ha = 7.2 cm
- k(B, 4.2 cm) ∩ Thaleskreis = P
- CP verlängern → A
- Es gibt 2 Lösungen!
A