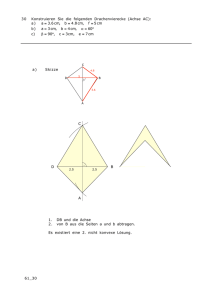
Lösungen zu Dreieckskonstruktionen 1 A B C

Lösungen zu Dreieckskonstruktionen 1
Mathematik
T. Hunziker, dipl. math., dipl. ML
www.hunziker.jimdo.com
Hilfsmittel: Geo-Dreieck, Lineal, Zirkel, Formelblatt GBMS
Okt 13
Achtung: Wichtige Infos zu Dreiecken finden Sie auch im Skript „Repetition: Geometrie, 1. Teil“.
Allgemeines zur Konstruktion mit Zirkel und Lineal
Die klassische Methode
Bei den antiken Griechen und bis ins 20. Jahrhundert wurden nur ein Zirkel und ein Lineal ohne
Markierungen benutzt - alles andere war strengstens verboten.
Ausnahmen im heutigen Schulunterricht
Ziehen eines 90°-Winkels mit dem Geodreieck
Abtragen eines vorgegebenen Winkels mit dem Geodreieck oder Winkelmesser
Ziehen einer Parallele mit Geodreieck und Lineal, oder nur mit einem Geodreieck
•
•
•
Verschiedene Lösungen
Es sind grundsätzlich alle verschiedenen Lösungen zu konstruieren, auch wenn in der Aufgabe steht:
„Konstruiere ein Dreieck ...“. Kongruente Lösungen sind aber von dieser Regel ausgenommen.
Skizze
Die Skizze oder Planfigur ist eine nicht massstabgetreue
Zeichnung der Figur, die konstruiert werden soll.
Z.B. : a = 4 cm, b = 3 cm, γ = 75°
Tip: gegebene Grössen mit Farbe einzeichnen.
Eine Skizze ist nicht zwingend vorgeschrieben, wird aber
dringend empfohlen.
Konstruktionsbericht (KB)
Es gibt keine verbindlichen Regeln für Konstruktionsberichte. Hier sind zwei verschiedene
Konstruktionsberichte für ein und dieselbe Dreieckskonstruktion.
Konstruieren Sie ein Dreieck ABC mit Seite a = 3 cm, Seite b = 4 cm und Seite c = 5 cm.
KB (Variante 1)
KB (Variante 2)
- Zeichne Strecke AB mit
Länge 5cm
- Von A aus 4 cm abtragen
- Von B aus 3 cm abtragen
- Schnittpunkt = C
- Verbinden
- AB = 5 cm
- k(A, 4 cm)
∩
C
Konstruktion
k(B, 3cm) = C
B
A
Zu jeder Konstruktion ist ein kurzer Konstruktionsbericht (KB) zu schreiben!
Spezielle Tipps bei Dreieckskonstruktionen
•
Lernen Sie die folgenden Bezeichnungen (mehr Infos im Skript „Repetition: Geometrie, 1.Teil“):
hb = Höhe auf die Seite b
sa = Seitenhalbierende der Seite a
•
•
•
wγ = Winkelhalbierende des Winkels
mb = Mittelsenkrechte der Seite b
γ
Wenn eine Höhe bekannt ist, beginnen Sie mit dem Höhenstreifen.
Wenn der Umkreisradius bekannt ist, beginnen Sie mit dem Umkreis.
Wenn eine Seitenhalbierende gegeben ist, kann es nützlich sein zu beachten, dass der
Schwerpunkt die Seitenhalbierende immer im Verhälnis 2:1 teilt.
Lösungen
Seite 2 von 4
Dreieckskonstruktionen 1
Aufgabe 1 (Übung)
Beim Anfertigen einer Skizze ist es oft am besten, ein möglichst „unregelmässiges“ Dreieck zu
zeichnen. Zeichnen Sie zwei Dreiecke, die weder gleichseitig, gleichschenklig noch rechtwinklig
aussehen. Messen Sie zur Kontrolle alle Seiten und Winkel!
a) Ein spitzwinkliges
b) Ein stumpfwinkliges
63°
2 cm
4.3 cm
3 cm
101°
3.1 cm
50°
75°
29°
4 cm
42°
4 cm
Aufgabe 2
Konstruieren Sie ein Dreieck mit Seite a = 3 cm, Seite c = 6 cm und Seitenhalbierende sa = 5 cm.
Skizze:
Konstruktion:
C
C
3 cm
5
cm
A
Ma
Ma
A
B
6 cm
B
KB:
Strecke AB = 6 cm
Von A aus 5 cm, von B aus 1.5 cm --> Punkt Ma
BMa verdoppeln --> Punkt C
•
•
•
Aufgabe 3
Konstruieren Sie ein Dreieck mit Seite c = 5 cm, Umkreisradius r = 3 cm und Winkel β = 70°.
Skizze:
Konstruktion:
C
C
M
3
3
70°
A
5
KB:
•
•
•
M, Umkreis 3 cm
A wählen, 5cm --> B
70°-Winkel bei B --> C
B
M
A
B
Lösungen
Aufgabe 4
Seite 3 von 4
Dreieckskonstruktionen 1
Konstruieren Sie ein Dreieck mit Höhe hc = 4 cm, Winkelhalbierende wγ = 4.5 cm und Winkel γ = 38°.
Skizze:
Konstruktion:
C
C
68°
19°
19°
4
4.5
4
B
A
KB:
Höhenstreifen 4 cm, C wählen
•
wγ = 4.5 cm
•
Auf beiden Seiten 19° abmessen --> A,B
B
A
•
Aufgabe 5
Konstruieren Sie ein gleichschenkliges Dreieck (Basis = c) mit Höhe hb = 2.9 cm und Seite b = 3.5 cm.
Skizze:
Konstruktion:
C
B2
C
3.5
3.5
2.9
B
A
A
KB:
•
Höhenstreifen 2.9 cm
•
Strecke AC = 3.5 cm
•
Von C aus 3.5 cm --> B
•
(2 Lösungen)
B1
Aufgabe 6
Konstruieren Sie ein Dreieck mit Winkel β = 40°, Winkel γ = 65° und Winkelhalbierende wβ = 4.2 cm.
Skizze:
Konstruktion:
C
65°
C
P 95°
4.2
A
20°
40°
20°
P
20°
B
KB:
•
Strecke PB = 4.2 cm
•
Bei B auf beiden Seiten 20° abtragen
•
95° bei P --> C
•
PC verlängern --> A
95°
20°
A
B
Lösungen
Aufgabe 7
Seite 4 von 4
Dreieckskonstruktionen 1
Konstruieren Sie ein Dreieck mit Seite b = 4.5 cm, Seite c = 6 cm und Höhe ha = 4 cm.
Skizze:
Konstruktion:
C
C2
4.5
4
C1
B
6
A
B
A
KB:
Höhenstreifen 4 cm, Punkt A
k (A, 6 cm) --> B
k (A, 4.5 cm) --> C1,C2
2 Lösungen
•
•
•
•
Aufgabe 8
Konstruieren Sie ein Dreieck mit Seite b = 4.3 cm, Höhe hc = 4 cm und Seitenhalbierende sb = 5 cm.
Skizze:
Konstruktion:
C
4
C
4.3
5
A
B
KB:
•
Höhenstreifen 4 cm, Punkt C
•
Von C aus 4.3 cm --> A1,A2
•
Mittelpunkte P1,P2 konstruieren
•
Von P aus 5 cm --> B1,B2
•
2 Lösungen
P1
4
A1
P2
A2
B1
B2