Lösungen zu Kapitel 1

Lösungen zu Kapitel 1
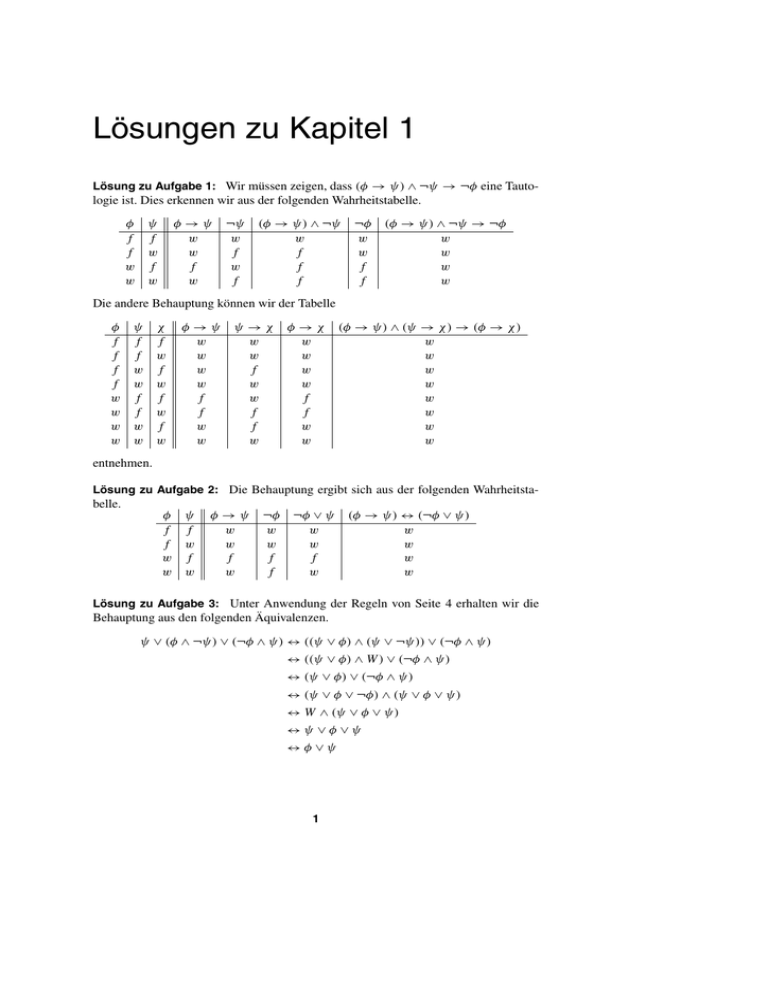
Lösung zu Aufgabe 1: Wir müssen zeigen, dass (φ → ψ) ∧ ¬ψ → ¬φ eine Tautologie ist. Dies erkennen wir aus der folgenden Wahrheitstabelle.
φ
f
f
w
w
φ→ψ
w
w
f
w
ψ
f
w
f
w
¬ψ
w
f
w
f
(φ → ψ) ∧ ¬ψ
w
f
f
f
¬φ
w
w
f
f
(φ → ψ) ∧ ¬ψ → ¬φ
w
w
w
w
Die andere Behauptung können wir der Tabelle
φ
f
f
f
f
w
w
w
w
ψ
f
f
w
w
f
f
w
w
χ
f
w
f
w
f
w
f
w
φ→ψ
w
w
w
w
f
f
w
w
ψ →χ
w
w
f
w
w
f
f
w
φ→χ
w
w
w
w
f
f
w
w
(φ → ψ) ∧ (ψ → χ ) → (φ → χ )
w
w
w
w
w
w
w
w
entnehmen.
Lösung zu Aufgabe 2: Die Behauptung ergibt sich aus der folgenden Wahrheitsta-
belle.
φ
f
f
w
w
ψ
f
w
f
w
φ→ψ
w
w
f
w
¬φ
w
w
f
f
¬φ ∨ ψ
w
w
f
w
(φ → ψ) ↔ (¬φ ∨ ψ)
w
w
w
w
Lösung zu Aufgabe 3: Unter Anwendung der Regeln von Seite 4 erhalten wir die
Behauptung aus den folgenden Äquivalenzen.
ψ ∨ (φ ∧ ¬ψ) ∨ (¬φ ∧ ψ) ↔ ((ψ ∨ φ) ∧ (ψ ∨ ¬ψ)) ∨ (¬φ ∧ ψ)
↔ ((ψ ∨ φ) ∧ W ) ∨ (¬φ ∧ ψ)
↔ (ψ ∨ φ) ∨ (¬φ ∧ ψ)
↔ (ψ ∨ φ ∨ ¬φ) ∧ (ψ ∨ φ ∨ ψ)
↔ W ∧ (ψ ∨ φ ∨ ψ)
↔ψ ∨φ∨ψ
↔φ∨ψ
1
2
Lösungen zu Kapitel 1
Lösung zu Aufgabe 4: Die neunzehn Behauptungen können durch Aufstellen der
entsprechenden Wahrheitstabellen bewiesen werden. Wir zeigen beispielhaft das erste
Distributivgesetz.
φ
f
f
f
f
w
w
w
w
ψ
f
f
w
w
f
f
w
w
χ
f
w
f
w
f
w
f
w
ψ ∧χ
f
f
f
w
f
f
f
w
φ∨ψ
f
f
w
w
w
w
w
w
φ∨χ
f
w
f
w
w
w
w
w
φ ∨ (ψ ∧ χ ) (φ ∨ ψ) ∧ (φ ∨ χ )
f
f
f
f
f
f
w
w
w
w
w
w
w
w
w
w
Da die beiden letzten Spalten identische Einträge enthalten, sind die zugehörigen Ausdrücke äquivalent.
Lösung zu Aufgabe 5: Man kann diese Aufgabe lösen, indem man entweder eine
Wahrheitstabelle aufstellt und anschließend wie im Buch beschrieben vorgeht oder indem man die Rechenregeln einer Boole’schen Algebra anwendet. Man erhält in beiden
Fällen (bis auf die Reihenfolge der Teilausdrücke) die folgenden Lösungen:
Disjunktive Normalform:
Konjunktive Normalform:
x yz + x ȳz + x ȳ z̄ + x y z̄ + x̄ y z̄
(x + y + z)(x + y + z̄)(x + ȳ + z̄)
Lösung zu Aufgabe 6: Die folgenden Aussagen sind jeweils äquivalent, was wir
durch das Symbol ⇔ ausdrücken:
φ1 ∧ . . . ∧ φ n ⇒ ψ
⇔ Für alle Belegungen F gilt F(φ1 ∧ . . . ∧ φn → ψ) = w.
(∗)
⇔ Für alle Belegungen F mit F(φ1 ∧ . . . ∧ φn ) = w gilt F(ψ) = w.
⇔ Für alle Belegungen F gilt: Wenn für alle i, i = 1, . . . , n, F(φi ) = w ist,
dann ist F(ψ) = w.
⇔ 8 |= ψ.
(∗)
Wir zeigen die Äquivalenz ⇔, die anderen ergeben sich sofort aus den Definitionen
(∗)
von ⇒, ∧ und |=. Zum Nachweis der ⇒-Richtung von ⇔ sei eine Belegung F mit
F(φ1 ∧. . .∧φn ) = w gegeben. Mit der Voraussetzung folgt F(ψ) = w. Zum Nachweis
der ⇐-Richtung müssen wir F(φ1 ∧ . . . ∧ φn → ψ) = w für alle Belegungen F zeigen.
Es sei eine Belegung F gegeben. Falls F(φ1 ∧ . . . ∧ φn ) = f ist, gilt die Behauptung
trivialerweise, für F(φ1 ∧ . . . ∧ φn ) = w folgt sie aus der Voraussetzung.
Lösungen zu Kapitel 1
3
Lösung zu Aufgabe 7: Für die Sheffer-Funktion | gelten x + y ⇔ (x | x) | (y | y)
und x y ⇔ (x | y) | (x | y). Wenn wir dies in die Gleichung für c einsetzen, erhalten
wir
c ⇔ yz + x z + x y
⇔ ((yz | yz) | (x z | x z)) + x y
⇔ (((yz | yz) | (x z | x z)) | ((yz | yz) | (x z | x z))) | (x y | x y).
Wenn wir im letzten Ausdruck yz durch (y | z) | (y | z), x z durch (x | z) | (x | z)
und x y durch (x | y) | (x | y) ersetzen, bekommen wir den gesuchten Ausdruck.
Für die Peirce-Funktion ↓ gelten entsprechend x + y ⇔ (x ↓ y) ↓ (x ↓ y) und
x y ⇔ (x ↓ x) ↓ (y ↓ y). Wenn wir diese Äquivalenzen auf yz + x z + x y anwenden,
erhalten wir den verlangten Ausdruck.
Lösung zu Aufgabe 8: Wir müssen beweisen, dass der Ausdruck φ → (ψ → (χ →
φ)) mithilfe des Kalküls K hergeleitet werden kann. Durch Aufstellen einer Wahrheitstabelle überprüft man, dass φ → (ψ → (χ → φ)) allgemeingültig ist. Aus der Bemerkung im Anschluss an Satz 1.2 folgt hieraus die Behauptung.
Lösung zu Aufgabe 9: Die folgenden Aussagen sind jeweils äquivalent, was wir
durch das Symbol ⇔ ausdrücken:
8 |= φ ⇔ Für jede Interpretation I gilt:
Wenn I ein Modell von 8 ist, dann ist I ein Modell von φ.
⇔ Es gibt keine Interpretation I, die ein Modell von 8 ∪ {¬φ} ist.
⇔ Die Ausdrucksmenge 8 ∪ {¬φ} ist nicht erfüllbar.
Für 8 = ∅ bedeutet dies, dass ein Ausdruck φ genau dann allgemeingültig ist, wenn
¬φ nicht erfüllbar ist.
4
Lösungen zu Kapitel 1
Lösung zu Aufgabe 10: Zur Beschreibung einer Boole’schen Algebra wählen wir
S = {F, W, ¬, ∧, ∨}. Hierin sind F und W Konstanten. Bei ¬ handelt es sich um
ein einstelliges und bei ∧ und ∨ um zweistellige Funktionssymbole, die die folgenden
Axiome erfüllen:
φ ∨ ψ = ψ ∨ φ,
φ ∧ ψ = ψ ∧ φ,
(φ ∨ ψ) ∨ χ = φ ∨ (ψ ∨ χ ),
(φ ∧ ψ) ∧ χ = φ ∧ (ψ ∧ χ ),
φ ∨ (ψ ∧ χ ) = (φ ∨ ψ) ∧ (φ ∨ χ ),
φ ∧ (ψ ∨ χ ) = (φ ∧ ψ) ∨ (φ ∧ χ ),
φ ∨ (φ ∧ ψ) = φ,
φ ∧ (φ ∨ ψ) = φ,
φ∨W
φ∧W
φ∨F
φ∧F
φ ∨ ¬φ
φ ∧ ¬φ
= W,
= φ,
= φ,
= F,
= W,
= F.
Lösung zu Aufgabe 11: Die folgenden Ausdrücke sind Aussagen über positive natürliche Zahlen. Die Funktionssymbole +, −, · und / bedeuten die Addition, die Subtraktion, die Multiplikation und die Division.
(a) ∀m∀n. ¬((m · m)/(n · n) = 5)
(b) ∀n∃k. 2 · n · n · n + 3 · n · n + n = 2 · k
(c) ∀n∃k. n · n · n − n = 3 · k
(d) ∀m∀n. (∃k. mn = 2k → (∃l. m = 2l) ∨ (∃o. n = 2o))
(e) ∀n. ((∀m. ¬(n = 2m)) ↔ (∃l. 3n + 1 = 2l))
Lösungen zu Kapitel 1
5
Lösung zu Aufgabe 12:
(a) Wir zeigen zunächst die folgende Hilfsaussage: Für alle natürlichen Zahlen p
gilt: Wenn p 2 durch 5 teilbar ist, dann ist auch p durch 5 teilbar.
Wir zeigen die Hilfsaussage indirekt. Dazu nehmen wir an, dass p nicht durch 5
teilbar ist. Wir können dann p in der Form p = 5l + q mit 1 ≤ q ≤ 4 schreiben.
Hieraus folgt p 2 = 25l 2 + 10lq + q 2 . Da 1, 4, 9 und 16 nicht durch 5 teilbar sind,
ist auch p 2 nicht durch 5 teilbar.
Die Aussage
√ der Aufgabe soll jetzt indirekt bewiesen werden. Wir nehmen also
an, dass 5 rational ist. Dann gibt es natürliche Zahlen n und m, m 6 = 0, mit
√
5 = mn .
Wir können voraussetzen, dass n und m bereits gekürzt sind. Durch Quadrieren
dieser Gleichung bekommen wir
5m 2 = n 2 .
Es folgt, dass n 2 durch 5 teilbar ist. Dann muss nach der Hilfsaussage auch n =
5k durch 5 teilbar sein. Wir erhalten
5m 2 = (5k)2 = 25k 2
und hieraus
m 2 = 5k 2 .
(b)
(c)
(d)
(e)
Die letzte Aussage impliziert, dass m 2 und damit auch m durch 5 teilbar ist. Damit
sind sowohl n als auch m durch 5 teilbar, ein Widerspruch zu der Tatsache, dass
diese Zahlen als gekürzt angenommen werden konnten.
Wir zeigen die Aussage durch eine Fallunterscheidung. Falls n = 2k gerade ist,
dann ist auch 2n 3 + 3n 2 + n = 2(2k)3 + 3(2k)2 + 2k = 16k 3 + 12k 2 + 2k gerade.
Falls n = 2k + 1 ungerade ist, dann ist 2n 3 + 3n 2 + n = 2(2k + 1)3 + 3(2k +
1)2 + (2k + 1) = 2(2k + 1)3 + 12k 2 + 12k + 3 + 2k + 1 gerade.
Wir zeigen diese Aussage durch eine Fallunterscheidung.
1. Fall: n = 3k für eine natürliche Zahl k.
Die Zahl n 3 − n = 27k 3 − 3k = 3(9k 3 − k) ist durch 3 teilbar.
2. Fall: n = 3k + 1 für eine natürliche Zahl k.
Die Zahl n 3 − n = (3k + 1)3 − (3k + 1) = 27k 3 + 27k 2 + 6k ist durch 3 teilbar.
3. Fall: n = 3k + 2 für eine natürliche Zahl k.
Die Zahl n 3 − n = (3k + 2)3 − (3k + 2) = 27k 3 + 54k 2 + 33k + 6 ist durch 3
teilbar.
Da das Produkt zweier ungerader Zahlen ungerade ist, folgt die Aussage sofort
durch Kontraposition.
Diese Aussage wird durch einen Äquivalenzbeweis gezeigt. Es sei eine natürliche
Zahl n gegeben. Wir setzen zunächst voraus, dass n ungerade ist, das heißt n =
2k + 1 für eine natürliche Zahl k. Dann ist 3n + 1 = 3(2k + 1) + 1 = 6k + 4
gerade. Falls 3n + 1 gerade ist, gibt es eine natürliche Zahl l mit 3n + 1 = 2l.
Die Zahl 3n = 2l − 1 ist also ungerade. Damit ist auch n ungerade.
6
Lösungen zu Kapitel 1
Lösung zu Aufgabe 13: Die Aussage (a) gilt nicht, da beispielsweise 1 2 + 32 = 10
keine Quadratzahl ist. Das Produkt zweier Quadratzahlen n = k 2 und l = p 2 ist wegen
nl = k 2 p2 = (kp)2 ) stets eine Quadratzahl. Dies beweist (b).
Lösung zu Aufgabe 14: Wir definieren die Funktion log2 :
→
∀x ∀y. log2 (x) = y ↔ 2 y ≤ x < 2 y+1 .
durch
(*)
Um die Zulässigkeit dieser Definition nachzuweisen, müssen wir zeigen, dass es zu jeder natürlichen Zahl x genau eine natürliche Zahl y gibt, die (*) erfüllt. Dazu betrachten
wir die Menge
M = {n | x < 2n }.
M enthält unendlich viele Elemente, das heißt, M ist nichtleer. Jede nichtleere Menge
von natürlichen Zahlen besitzt ein kleinstes Element. Das von M sei t. Wir wählen
dann y als t − 1. Offenbar gelten 2 y = 2t−1 ≤ x und x < 2t = 2 y+1 , das heißt,
y erfüllt die Bedingung (*). Zum Nachweis der Eindeutigkeit nehmen wir an, dass es
zwei natürliche Zahlen y1 und y2 gibt, die (*) erfüllen. Aus der Bedingung folgt dann
2 y1 ≤ x < 2 y2 +1
und daraus y1 ≤ y2 . Genauso erhalten wir y2 ≤ y1 . Aus beiden Aussagen zusammen
folgt y1 = y2 .
Lösung zu Aufgabe 15:
Algorithmus (Berechnung des ganzzahligen Logarithmus)
Eingabe: x ≥ 1.
Ausgabe: y = log2 x, das heißt 2 y ≤ x < 2 y+1 .
begin
t := 1;
y := 0;
{Schleifeninvariante: t = 2 y ∧ t ≤ 2x ∧ x ≥ 1}
while t ≤ x do
t := 2 ∗ t;
y := y + 1
od
y := y − 1
end
Die partielle Korrektheit ergibt sich aus der angegebenen Schleifeninvarianten. Die totale Korrektheit erhält man aus der Tatsache, dass die Folge t1 , t2 , t3 , . . . der Werte,
die die Variable t annimmt, streng monoton steigend ist. Für ein i, i ≥ 1, wird deshalb
ti > x.
Lösungen zu Kapitel 1
Lösung zu Aufgabe 16:
(a) Die Anfrage an den Prolog-Interpreter und die Ausgabe lauten:
| ?- mutter(X,golo).
X = katia ? ;
(b) Die Anfrage an den Prolog-Interpreter und die Ausgabe lauten:
|
X
Y
X
Y
X
Y
X
Y
X
Y
X
Y
X
Y
X
Y
X
Y
?- mutter(X,Y).
= julia
= heinrich ? ;
= julia
= thomas ? ;
= maria
= carla ? ;
= katia
= erika ? ;
= katia
= klaus ? ;
= katia
= golo ? ;
= katia
= monika ? ;
= katia
= elisabeth ? ;
= katia
= michael
Lösung zu Aufgabe 17: Die Fakten lauten:
maennlich(johann).
maennlich(heinrich).
maennlich(thomas).
maennlich(klaus).
maennlich(golo).
maennlich(michael).
weiblich(erika).
weiblich(carla).
weiblich(monika).
weiblich(elisabeth).
weiblich(julia).
weiblich(maria).
weiblich(katia).
Mögliche Regeln zur Definition der Schwester- und der Cousin-Beziehung lauten:
schwester(X,Y) :- geschwister(X,Y),weiblich(X).
cousin(X,Y) :- maennlich(X),vater(A,X),vater(B,Y),geschwister(A,B).
Um die Vorfahren-Relation auszudrücken, benötigen wir die folgenden vier Regeln:
vorfahre(X,Y)
vorfahre(X,Y)
vorfahre(X,Y)
vorfahre(X,Y)
::::-
mutter(X,Y).
vater(X,Y).
mutter(X,Z), vorfahre(Z,Y).
vater(X,Z), vorfahre(Z,Y).
7