Symbole und Formeln der Elektrodynamik

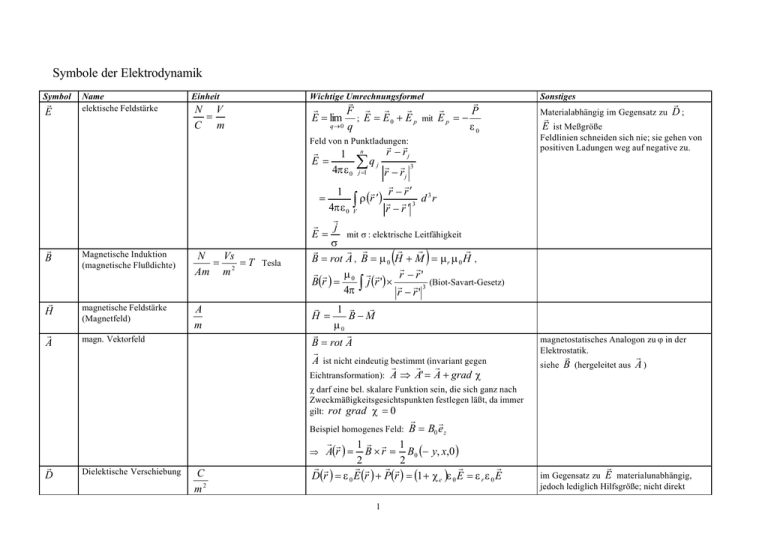
Symbole der Elektrodynamik
Symbol
r
E
r
B
r
H
r
A
Name
elektische Feldstärke
Einheit
N V
=
C m
Magnetische Induktion
(magnetische Flußdichte)
N
Vs
= 2 = T Tesla
Am m
magnetische Feldstärke
(Magnetfeld)
A
m
magn. Vektorfeld
Wichtige Umrechnungsformel
r
r
r
r
r
F r r
P
E = lim ; E = E 0 + E p mit E p = −
q→ 0 q
ε0
Sonstiges
Feld von n Punktladungen:
Feldlinien schneiden sich nie; sie gehen von
positiven Ladungen weg auf negative zu.
r r
r
r − rj
1 n
E=
∑q j r r 3
4πε 0 j =1
r − rj
r r
1
r r − r′ 3
=
ρ (r ′) r r 3 d r
4πε 0 ∫V
r −r′
r
r j
E=
mit σ : elektrische Leitfähigkeit
σ
r r
r
r
r r
B = rot A , B = µ 0 H + M = µ r µ 0 H ,
r r
rr
µ0 r r
r − r'
B(r ) =
j (r ') × r r 3 (Biot-Savart-Gesetz)
4π ∫
r − r'
(
Materialabhängig im Gegensatz zu
r
E ist Meßgröße
r
D;
)
r
1 r r
H =
B−M
µ0
r
r
B = rot A
r
A ist nicht eindeutig bestimmt (invariant gegen
r
r r
Eichtransformation): A ⇒ A' = A + grad χ
magnetostatisches Analogon zu ϕ in der
Elektrostatik.
siehe
r
r
B (hergeleitet aus A )
χ darf eine bel. skalare Funktion sein, die sich ganz nach
Zweckmäßigkeitsgesichtspunkten festlegen läßt, da immer
gilt: rot grad χ = 0
Beispiel homogenes Feld:
r
r
B = B0 e z
r r 1 r r 1
A(r ) = B × r = B0 (− y, x,0 )
2
2
r r
r r r r
r
r
D(r ) = ε 0 E (r ) + P(r ) = (1 + χ e )ε 0 E = ε r ε 0 E
⇒
r
D
Dielektische Verschiebung
C
m2
1
r
im Gegensatz zu E materialunabhängig,
jedoch lediglich Hilfsgröße; nicht direkt
meßbar
ϕ
skalares elektrisches
Potential
Nm
= V Volt
As
r
D& : Verschiebungsstrom
r r
r
E (r ) = −∇ϕ (r )
r
r r r
r
r
U = ϕ(r ) − ϕ(r0 ) = ∫ E (r ') d r '
Potentialdifferenz zwischen zwei Punkten
bezeichnet man als Spannung U
r0
r
ϕ(r ) =
1
4πε 0
∫
r
ρ (r ') 3
r r d r'
r − r'
r
r r
r
Vereinbarung: ϕ (r ) = −∫ E (r ') dr '
∞
ρ
Raumladungsdichte
C
m3
r 3
∆Q dQ
ρ = lim
=
; Q = ∫ ρ (r )d r
∆V →0 ∆V
dV
V
Q 1
r
Mittlere Raumladungsdichte: ρ =
= ∫ ρ (r )dV
V VV
r
r r
Punktladung: ρ (r ) = qδ (r − r0 )
σ
Flächenladungsdichte
C
m2
∆Q dQ
σ = lim
=
∆A → 0 ∆ A
dA
Linienladungsdichte
λ
(auch κ)
C
m
q, Q
Ladung
A
= C (Coulomb)
s
r
F
Coulomb-Kraft
N
Q 1
r
Mittlere Flächenladungsdichte: σ =
= ∫ σ (r )dA
A AA
∆Q dQ
λ = lim
=
∆s → 0 ∆s
ds
Q 1
r
Mittlere Flächenladungsdichte: λ =
= ∫ λ (r )ds
s ss
r r
n
r1 − r j
1
n Punktladungen: F1 =
∑q j r r 3
4πε0ε r j= 2
r1 − r j
r
r
F = q⋅ E
(
)
)
r
r r
σ = n ⋅ Da − Di nur Überschußladungen
r
r r
σ p = n ⋅ Pa − Pi Polarsisationsladungen
(
ist konservativ, besitzt also ein Potential:
r
r
F = −∇V mit V = q ⋅ ϕ(r )
2
r
p
r
P
Dipolmoment
C ⋅m
r
r r
p = ∫ r ρ (r ) d 3 r
Zeigt von negativen zu positiven Ladungen
Zwei Punktladungen -q und +q im Abstand a:
Polarisation
As
m2
r
r
P = χ e ε 0 E (isotrope Medien)
r r
1
r
P(r ) = r ∑ p j
v (r ) j∈v
r
r
p = q ⋅a
Kennzeichnet die Dichte der
Polarisationsladungen;
Durch Polarisation können Ladungen auch
auf Nichtleiter Kräfe ausüben.
mit p Dipolmoment eines Teilchens im Volumen v
P
r
j
Leistung
magnetisches Moment
r
M
Magnetisierung
µ0
χe
P=
r r r r 3
∫ j (r ) ⋅ E (r )d r
V
Stromdichte
m
r
M
ε0
W
Drehmoment
C
A
= 2
2
s⋅m
m
r
r r r
∂ρ
r
div j = −
, I = ∫ j ⋅ df ; j = ρ v
∂t
F
r
r
j = σ E mit σ : elektrische Leitfähigkeit
1
r r r
m = ∫ d 3 r r × j (r )
2
r
r
bei isotropem, linearen Medium: M = χ m H
[
A
m
Nm
Dielektrizitätskonstante
(elektrische Feldkonstante)
As
Vm
Magnetische Feldkonstante Vs
Am
Ladung die je Zeiteinheit durch die
Flächeneinheit senkrecht zur Stromrichtung
transportiert wird.
]
r
r r
r r
M = m × B (= r × F )
1
As
ε0 =
= 8,854187871 ⋅10 −12
2
µ 0c
Vm
Vs
Vs
µ 0 = 4π ⋅ 10 −7
≈ 1,256637 ⋅ 10 − 6
Am
Am
mittleres magnetisches Moment pro Volumen
nicht zu verwechseln mit der Magnetisierung
χe = 0
elektrische Suszeptibilität
1
Nicht polarisierbare Medien haben
χm
magnetische Suszeptibilität
1
Nicht magnetisierbare Medien haben
εr
relative
Dielektrizitätskonstante
(Permittivitätszahl)
1
relative Permeabilität
1
µr
χm = 0
ε r = 1 + χ e = (n + jκ )
2
n : Brechzahl; κ : Absorbtionskoeffizient, (Stöcker S.
786/410, Koeffizient, der Absorbtion, Streuung und
induzierte Emission in einem Medium beschreibt(?))
j : imaginäre Einheit
µr = 1 + χ m
3
ε
Permittivität
I
elektrischer Strom
R
Widerstand
U
elektrische Spannung
G
elektr. Leitwert
b
Beweglichkeit von
Ladungsträgern
ρ
spezifischer Widerstand
κ
auch
σ
elektr. Leitfähigkeit
S
m
C
Kapazität
F=
As
Vm
C
= A (Ampere)
s
V
Ω = (Ohm)
A
V (Volt)
ε = ε0 ⋅εr
U
I
U = RI
r r
& = − LI&
U ind = ∫ E ⋅ dr = −Φ
R=
siehe auch unter ϕ (el. Potential)
C
1
= S (Siemens)
Ω
m2
Vs
1
I
G= =
R U
v v ⋅l
b= =
;
E
U
v : mittlere Driftgeschwindigkeit
E : elektr. Feldstärke; U : Spannungsabfall
Ωm
l
1
, ρ =
A
κ
κ = ρ ⋅ b (Ladungsträgerdichte * Beweglichkeit)
1 l
R=
,
κ A
1
κ=
ρ
R=ρ
C
(Farad)
V
Q
C = ; Plattenkondensator:
U
C =
ε 0ε
materialabhängige Größe;
unabhängig von der Geometrie des Leiters
Bei Bezeichnung mit σ darf dies natürlich
nicht mit der Flächenladungsdichte
verwechselt werden
Die Kapazität eines Kondensators wird durch
das Einbringen eines Dielektrikums zwischen
die Kondensatorplatten gesteigert um ε r .
Die elektrische Feldstärke verringert sich um
1
.(???)
εr
L
(Selbst-)Induktivität
H =
Vs
(Henry)
A
Induktivität einer Spule:
L = n2 Λ m
mit n : Windungszahl und Λm : magnetischer Leitwert
4
Siehe auch Induktionsfluß!
1H ist eine große Einheit, gebräuchliche
Induktivitäten liegen im Bereich 1µH-1H
Λm
magnetischer Leitwert
H =
Vs
(Henry)
A
magn. Leitwert einer Ringspule:
Λ m = µ 0µ r
A
l
mit A : Querschnitsfläche
l : mittlere Feldlinienlänge
Rm
magnetischer Widerstand
1/H
ψ
Induktionsfluß
Wb=Vs (Weber)
φ
magnetischer Fluß
Wb=Vs (Weber)
1
Λm
Ψ = LI = nφ mit n : Anzahl Spulenwindungen
r r
φ = ∫ B ⋅ dA
Rm =
A
Von Geometrie und Permeabilität des
magnetischen Kreises abhängig. Für
Spulenkerne vom Hersteller angegeben.
Kehrwert des magnetischen Leitwerts.
Wird bei der Berechnung magnetischer
Kreise verwendet. Siehe auch Induktivität
Maxwellgl.:
φ=
r r
B
∫ ⋅ dA ≡ 0
∂V
(magnetische Quellenfreiheit)
we
Energiedichte des el. Feldes
Wm
magnetische Feldenergie
J
m3
J
∆W e
=
∆V →0 ∆V
we = lim
elektrostat. Feldenergie
J
Energiestromdichte
=Poynting-Vektor
W/m2
r
0
1
∑ Lij I i (t ) I j (t )
2 i, j
1 2
spezialfall eines einzelnen Leiterkreises: W m = LI
2
A
A
r r
W AB = −q ∫ E ⋅ dr = q ∫ dϕ = q ⋅ U AB
B
r
S
r
∫ E ⋅ dD
r r
µ r µ0
j ⋅ j'
3
3
Wm =
d r ∫ d r' r r
∫
8π
r − r'
Fadenförmige Leiter:
W AB
Dmax
Wm =
Die Arbeit wird positiv gezählt, wenn sie am
System geleistet wird.
B
1
r r
W = ∫ ρ (r )ϕ(r ) d 3r
2
1 r r 3
Dielektrikum: W = ∫ E ⋅ D d r
2
r r r
Gibt den Betrag und Richtung des
S = E×H
Enegietransportes in elektromagnetischen
1 r r
Feldern an.
=
E × B ( nur für isotrope, lineare Medien )
µ rµ 0
Pro Zeiteinheit durch eine Fläche A transportierte Energie:
5
r r
dW
= ∫ S ⋅ dA
dt
A
Für freie elektromagnetische Wellen gilt:
r c
S = ( we + wm ) mit w x : Energiedichte
2
6