Elektrotechnik 2 - Studentenportal
Werbung
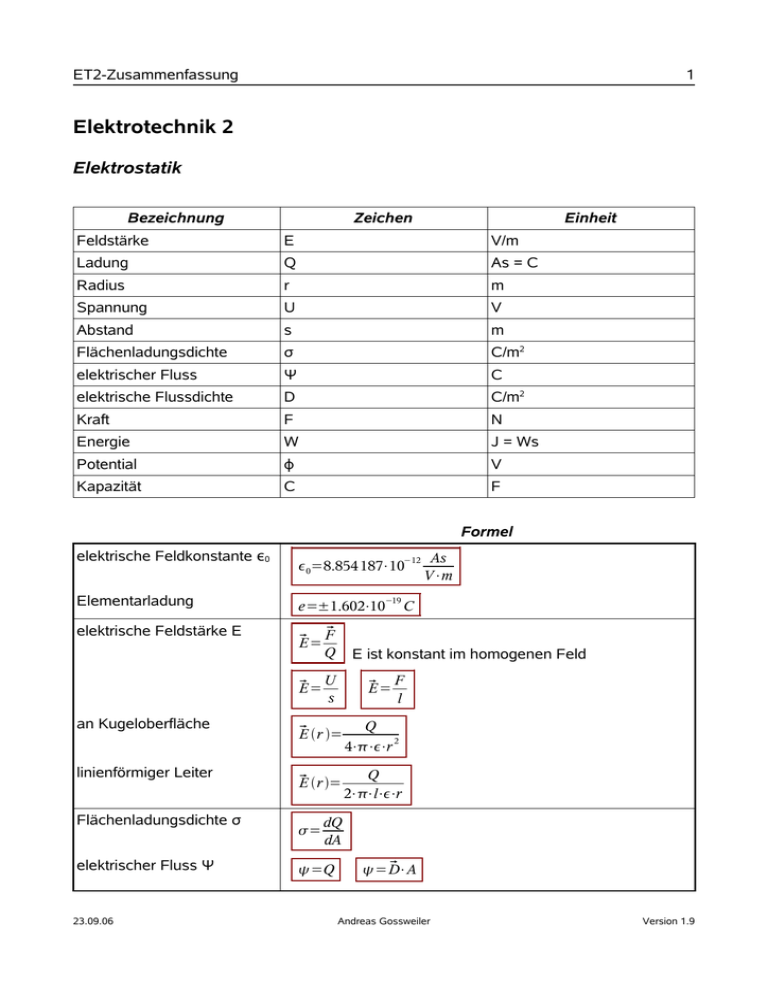
ET2-Zusammenfassung 1 Elektrotechnik 2 Elektrostatik Bezeichnung Zeichen Einheit Feldstärke E V/m Ladung Q As = C Radius r m Spannung U V Abstand s m Flächenladungsdichte σ C/m2 elektrischer Fluss Ψ C elektrische Flussdichte D C/m2 Kraft F N Energie W J = Ws Potential φ V Kapazität C F Formel elektrische Feldkonstante ε0 −12 0=8.854 187⋅10 Elementarladung e=±1.602⋅10 elektrische Feldstärke E F E= Q linienförmiger Leiter Flächenladungsdichte σ elektrischer Fluss Ψ 23.09.06 F E= l E r = Q 2 4⋅⋅⋅r E r = Q 2⋅⋅l⋅⋅r = C E ist konstant im homogenen Feld U E= s an Kugeloberfläche −19 As V⋅m dQ dA =Q ⋅A = D Andreas Gossweiler Version 1.9 ET2-Zusammenfassung 2 Formel elektrische Flussdichte D =⋅ D E =Q D A Ladung Q Q=C⋅U Q= I⋅t Kapazität Plattenkondensator C= zwischen 2 langen dünnen Leitern C= Konzentrische Zylinder C= ⋅A d ⋅⋅l d −r ln r oder für d >> r r a⋅r i 4⋅⋅ C=4⋅⋅⋅ = r a−r i 1 1 − r1 ra Kraft auf eine Punktladung F =Q⋅E Gesammt Kraft auf eine Elektrode Energie im Kondensator Potential φ parallele lange Leiter Spannung Kondensator laden mit konstanter Spannung 23.09.06 = F ⋅⋅l d ln r 2⋅⋅⋅l ra ln ri Konzentrische Kugeln zwischen 2 Punktladungen C= + Q F Q 1⋅Q 2 1 ⋅ 2 4⋅⋅ r 2 F ges = D ⋅A 2⋅ 2 1 Q 1 2 W = ⋅C⋅U = = ⋅Q⋅U 2 2⋅C 2 = = A Q 4⋅⋅⋅r = W ⋅ds =−∫ E Q 0 R0 Q ⋅ln 2⋅⋅⋅l r R0 Abstand Ladungsbezugspunkt r Abstand zur Ladung A B B A ⋅ds=∫ E ⋅ds U = B − A =−∫ E [ uc =U⋅ 1−e −t ] Andreas Gossweiler Version 1.9 ET2-Zusammenfassung 3 Formel −t i=I 0⋅e mit Konstantstrom U= Zeitkonstante τ I⋅t C = R⋅C Magnetische Felder Bezeichnung Zeichen Einheit magnetische Feldstärke H A/m magnetische Flussdichte (Induktion) B Vs/m2 = T magnetischer Fluss Φ Vs = Wb Spulenfluss Ψ Vs = Wb Durchflutung Θ A magnetische Spannung Vmagn A Induktivität L Vs/A = H Geschwindigkeit υ m/s magnetischer Widerstand Rmagn 1/H Drehmoment M Nm Kraft pro Fläche σ N/m2 Formel induktions Konstante magnetische Feldstärke (gerader Leiter) Innere Feldstärke Äussere Feldstärke auf der Kreisachse 23.09.06 0=4⋅⋅10 = H −7 Vs −6 Vs ≈1 , 257⋅10 Am Am I 2⋅⋅r 0 I H i= ⋅r 2 2⋅⋅r 0 H a= I 1 ⋅ 2⋅ r I H(r) r0 r I ⋅sin3 ∣H∣= d Andreas Gossweiler Version 1.9 ET2-Zusammenfassung 4 mitten in der Schleife für α=π/2 ∣H∣= I d in der Ringspule (Toroid) ∣H∣= N⋅I N⋅I = l 2⋅⋅r Zylinder Spule r H= N⋅I l H Koaxialer Zylinder (Koaxialkabel) H= I 2⋅⋅r + + + + + + + + magnetische Flussdichte (Induktion) B = H mit 2 Querschnitten BFe magnetischer Fluss B2 = B= A bei lL << lE gilt BL = BE B 1⋅A1 A2 [ B Fe = 0⋅⋅ −H Fe l Fe ] = l Fe ll b =∫ Br ⋅dA=B⋅A =I⋅L dA =l⋅dr a Spulenfluss =N⋅ Durchflutung mit Luftspalt =H Eisen⋅l Eisen H Luft⋅l Luft Durchflutung =I⋅N =∑ H⋅l magnetischer Widerstand magnetischer Leitwert magnetische Spannung μreff Länge des Luftspaltes Induktivität 23.09.06 R magn= = l = 0⋅r⋅A 1 R magn = V magn= H⋅l re = BE H E⋅0 = l L= l E⋅re −reff reff ⋅re L= N⋅ l L= lE lL N2 R magn Andreas Gossweiler reff = ⋅re re L I = I Version 1.9 ET2-Zusammenfassung in der Zylinderspule im Koaxialkabel Kraft im magnetischen Feld: Ladung bewegt sich normal zur Feldstärke 5 ⋅N 2⋅A L≈ l L= [ ] ra ⋅l ln 2⋅ ri ∣=Q⋅⋅B ∣F A L⋅B 2L F= 2⋅0 0⋅A⋅H 2 2 Gerader Leiter normal zur Feldstärke ∣=I⋅l⋅B ∣F zwischen zwei parallelen Leitern ∣= ∣F Drehmoment ∣= A⋅I⋅B⋅sin ∣M Kraft pro Fläche Wellenwiderstand Füllfaktor 23.09.06 ⋅l I 1⋅I 2 ⋅ 2⋅ d = 1 1 2 2 ⋅B = ⋅⋅H 2 2⋅ Z= = Aeff Aeff =⋅A A =I⋅ M AxB L C Andreas Gossweiler Version 1.9