Magnetische-Feldstärke - ME-LRT

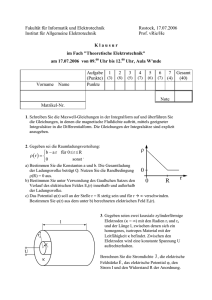
2. Aufgabe:
Gegeben ist folgende Leiteranordnung (Stromfluss I1 in positiver z-Richtung und
Stromfluss I 2 in negativer z-Richtung, beide unendlich lange dünne Leiter)
Berechnen Sie die magnetische Feldstärke H P1 im Punkt P1 (a, b) nach Betrag und
Richtung für diese Leiteranordnung!
Lösung:
Der Schlüssel zur Lösung ist die richtige Anwendung der Rechten-Hand-Regel.
Wenn durch einen Leiter ein Strom fließt, dann wird um diesen ein Magnetfeld
erzeugt. Dabei wird der Daumen in Stromrichtung gelegt und der Rest der Hand
umgreift den Leiter. Die Richtung der anderen Finger gibt die „Drehrichtung“ des
Magnetfeldes an.
Die bedeutet, dass am Punkt P1 die beiden Magnetfelder überlagert werden und sich
teilweise verstärken, oder abschwächen.
I
kann die magnetische Feldstärke berechnet
2r
werden. In diesem Fall ergibt sich r über den euklidschen Abstand zwischen den
Leitern und P1 .
I
H
2 a 2  b 2
Mit der allgemeinen Formel H 
Der zweite Teil der Aufgabestellung erfragt die Richtung der magnetischen
Feldstärke. Hierfür ist es wichtig, dass das B-Feld orthogonal auf dem
x
Abstandsvektor steht; d.h. wenn der Abstandsvektor d    ist, dann ist der
 y
 y 
 y 
orthogonale Vektor d    oder d    , je nach gesuchter Richtung.
 x 
 x 
Damit die Feldstärke einfach mit der Richtung multipliziert werden kann, muss der
Richtungsvektor ein Einheitsvektor sein; d.h. der Vektor muss noch durch den Betrag
geteilt werden:
 y 
1
| d |
2
2  x 
x y  
 b 
I1

2
2 
2(a  b )  a 
b
I2
Für den rechten Leiter bedeutet dies: H 2 
2
2  
2(a  b )  a 
Für den linken Leiter bedeutet dies: H1 
Da sich beide Felder problemlos überlagern, können beide aufaddiert werden.
H
 b 
 b   Hx 
I1
I2



  
2(a 2  b2 )  a  2(a 2  b2 )  a   H y 
Über den Zusammenhang B  0 H lässt sich das B-Feld bestimmen und mit diesem
die wirkenden Kräfte der Leiter aufeinender.
F
F  LI  B daraus ergibt sich die Kraft pro Längeneinheit mit  I  B
L
F1
I I 1
F
I I  1
 I1  B2  0 1 2   bzw. 2  I2  B1  0 1 2  
L
2·2a  0 
L
2·2a  0 