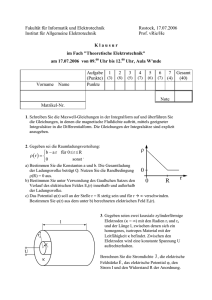
B= μ o I / (2πr)
Werbung

Berechnung der magnetischen Feldstärke mit Hilfe des Ampèreschen Durchflutungsgesetzes Biot-Savart-Gesetzes Inhalt Berechnung der magnetischen Feldstärke • • eines stromdurchflossenen Drahtes mit Hilfe des Ampèreschen Durchflutungsgesetzes eines Kreisstroms mit Hilfe des Biot-SavartGesetzes Magnetisches Feldes um einen Strom Der durch eine Fläche in Richtung ihrer Normalen fließende Strom I ist proportional zum Wirbelfeld um diese Fläche Magnetfeld und Strom B ds I B d s I 0 G . W eg 1 Tm2= 1 Wb Strom erzeugt ein magnetisches Wirbelfeld Stromdurchflossene, gerade Leiter sind von kreisförmigen, geschlossenen Feldlinien umgeben 0 I B 2 r I r 0 4 10 7 1T Magnetische Feldstärke um einen geraden Leiter 1A Stromstärke 1m Abstand vom Leiter 1 Vs/Am Magnetische Feldkonstante Magnetisches Feldes um einen Strom Die magnetische Feldstärke um einen stromdurchflossenen Draht nimmt proportional zum Abstand vom Draht ab Berechnung des Magnetfelds in der Mitte einer Kreisschleife mit Hilfe des Biot-Savart-Gesetzes r l 2r B I1 B 0 I1 2 r Das Biot-Savart Gesetz für parallele Leiterstückchen gleicher Länge mit Abstand r dl r d F 2 dl I1 I2 0 I 2 dl I1dl d F 2 4 r 2 d2F steht für einen „doppelt kleinen“ Kraftanteil von zwei kleinen Stücken dl Beitrag eines kurzen Leiterstücks zur magnetischen Feldstärke, in Analogie zur elektrischen Feldstärke Biot-Savart Gesetz Coulomb-Gesetz 0 I1dl1 I 2 dl2 d F 2 4 r q1 q2 F 2 40 r d 2 F I 2 dl2 dB F q2 E 2 0 I1dl1 dB 2 4 r 1 1 q1 E 2 40 r Annahme: dl senkrecht zu r, allgemein gilt dB~dl×r Magnetfeld eines Leiterstückchens im Abstand r dl r dB I1 0 I1dl dB 2 4 r Magnetfeld in der Mitte einer Kreisschleife dl r l 2r dB I1 B I1 0 dB 2 4 r I1dl B Umfang 2r dB 0 0 I1dl 0 I1 2 4 r 2 r Magnetfeld in der Mitte eines kreisförmig fließenden Stromes B 0 I 2 r I r 0 4 10 7 1T Magnetische Feldstärke in der Mitte der Stromschleife 1A Stromstärke 1m Radius der Stromschleife 1 Vs/Am Magnetische Feldkonstante Zusammenfassung • Für zwei Stromwege mit hoher Symmetrie wird die magnetische Feldstärke berechnet: – Strom im langen, geraden Draht, Feld im Abstand r : B= μo I / (2πr) – Strom in der Mitte einer kreisförmigen Leiterschleife mit Radius r : B= μo I / (2r) • Realisierungen des Kreisstroms: – Leiterschleifen in Spulen – Elektronenbahnen um den Kern Magnetfeld eines Elektrons auf einer Kreisbahn r l 2r B I1 Finis