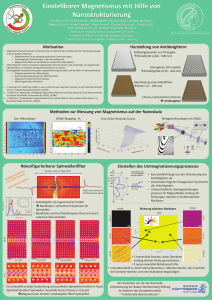
Bestimmung und Beeinflussung der Phaseneigenschaften von

Bestimmung und Beeinflussung der
Phaseneigenschaften von Spinwellen
in Yttrium-Eisen-GranatWellenleiterstrukturen
DIPLOMARBEIT
in
Experimentalphysik
von
Thomas Schneider
durchgeführt am
Fachbereich Physik
der Technischen Universität Kaiserslautern
unter Anleitung von
Prof. Dr. B. Hillebrands
Oktober 2005
. . . Geschwächt von Zeit und Schicksal, doch stark im Willen
”
Zu streben, zu suchen, zu finden und nicht aufzugeben.“
Alfred Lord Tennyson Ulysses“
”
i
Inhaltsverzeichnis
1
Einleitung
1
2 Theoretische Grundlagen
2.1 Magnetische Wechselwirkungen . . . . . . . . . .
2.1.1 Dipol-Dipol-Wechselwirkung und Streufeld
2.1.2 Austauschwechselwirkung . . . . . . . . .
2.2 Landau-Lifschitz-Gleichung . . . . . . . . . . . .
2.3 Polder-Suszeptibilitäts-Tensor . . . . . . . . . . .
2.4 Spinwellen . . . . . . . . . . . . . . . . . . . . .
2.5 Dispersionsrelation für austauschdominierte Moden
2.6 Dispersionsrelationen dipolarer Moden . . . . . . .
2.6.1 Walker-Gleichung . . . . . . . . . . . . .
2.6.2
Backward“-Volumenmoden . . . . . . . .
”
2.6.3 Oberflächenmoden . . . . . . . . . . . . .
2.6.4 Eigenschaften der Dispersionsrelationen . .
2.6.5 Modifikation der Dispersionsrelationen . .
2.7 Elektro-optischer Effekt . . . . . . . . . . . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
3 Experimentelle Methoden
3.1 Aufbau der Probe . . . . . . . . . . . . . . . . . . . . . . . . . .
3.2 Mikrowellenmesstechnik . . . . . . . . . . . . . . . . . . . . . .
3.2.1 Eingangsnetzwerk . . . . . . . . . . . . . . . . . . . . .
3.2.2 Ausgangsnetzwerk . . . . . . . . . . . . . . . . . . . . .
3.3 Brillouin-Lichtstreuspektroskopie . . . . . . . . . . . . . . . . .
3.3.1 Brillouin-Lichtstreuprozess . . . . . . . . . . . . . . . . .
3.3.2 Experimenteller Aufbau . . . . . . . . . . . . . . . . . .
3.3.3 Tandem-Fabry-Pérot-Interferometer . . . . . . . . . . . .
3.4 Orts- und zeitaufgelöste Brillouin-Lichtstreuspektroskopie . . . .
3.5 Erweiterung zur phasenaufgelöste Brillouin-Lichtstreuspektroskopie
ii
3
3
3
4
5
7
8
9
10
11
12
14
16
18
18
21
21
23
23
24
25
25
26
28
29
30
INHALTSVERZEICHNIS
3.6
Elektro-optischer Modulator . . . . . . . . . . . . . . . . . . . .
iii
32
4 Experimentelle Ergebnisse
35
4.1 Propagation von dipolaren Spinwellen durch ein inhomogenes Feld 35
4.1.1 Ursache der Phasenverschiebung . . . . . . . . . . . . . . 35
4.1.2 Versuchsaufbau . . . . . . . . . . . . . . . . . . . . . . . 37
4.1.3 Propagation von Backward“-Volumenmoden durch eine
”
starke Inhomogenität . . . . . . . . . . . . . . . . . . . . 38
4.1.4 Propagation einer Backward“-Volumenmode durch eine
”
schwache Inhomogenität . . . . . . . . . . . . . . . . . . 44
4.1.5 Strom-induzierte Phasenverschiebung einer Damon-EshbachMode . . . . . . . . . . . . . . . . . . . . . . . . . . . . 49
4.1.6 Spinwellen-Logik-Gatter . . . . . . . . . . . . . . . . . . 51
4.2 Tunneln von Spinwellen durch eine mechanische Lücke . . . . . . 56
4.2.1 Tunneln durch eine Lücke . . . . . . . . . . . . . . . . . 56
4.2.2 Tunneln durch zwei Lücken . . . . . . . . . . . . . . . . 56
4.3 Erste Tests der phasenaufgelösten Brillouin-Lichtstreuspektroskopie 59
4.3.1 Phasenaufgelöste Brillouin-Lichtstreuspektroskopie an cwSpinwellen . . . . . . . . . . . . . . . . . . . . . . . . . 59
4.3.2 Phasenaufgelöste Brillouin-Lichtstreuspektroskopie an Spinwellen-Pulsen . . . . . . . . . . . . . . . . . . . . . . . . 60
4.3.3 Phasenaufgelöste Brillouin-Lichtstreuspektroskopie mit verbessertem Kontrast . . . . . . . . . . . . . . . . . . . . . 61
4.3.4 Phasenaufgelöste Brillouin-Lichtstreuspektroskopie an der
Probe mit mechanischer Lücke . . . . . . . . . . . . . . . 61
5 Zusammenfassung und Ausblick
64
Literaturverzeichnis
66
Kapitel 1
Einleitung
Zur Untersuchung von Spinwellen wurden seit den sechziger Jahren verschiedene
Techniken eingesetzt. Erste Untersuchungen durchgeführt von Eshbach nutzten
die Abstrahlung von Mikrowellen bei der Reflektion der Spinwellen an den Grenzen der verwendeten Probe [1, 2].
Weitere Möglichkeiten zur Beobachtung von Spinwellen sind die Verwendung von Mikrowellenantennen und die Brillouin-Lichtstreuspektroskopie (BLS).
Während die Mikrowellentechnik nur den integralen Nachweis von Spinwellen an
der Position der Antenne ermöglicht, erlaubt die Brillouin-Lichtstreuspektroskopie
Untersuchungen an beliebig wählbaren Punkten der Probe.
Mithilfe dieser Methoden konnte die Propagation von Spinwellen in verschiedenen Materialien untersucht werden. Dabei galt das Interesse insbesondere nichtlinearen Phänomenen, da diese bei Spinwellen deutlich einfacher als zum Beispiel
bei Licht zu erzeugen sind. So konnte zum Beispiel die Ausbildung und Ausbreitung von Solitonen beobachtet werden (z.B. [3]).
Sowohl die detektierte Mikrowelle, als auch das gestreute Licht enthalten die
Phaseninformation der Spinwelle. Durch den Nachweis der Photonen beziehungsweise die Gleichrichtung der gemessenen Mikrowellenamplitude geht diese allerdings verloren.
Um trotzdem Information über die Phase zu erhalten, kann das gemessene
Signal mit einem kohärenten Referenzsignal gleicher Frequenz überlagert werden.
Man erhält ein Interferenzbild, das Information über Amplitude und Phase enthält.
Bei der Verwendung von Mikrowellenantennen zum Nachweis der Spinwellen
konnten mit dieser Methode bereits gute Resultate erzielt werden [4]. Trotzdem
wurden bisher nur wenige Untersuchungen der Phaseneigenschaften von Spinwellen veröffentlicht.
In dieser Arbeit sollen daher neue Methoden zur Bestimmung und Beeinflussung der Phaseneigenschaften von Spinwellen in Yttrium-Eisen-Granat-Wellen1
KAPITEL 1. EINLEITUNG
2
leiterstrukturen vorgestellt und untersucht werden. Dabei werden nur lineare Spinwellen untersucht, um die neuen Techniken zunächst ohne den Einfluss von nichtlinearen Effekten testen zu können.
Nachdem in Kapitel 2 ein kurzer Überblick über die theoretischen Grundlagen
gegeben wird, werden in Kapitel 3 die verwendeten Messtechniken vorgestellt.
Dabei wird auch der Aufbau der phasenaufgelösten Brillouin-Lichtstreuspektroskopie beschrieben.
In Kapitel 4 werden die gewonnenen Resultate vorgestellt. Zunächst wird gezeigt, dass ein lokal geändertes magnetisches Feld zu einer kontrollierten Phasenverschiebung der Spinwelle führt. Basierend auf diesen Effekt wird ein neues
Konzept zum Aufbau von magnetischer Logik vorgestellt und getestet.
Aufbauend auf die Resultate zum Tunneln einer Spinwelle durch ein lokal abgesenktes Feld [5], werden anschließend orts- und zeitaufgelöste BLS-Messungen
des Tunnelns durch eine mechanische Lücke präsentiert. Außerdem werden die
ersten Messung, die mit der phasenaufgelösten Brillouin-Lichtstreuspektroskopie
durchgeführt wurden, gezeigt.
Die Arbeit schließt mit einer Zusammenfassung, in der auch einige weiterführende, geplante Projekte kurz vorgestellt werden.
Kapitel 2
Theoretische Grundlagen
Im Folgenden sollen die notwendigen theoretischen Grundlagen, die zum Verständnis dieser Arbeit notwendig sind, kurz dargestellt werden. Alle Rechnungen werden im Gauß-System durchgeführt. Eine Umrechnungstabelle in das SISystem findet man zum Beispiel in [6], weiterführende Darstellungen zur Spindynamik in [7, 8].
2.1
Magnetische Wechselwirkungen
2.1.1 Dipol-Dipol-Wechselwirkung und Streufeld
Die Wechselwirkungsenergie zwischen zwei Dipolen µ1 und µ2 im Abstand r
beträgt [9]
µ1 · µ2
(µ1 · r)(µ2 · r)
.
(2.1)
E(µ1 , µ2 , r) =
−3
r3
r5
Die Dipol-Dipol-Wechselwirkung ist langreichweitig, daher muss in einem Festkörper über alle Atome summiert werden. Betrachtet man zwei Momente µ = µB
im Abstand von zwei Bohr’schen Radien a0 erhält man für die Wechselwirkungsenergie E ≈ 0,6 meV. Diese Energie entspricht einer thermischen Energie von
etwa 7 K. Vergleicht man diese Temperatur mit der Curie-Temperatur typischer
Ferromagnete (Fe: 1043 K, Ni: 627 K), ist offensichtlich, dass die Dipol-DipolWechselwirkung nicht die Ursache für die ferromagnetische Ordnung sein kann.
Die magnetische Momente im Inneren eines Festkörpers werden in vielen
Fällen (z.B. bei kubischen Kristallstruktur) kompensiert und liefern keinen Beitrag zur Dipolenergie. An der Oberfläche existieren allerdings unkompensierte
Momente, die das sogenannte Streufeld oder Entmagnetisierungsfeld erzeugen.
3
KAPITEL 2. THEORETISCHE GRUNDLAGEN
4
Zur Berechnung dieses Streufeldes verwendet man die magnetostatischen Maxwellgleichungen [9]
∇ × HS = 0
∇ · B = ∇ · (HS + 4πM ) = 0.
(2.2)
(2.3)
Gleichung (2.2) erlaubt die Definition eines Potentials φ mit HS = −∇φ. Einsetzen in die Maxwellgleichung (2.3) liefert
φ = 4π∇ · M = −ρM .
(2.4)
Dieser Ausdruck entspricht der Poisson-Gleichung mit einer magnetischen Ladungsdichte ρM = −4π∇ · M , daher können die aus der Elektrostatik bekannten
Lösungen [9] übernommen werden.
Für einen homogen magnetisierten Ellipsoid erhält man eine lineare Beziehung zwischen Magnetisierung M und Streufeld HS . Diese kann in der Form
↔
HS = −4πN M
(2.5)
↔
geschrieben werden. N ist ein symmetrischer Tensor und heißt Entmagnetisierungstensor. Im Hauptachsensystem des Ellipsoiden kann er diagonalisiert werden. Die Diagonalelemente für einige Körper sind in Tab. 2.1 angegeben.
Nxx
Nyy
Nzz
1
3
1
2
1
3
Zylinder ez
1
3
1
2
0
Film in (x, y)-Ebene
0
0
1
Kugel
Tabelle 2.1: Diagonalelemente des Entmagnetisierungstensors für verschiedene Körper.
2.1.2 Austauschwechselwirkung
Wie in Kapitel 2.1.1 gezeigt wurde, ist die Dipol-Dipol-Wechselwirkung nicht die
Ursache für die ferromagnetische Ordnung. Die Ordnung lässt sich erklären,
wenn man die quantenmechanischen Austauschwechselwirkung berücksichtigt.
Diese wurde erstmals von Heisenberg [10] behandelt, die wesentlichen Überlegungen dazu sind im Folgenden wiedergegeben.
Elektronen sind Fermionen, das heißt die Wellenfunktion eines Mehrelektronensystems muss antisymmetrisch unter Vertauschung zweier Teilchen sein
KAPITEL 2. THEORETISCHE GRUNDLAGEN
5
(Pauli-Prinzip) [11]. Betrachtet man ein Zwei-Elektronen-System, so sind deshalb nur Kombinationen aus einer symmetrischen Spinwellenfunktion (parallele
Spins) mit einer antisymmetrischen Ortswellenfunktion oder umgekehrt möglich.
Diese beiden Möglichkeiten führen zu verschiedenen Aufenthaltswahrscheinlichkeiten für die Elektronen und damit zu verschiedenen Energieeigenwerten.
Die Differenz zwischen diesen Energien nennt man Austauschenergie Eex .
Der Hamilton-Operator für die Austauschwechselwirkung zwischen zwei
Spins kann daher in der Form
Ĥ = −Eex
1
1
Ŝ · Ŝ2 = −2J 2 Ŝ1 · Ŝ2
2 1
h̄
h̄
(2.6)
geschrieben werden. Ŝ1 und Ŝ2 sind die Spinoperatoren. Die Kopplungskonstante
J kann beide Vorzeichen annehmen. Ist sie positiv sind parallele Spins energetisch
günstiger, man spricht von Ferromagnetischer Kopplung“. Im umgekehrten Fall
”
stellen sich die Spins bevorzugt antiparallel, es ergibt sich Antiferromagnetische
”
Kopplung“ [12].
Eine quantenmechanische Rechnung zeigt, dass J durch das Überlappintegral
der Ein-Elektronen-Wellenfunktionen der beteiligten Elektronen dargestellt werden kann [13]. Da nur die Wellenfunktionen von benachbarten Atomen nennenswert überlappen ist die Austauschwechselwirkung kurzreichweitig.
Für einen Festkörper mit n Spins kann der Hamilton-Operator der Austauschwechselwirkung als Näherung durch die Summation über die Zwei-Spin-Wechselwirkung zwischen allen Paaren von Spins beschrieben werden. Ist die Kopplung
für alle Paare gleich, erhält man
(2.7)
Ŝn · Ŝn+m .
Ĥ = −J
m
n
Die Summation über m kann aufgrund der kurzen Reichweite der Austauschwechselwirkung auf die z nächsten Nachbarn beschränkt werden, so dass sich der
Hamilton-Operator in der Form
Ĥ = −J
z δ
Ŝn · Ŝn+δ .
(2.8)
n
darstellen lässt.
2.2
Landau-Lifschitz-Gleichung
Die Landau-Lifschitz-Gleichung ist die Bewegungsgleichung der Magnetisierung
in einem magnetischen Feld. Sie soll im Folgenden phänomenologisch hergeleitet
werden.
KAPITEL 2. THEORETISCHE GRUNDLAGEN
6
Auf ein magnetisches Moment µ in einem Magnetfeld H wirkt ein Drehmoment
T = µ × H.
(2.9)
Ein magnetisches Moment, das nicht parallel zum Feld ausgerichtet ist, präzediert
um die Feldrichtung, bis es sich durch Dämpfungsprozesse parallel zum Feld einstellt.
Das magnetische Moment µ ist mit dem Drehimpuls L durch
L=−
µ
|γ|
(2.10)
verknüpft (z.B. [14, Kapitel 12]). γ ist das gyromagnetische Verhältnis. Mit
Gl. (2.9) erhält man daraus
T=
dL
1 dµ
=−
= µ × H.
|γ| dt
dt
(2.11)
Der Übergang zur Magnetisierung M liefert die Landau-Lifschitz-Gleichung [15]
dM
= − |γ| M × Heff .
dt
(2.12)
Heff ist dabei das effektive Feld, das auf die Magnetisierung wirkt
Heff = H0 + H(t) + Hani + Hex + HS .
(2.13)
H0 ist das konstante äußere Feld. H(t) enthält sowohl das zeitabhängige Feld,
das durch die Präzession des magnetischen Moments verursacht wird, als auch
einen eventuellen zeitabhängigen Anteil des äußeren Feldes. Hani und Hex beschreiben das Anisotropie- und das Austauschfeld, HS das Streufeld (vgl. Kapitel 2.1.1).
Dämpfungsprozesse können durch das Einfügen eines empirischen Zusatzterms berücksichtigt werden. Landau und Lifschitz schlugen dazu eine Erweiterung von Gl. (2.12) der Form
λ |γ|
dM
= − |γ| M × Heff −
M × (M × Heff )
|M |
dt
(2.14)
vor [15]. λ ist ein dimensionsloser Dämpfungsparameter. Dieser Ansatz kann
nur für kleine λ verwendet werden, da die Stärke der Dämpfung mit λ ohne Beschränkung steigt. Dieses Verhalten widerspricht allen Beobachtungen.
Ein von Gilbert [16] vorgeschlagener alternativer Ansatz hat die Form
dM
dM
α
M×
= − |γ| M × Heff −
|M |
dt
dt
(2.15)
KAPITEL 2. THEORETISCHE GRUNDLAGEN
7
und behebt dieses Problem. Im Fall kleiner Dämpfung (α 1, λ 1) ist er
äquivalent zu Gl. (2.14) [16].
Die Dämpfung steht in beiden Fällen senkrecht zur Magnetisierung und ändert
daher die Länge von M nicht, wie durch Multiplikation von Gl. (2.14) und (2.15)
mit M und Berücksichtigung von
M
1d
dM
=
M2
dt
2 dt
gezeigt werden kann.
2.3
Polder-Suszeptibilitäts-Tensor
Die Landau-Lifschitz-Gleichung (2.12) lässt sich im Fall kleiner Auslenkungen
aus der Ruhelage zu einer linearen Beziehung zwischen den dynamischen Anteilen des magnetischen Feldes Heff und der Magnetisierung M umformen. Dazu
wird angenommen, dass sich die dynamischen Anteile als kleine harmonische
Störungen
M = M0 + m(t)
Heff = H0 + h(t),
(2.16)
2 mit
m(t) = me−iωt
|m| |M0 |
h(t) = he−iωt
|h| |H0 |
(2.17)
schreiben lassen. Weiter soll gelten
H0 = H0 ez
M0 = MS ez .
(2.18)
Das entspricht einem magnetisch gesättigten Ein-Domänen-Zustand ohne Anisotropie, also zum Beispiel einem magnetisierten dünnen Film. MS ist die Sättigungsmagnetisierung. Feld und Magnetisierung sind in z-Richtung orientiert.
Für kleine Auslenkungen aus dem Gleichgewicht bleiben die z-Komponenten von
H0 und M0 unverändert, das heißt m und h haben nur Komponenten in x- und
y-Richtung. Einsetzen von Gl. (2.16) in die Landau-Lifschitz-Gleichung ohne
Dämpfung (2.12) ergibt
dm(t)
= −|γ| [M0 × H0 + M0 × h(t) + m(t) × H0 + m(t) × h(t)] .
dt
(2.19)
KAPITEL 2. THEORETISCHE GRUNDLAGEN
8
Der erste Term in der Klammer ergibt null (da H0 M0 ); der letzte Term kann als
Produkt zweier kleiner Größen vernachlässigt werden. Einsetzen von Gl. (2.17)
und (2.18) liefert
(2.20)
iωm = |γ|ez × [MS h − H0 m] .
↔
Bringt man Gl. (2.20) in die Form m = χh, so erhält man


χ −iκ 0
1 
↔
iκ χ 0
χ=
4π
0
0 0
mit
χ=
ωH ωM
ω2H − ω2
(2.21)
ω ωM
ω2H − ω2
(2.22)
ωH = |γ|H0 .
(2.23)
κ=
und
ωM = |γ|4πMS
↔
χ heißt Polder-Suszeptibilitäts-Tensor [8, Kapitel 2.7].
2.4
Spinwellen
Betrachtet man ein magnetisches Moment, das durch eine Störung aus der Ruhelage ausgelenkt wurde, beschreibt die Landau-Lifschitz-Gleichung (2.12) die
Präzession dieses Momentes um die Richtung der Magnetisierung. Das Moment
koppelt dabei durch die Dipol-Dipol- (vgl. Kapitel 2.1.1) und die Austauschwechselwirkung (vgl. Kapitel 2.1.2) an die benachbarten Momente. Die Störung breitet
sich daher als Welle im Festkörper oder genauer im Spinsystem des Festkörpers
aus. Man spricht von Spinwellen oder, in der Sprache der zweiten Quantisierung [17], von Magnonen.
Da das magnetische Moment konstant bleiben muss, haben Spinwellen nur
zwei Freiheitsgrade [18].
Bei der theoretischen Beschreibung von Spinwellen ist zu beachten, dass sich
die beiden Wechselwirkungen sowohl in Stärke als auch in Reichweite deutlich
unterscheiden. Daher muss abhängig von der Wellenlänge λ der betrachteten
Spinwelle nur eine der Wechselwirkungen berücksichtigt werden.
Ist die Wellenlänge klein, so ist die Austauschwechselwirkung zwischen benachbarten Spins groß, da diese stark gegeneinander verkippt sind. Die schwache
dipolare Wechselwirkung kann daher vernachlässigt werden, man spricht von austauschdominierten Moden (vgl. Kapitel 2.5).
KAPITEL 2. THEORETISCHE GRUNDLAGEN
9
Für große Wellenlängen ist die Verkippung zwischen benachbarten Spins sehr
gering, die Austauschwechselwirkung ist schwach und kann gegenüber der dipolaren Wechselwirkung vernachlässigt werden. Man spricht daher auch von dipolaren Moden. Diese werden in Kapitel 2.6 behandelt.
2.5
Dispersionsrelation für austauschdominierte
Moden
Die Spinoperatoren in Gl. (2.8) können durch die Pauli-Spinmatrizen
h̄ 0 1
h̄ 0 −i
h̄ 1 0
x
y
z
Ŝ =
Ŝ =
Ŝ =
2 1 0
2 i 0
2 0 −1
(2.24)
dargestellt werden [11]. Anstelle der Operatoren Ŝx und Ŝy ist es günstiger, die
Spinumklappoperatoren
(2.25)
Ŝ± = Ŝx ± iŜy
zu verwenden. Die Spineigenzustände werden durch
1
0
|↑ =
|↓ =
0
1
(2.26)
dargestellt. Die Wirkung der Operatoren auf diese Zustände ist
Ŝ+ |↑ = 0
Ŝ+ |↓ = |↑
Ŝ− |↑ = |↓
Ŝ− |↓ = 0
(2.27)
und
1
Ŝz |↑ = |↑
2
1
Ŝz |↓ = − |↓.
2
(2.28)
Mit diesen Operatoren lässt sich der Austausch-Hamilton-Operator (2.8) als
z 1
+ −
z z
− +
(2.29)
Ĥ = −J
Ŝn Ŝn+m + Ŝn Ŝn+m + Ŝn Ŝn+m
2
n
δ
darstellen. Die Summation über n berücksichtigt alle Spins, δ berücksichtigt nur
die z nächsten Nachbarn. Der Grundzustand dieses Operators kann zum Beispiel
durch
|↑ j
(2.30)
|0 =
j
KAPITEL 2. THEORETISCHE GRUNDLAGEN
10
beschrieben werden. Ein Zustand, in dem nur einer der Spins umgeklappt ist, wie
zum Beispiel |↓m = Ŝ−
m |0, ist kein Eigenzustand von Gl. (2.29), da der Operator
−
+
Ŝm Ŝm+δ diesen Spin an den Ort m + δ verschieben und damit einen neuen Zustand
erzeugen würde. Bildet man eine Linearkombination aus allen |↓m , wie zum
Beispiel
1 ik·rm
e
|↓m ,
(2.31)
|k = √
N m
erhält man einen Eigenzustand von Gl. (2.29) [19]. Der Zustand |k beschreibt
eine Spinwelle mit Wellenvektor k. Die Energie dieses Zustandes erhält man aus
Ĥ|k = E|k. Sie lässt sich schreiben als
z
z
1 ik·rδ
+ e−ik·rδ
cos (k · rδ ) .
e
= E0 + J z −
E = E0 + J z −
2
δ
δ
(2.32)
Für nicht zu große Wellenvektoren k kann der Ausdruck entwickelt werden. Man
erhält
z
1 E ≈ E0 + J
(k · rδ )2 .
(2.33)
2
δ
Mit E = h̄ω ergibt sich für die Dispersion von austauschdominierten Spinwellen
ω ∼ k2 .
2.6
(2.34)
Dispersionsrelationen dipolarer Moden
Zur Berechnung der Dispersionsrelationen dipolarer Moden wird im wesentlichen
der Ansatz von Damon und Eshbach [20,21] verwendet. Es wird allerdings darauf
verzichtet, die Dispersion für beliebige Winkel zwischen der Magnetisierung M0
und dem Wellenvektor k zu berechnen. Stattdessen werden nur die experimentell
realisierten Fälle M0 parallel zu k (Kapitel 2.6.2) und M0 senkrecht zu k (Kapitel
2.6.3) betrachtet (vgl. z.B. [8]).
Außerdem wird hier nur die räumliche Verteilung des Feldes und die Magnetisierung betrachtet. Die Zeitabhängigkeit wurde bereits bei der Herleitung des
Polder-Suszeptibilitäts-Tensor berücksichtigt (vgl. Gl. (2.16)).
Ausgangspunkt für die Berechnung der Dispersionsrelationen der dipolaren
Moden sind die magnetostatischen Maxwellgleichungen ohne Ströme [9]
∇×H = 0
∇ · B = 0.
(2.35)
KAPITEL 2. THEORETISCHE GRUNDLAGEN
11
Diese sind gültig, wenn alle Änderungen quasistatisch, das heißt langsam gegenüber der Lichtgeschwindigkeit ablaufen. Dieser Fall ist bei allen hier betrachteten Systemen gegeben.
Für die Beziehung zwischen B und H gilt
B = H+4πM .
(2.36)
2.6.1 Walker-Gleichung
Setzt man Gl. (2.17) in die magnetostatischen Maxwell-Gleichungen (2.35) ein,
erhält man unter Verwendung von Gl. (2.36)
∇×h = 0
∇ · (h + 4πm) = 0.
(2.37)
(2.38)
Gleichung (2.37) erlaubt wegen ∇ × (∇Ψ) = 0 die Definition eines skalaren Potentials Ψ, für das gilt
h = −∇Ψ.
(2.39)
Weiter gilt
↔
m = χh,
(2.40)
↔
mit dem Polder-Suszeptibilitäts-Tensor χ (2.21). Einsetzen von Gl. (2.39) und
(2.40) in die Maxwellgleichung (2.38) ergibt
↔
∇ · 1 + 4πχ · ∇Ψ = 0.
(2.41)
Auflösen dieses Ausdrucks liefert die sogenannte Walker-Gleichung [22]
2
∂ Ψ ∂2 Ψ
∂2 Ψ
(1 + χ)
+
+
= 0,
(2.42)
∂x2
∂y2
∂z2
mit
χ=
ωH ωM
,
ω2H − ω2
die der Ortsanteil des Potentials Ψ erfüllen muss.
Für χ = −1 liefert die Walker-Gleichung (2.42) Lösungen, die propagierende Spinwellen beschreiben. Diese Lösungen werden in den folgenden Kapiteln
behandelt.
Ist χ = −1 wird die Walker-Gleichung (2.42) durch ein beliebiges, von z unabhängiges Potential Ψ(x, y) gelöst. Man erhält
ω2 = ωH (ωH + ωM ).
(2.43)
KAPITEL 2. THEORETISCHE GRUNDLAGEN
12
Dieser Ausdruck entspricht der sogenannten Herring-Kittel Formel für dünne Filme [23, 24] und beschreibt die ferromagnetische Resonanzabsorption, das heißt
eine homogene Anregung des gesamten Spinsystems. Eine quantenmechanische
Herleitung von Gl. (2.43) findet man in [25].
2.6.2
Backward“-Volumenmoden
”
Mit Hilfe der Walker-Gleichung (2.42) soll nun die Dispersionsrelation einer dipolaren Spinwelle in einem unendlich ausgedehnten, tangential magnetisierten
Film der Dicke d in der y-z-Ebene berechnet werden. In diesem Fall existiert kein
statisches Streufeld HS , und das statische Feld im Inneren des Films entspricht
dem äußeren Feld H0 = H0 ez . Zunächst soll dabei die Propagation parallel zur
Magnetisierung betrachtet werden (vgl. Abb. 2.1).
H0
mx ex + my ey
MS ez
y
z
x
− d2
0
d
2
2
k
1
3
Abbildung 2.1: Koordinatensystem für die Berechnung der Dispersionsrelation für
Backward“-Volumenmoden. Die Magnetisierung M0 und das Feld H0 sind in der Film”
ebene in z-Richtung orientiert. Die Welle propagiert ebenfalls in z-Richtung.
Innerhalb des Films (−d/2 ≤ x ≤ d/2, Gebiet 1 in Abb. 2.1) gilt die WalkerGleichung (2.42), außerhalb (x < −d/2, x > d/2, Gebiete 2 und 3 in Abb. 2.1) gilt
die Laplace-Gleichung Ψ2,3 = 0, da dort keine Magnetisierung vorhanden ist.
Als Ansatz für das Potential Ψ wird eine ebene Welle in z-Richtung ohne yAbhängigkeit
(2.44)
Ψ(x, z) = X(x)eikz
KAPITEL 2. THEORETISCHE GRUNDLAGEN
13
gewählt. Einsetzen in die Walker- bzw. Laplace-Gleichung liefert
X1 (x) = A1 cos (qx) + B1 sin (qx)
|x| <
d
2
X2 (x) = A2 ekx + B2 e−kx
x<−
X3 (x) = B3 e−kx + A3 ekx
x>
d
2
(2.45)
d
2
(2.46)
mit
k
q= .
−(1 + χ)
(2.47)
Die jeweils zweiten Terme in Gl. (2.46) sind physikalisch nicht sinnvoll, da sie
nach außen exponentiell ansteigen und werden daher nicht weiter verwendet. Anhand von Gl. (2.47) sieht man, dass propagierende Spinwellen in dieser Geometrie
für 1 + χ < 0, das heißt im Frequenzbereich
(2.48)
ωH < ω < ωH (ωH + ωM )
existieren.
An den Rändern des Films müssen die Tangentialkomponente von h und die
↔
Normalkomponente von b = h + 4πm = h(1 + 4πχ) stetig sein, das heißt es
gelten die Randbedingungen
d
d
hy,z,1 x = −
= hy,z,2 x = −
2
2
d
d
= hy,z,3 x =
(2.49)
hy,z,1 x =
2
2
d
d
= bx,2 x = −
bx,1 x = −
2
2
d
d
bx,1 x =
= bx,3 x =
.
(2.50)
2
2
Aus Gl. (2.49) folgt
d
d
X1 x = −
= X2 x = −
2
2
d
d
= X3 x =
.
X1 x =
2
2
(2.51)
KAPITEL 2. THEORETISCHE GRUNDLAGEN
14
Gleichung (2.50) liefert
∂X1 ∂X2 −(1 + χ)
=−
∂x x=− d
∂x x=− d
2
2
∂X1 ∂X3 −(1 + χ)
=−
.
∂x x= d
∂x x= d
2
(2.52)
2
Einsetzen von Gl. (2.46) und (2.45) in Gl. (2.51) und (2.52) liefert das Gleichungssystem
dk
dq
dq
A1 cos
− B1 sin
= A 2 e− 2
2
2
dk
dq
dq
+ B1 sin
= B 3 e− 2
A1 cos
2
2
dk
dq
dq
+ B1 q cos
= A2 ke− 2
A1 q sin
2
2
dk
dq
dq
A1 q sin
(2.53)
− B1 q cos
= B3 ke− 2 .
2
2
Die Lösung dieses Systems liefert die Dispersionsrelation
2
−(1 + χ) arctan
−(1 + χ)
(2.54)
k=
d
mit
ωH ωM
χ= 2
ωH − ω2
für Spinwellen, die parallel zum anliegenden Feld propagieren [21]. Abbildung 2.3
zeigt, dass ω(k) streng monoton fallend ist. Daraus ergibt sich, dass die Gruppengeschwindigkeit vg = ∂ω/∂k negativ ist. Gruppengeschwindigkeit vg und
Wellenvektor k sind also antiparallel. Daher spricht man auch von Backward“”
Volumenmoden (Backward Volume Magnetostatic Spin Waves, BVMSW). Eine
Erklärung dieses Verhaltens wird in Kapitel 2.6.4 gegeben.
Eine von Kalinikos und Slavin hergeleiteten Näherung kann im Gegensatz zu
Gl. (2.54) nach ω aufgelöst werden und liefert gute Resultate für kd 1 [26].
Man erhält
1 − e−kd
2
.
(2.55)
ω = ωH ωH + ωM
kd
2.6.3 Oberflächenmoden
Die Berechnung der Dispersionsrelation bei Propagation senkrecht zur Magnetisierung (d. h. in y-Richtung, vgl. Abb. 2.2), erfolgt analog zu Kapitel 2.6.2.
KAPITEL 2. THEORETISCHE GRUNDLAGEN
15
H0
y
z
x
− d2
0
d
2
2
k
1
3
Abbildung 2.2: Koordinatensystem für die Berechnung der Dispersionsrelation für Oberflächenmoden. Die Magnetisierung M0 und das Feld H0 liegen in der Filmebene in
z-Richtung. Die Welle propagiert senkrecht zur Magnetisierung in y-Richtung.
Als Ansatz für das Potential Ψ wird eine ebene Welle in y-Richtung
Ψ(x, y) = X(x)eiky
(2.56)
gewählt. Innerhalb des Films muss das Potential die Walker-Gleichung (2.42)
erfüllen. Für X1 ergibt sich die Gleichung
∂X1
2
(1 + χ)
(2.57)
− k X = 0.
∂x
Für χ = −1 wird diese durch
X1 = A1 ekx + B1 e−kx
(2.58)
gelöst. Die Spinwelle ist im Gegensatz zur BVMSW an der Filmoberfläche lokalisiert, daher spricht man auch von Oberflächenmoden (Magnetostatic Surface
Spin Waves, MSSW) oder Damon-Eshbach-Moden [21].
Außerhalb des Films muss die Laplace-Gleichung erfüllt werden. Da diese
unabhängig von der Richtung von k und H0 ist, erhält man wie bei den Back”
ward“-Volumenmoden die Lösungen (2.46).
Die Randbedingungen (2.49) und (2.50) müssen auch in dieser Geometrie erfüllt werden. Die Randbedingungen für h (2.49) nehmen dabei dieselbe Form
an wie im Fall von BVMSW, so dass Gl. (2.51) erfüllt werden muss. Bei den
Randbedingungen für b ist allerdings zu beachten, dass hier Ψ auch eine Funktion
↔
von y ist, h also auch eine y-Komponente hat, die über χ einen Einfluss auf bx
KAPITEL 2. THEORETISCHE GRUNDLAGEN
16
hat. Gleichung (2.50) liefert daher
∂X1 d
(1 + χ)
+ κkX1 x = −
=
∂x x=− d
2
2
d
∂X1 =
(1 + χ)
+ κkX1 x =
∂x d
2
x= 2
∂X2 ∂x x=− d
2
∂X3 .
∂x d
(2.59)
x= 2
Einsetzen von Gl. (2.46) und (2.58) in die Randbedingungen (2.51) und (2.59) liefert das Gleichungssystem
A1 e−k 2 + B1 ek 2
d
= A2 e−k 2
d
d
A1 ek 2 + B1 e−k 2
d
= B3 e−k 2
d
d
−(1 + χ + κ)A1 e−k 2 + (1 + χ + κ)B1 ek 2 = A2 e−k 2
d
d
d
−(1 + χ + κ)A1 ek 2 + (1 + χ + κ)B1 e−k 2 = B3 e−k 2 .
d
d
Die Lösung dieses Systems liefert die Dispersionsrelation
ω2M 2
−2kd
1−e
.
ω = ωH (ωH + ωM ) +
4
d
(2.60)
(2.61)
MSSW existieren also im Frequenzbereich
1
ωH (ωH + ωM ) < ω < ωH + ωM .
2
(2.62)
Abbildung 2.3 zeigt die Dispersionsrelation für MSSW zusammen mit der
für BVMSW. Die Dispersionsrelation (2.61) ist monoton steigend, dass heißt die
Gruppengeschwindigkeit ist positiv.
Werden aus dem Gleichungssystem (2.60) die Koeffizienten A1 und B1 bestimmt, erkennt man, dass Gl. (2.58) und damit das Potential im Inneren des Filmes, abhängig vom Vorzeichnen von k nur an einer der Filmoberflächen nennenswert von null verschieden ist. Oberflächenmoden haben also einen definierten
Umlaufsinn.
2.6.4 Eigenschaften der Dispersionsrelationen
Wie schon erwähnt wurde, ist die Dispersionsrelation für BVMSW monoton fallend, die für MSSW monoton steigend. Die Ursache dieses Unterschieds wird in
Abb. 2.4 verdeutlicht.
Betrachtet man die dynamische Komponenten der Magnetisierung, so existiert
in beiden Fällen eine Komponente, die in der Ebenen liegt (my ) und eine Komponente, die senkrecht zur Ebene steht (mx ). Letztere bildet ein Streufeld aus. Die
KAPITEL 2. THEORETISCHE GRUNDLAGEN
17
7,4
ωH (ωH + ωM )
7,2
Frequenz [GHz]
7,0
MSSW
6,8
6,6
6,4
6,2
6,0
5,8
5,6
BVMSW
5,4
5,2
0
5000
10000
15000
20000
Wellenvektor [cm−1 ]
25000
Abbildung 2.3: Dispersionsrelation für dipolare Spinwellen in dünnen YIG-Filmen mit
H0 = 1800 Oe, d = 5 µm, 4πMS = 1750 G, γ = 2π · 2,82 · 106 rad/s
Oe .
x
z
y
x
z
y
HS
HS
(a) BVMSW
(b) MSSW
Abbildung 2.4: Ursache des unterschiedlichen Verhaltens der Dispersionsrelationen.
In den Kreisen ist die dynamische Komponente der Magnetisierung dargestellt [27].
(a) BVMSW, (b) MSSW.
KAPITEL 2. THEORETISCHE GRUNDLAGEN
18
dazu nötige Energie wird reduziert, wenn die Wellenlänge abnimmt, da dann die
antiparallelen mx -Komponenten enger zusammen liegen.
Für BVMSW ist die Komponente in der Ebene senkrecht zu k, das heißt die
my -Komponenten von direkt benachbarten Spins zeigen in dieselbe Richtung, daher wird kein weiteres Feld ausgebildet. Die Energie und damit die Frequenz
nimmt mit kleineren Wellenlängen ab. Die Dispersionsrelation ω(k) ist monoton
fallend.
Bei MSSW führt eine Abnahme der Wellenlänge zu einer Verringerung des
Abstandes zwischen entgegengesetzten my Komponenten der dynamischen Magnetisierung. Die daraus resultierende Erhöhung der Dipolenergie ist größer als die
Energieabsenkung durch die Reduzierung des Streufeldes. Die Dispersionsrelation ist daher monoton steigend.
2.6.5 Modifikation der Dispersionsrelationen
Betrachtet man die Grenzfrequenzen für BVMSW (2.48) und MSSW (2.62), so
fällt auf, dass eine Änderung des magnetischen Feldes H0 zu einer Verschiebung
dieser Grenzen führt. Der Verlauf der Dispersionsrelationen bleibt dabei im wesentlichen unverändert (vgl. Abb. 2.5). Eine Änderung von H0 führt also zu einer
Verschiebung der Kurve entlang der Frequenzachse.
Für eine Spinwelle der Frequenz ω führt eine Änderung des Feldes daher zu
einer Änderung des Wellenvektors k und damit der Wellenlänge λ = 2π/k. Eine lokale Änderung des Feldes wird in Kapitel 4.1 ausgenutzt, um die Phase der
Spinwelle zu beeinflussen.
2.7
Elektro-optischer Effekt
Zum Aufbau der phasenaufgelösten Brillouin-Lichtstreuspektroskopie (vgl. Kapitel 3.5) muss ein Teil des eingestrahlten Lichts frequenzverschoben werden. Dazu
wird der sogenannte elektro-optische Effekt verwendet. Darunter versteht man
die Änderung des Brechungsindexes einiger Kristalle durch ein angelegtes elektrisches Feld [28, Kapitel 9]. Diese Änderung wird für Licht, das parallel zu einer
der optischen Achsen des Kristalls polarisiert ist, durch
∆n =
n30
rE
2
(2.63)
beschrieben. E ist das angelegte elektrische Feld, n0 ist der Brechungsindex
des Kristalls ohne elektrisches Feld und r ist das wirksame Element des elektrooptischen Tensors (siehe z.B. [28, Kapitel 9]). Propagiert Licht der Frequenz ω
KAPITEL 2. THEORETISCHE GRUNDLAGEN
19
7,8
7,6
7,4
Frequenz [GHz]
7,2
7,0
1750 Oe
1800 Oe
1850 Oe
6,8
6,6
6,4
6,2
6,0
5,8
5,6
5,4
5,2
5,0
0
5000
10000
15000
Wellenvektor [cm−1 ]
20000
25000
Abbildung 2.5: Verschiebung der Dispersionsrelationen von dipolaren Spinwellen durch
Änderung des magnetischen Feldes H0
.
entlang der y-Achse durch einen Kristall der Länge l erhält es durch das elektrische Feld eine zusätzliche Phasenverschiebung
ωn3 r
ωl
∆n = − 0 lE.
(2.64)
c
2c
c ist die Vakuumlichtgeschwindigkeit.
Im Folgenden wird die elektrische Feldkomponente e des einfallenden Lichts
betrachtet. An der Vorderseite des Kristalls (y = 0) kann diese als
∆ϕ = −
ein = A exp (iωt)
(2.65)
dargestellt werden. Außerdem soll ein elektrisches Wechselfeld
E = Em sin (ωmt)
(2.66)
am Kristall anliegen.
Nach der Propagation durch den Kristall hat die elektrische Feldkomponente
e bei y = l die Form
n30
ω
eout = A exp i ωt −
(2.67)
n0 + rEm sin (ωmt) l .
c
2
KAPITEL 2. THEORETISCHE GRUNDLAGEN
20
Der konstante Phasenterm n0 lω/c ist ohne Bedeutung und kann daher weggelassen werden. Man erhält
eout = A exp [i (ωt + δ sin (ωmt))]
(2.68)
mit
ωn30 rEm l
δ=−
.
2c
Unter Verwendung der Bessel-Funktionen Jn [29] und der Relation
∞
exp (iδ sin (ωmt)) =
Jn (δ) exp (inωmt)
(2.69)
(2.70)
n=−∞
(aus [30]) kann man Gl. (2.68) zu
eout = A
∞
Jn (δ)ei(ω+nωm )t
(2.71)
n=−∞
umformen. Man erkennt, dass das eingestrahlte, monochromatische Licht nach
der Propagation durch den Kristall Seitenbänder bei den Frequenzen ω ± nωm
enthält.
Kapitel 3
Experimentelle Methoden
Im Folgenden werden die experimentellen Techniken für die im Rahmen dieser
Arbeit durchgeführten Untersuchungen vorgestellt. Dazu gehören die BrillouinLichtstreuspektroskopie (BLS, Kapitel 3.3), sowie die Erweiterungen zur ortsund zeitaufgelösten BLS (Kapitel 3.4). Erstmalig verwendet wurde die phasenaufgelöste Brillouin-Lichtstreuspektroskopie (Kapitel 3.5).
3.1
Aufbau der Probe
Die untersuchten Spinwellen wurden in dünnen Filmen aus Yttrium-Eisen-Granat
Y3 Fe5 O12 (Yttrium-Iron-Garnet, YIG) angeregt. Dieser wurde durch Flüssigphasenepitaxie auf ein Substrat aus Gallium-Gadolinium-Granat (GGG) gewachsen1 . Beide Materialien sind transparent.
Die Proben wurden auf einem Substrat aus Duroid oder Aluminiumoxid befestigt (vgl. Abb. 3.1). Auf diesem befinden sich durch Ätzen erzeugte Leiterbahnen
aus Kupfer, die als Ein- und Ausgangsantennen dienen. Ihr Abstand beträgt 8 mm
Die Rückseite des Substrats ist vollständig metallisiert und dient als Masse. Beide Antennen sind auf einer Seite mit der Masse verbunden. Zwischen ihnen ist
ein Fenster in das Substrat geschnitten, damit der Laserstrahl des BLS-Aufbaus
(vgl. Kapitel 3.3) die Probe erreichen kann. Ein Schema des Probenaufbaus ist in
Abb. 3.1 gezeigt.
In Tabelle 3.1 sind die wichtigsten Eigenschaften der hier verwendeten YIGFilme zusammengefasst. Die geringe Dämpfung erlaubt die Beobachtung von
propagierenden Spinwellen über mehrere Millimeter.
1 Die
hier verwendeten Proben wurden von Scientific Research Company ”Carat”, R&D Insti-
tute of Materials, Division of Crystal Growth and Technology, Lviv, Ukraine hergestellt.
21
KAPITEL 3. EXPERIMENTELLE METHODEN
22
Eingangs- und
Ausgangsantenne
Substrat
YIG
GGG
0,5 mm
6 − 7 µm
Masse
Fenster
Abbildung 3.1: Aufbau der Probe. Die Spinwellen propagieren im YIG-Film. Die Einund Ausgangsantenne dienen zur Umwandlung von Mikrowellen in Spinwellen und umgekehrt.
Sättigungsmagnetisierung MS
1750 G
gyromagnetisches Verhältnis γ
2π · 2,82 · 106 rad/s
Oe
FMR-Linienbreite
0,5 Oe
Gilbert-Dämpfungsparameter α
0.00056
Tabelle 3.1: Eigenschaften der verwendeten YIG-Filme.
Zur Anregung von Spinwellen werden Mikrowellen verwendet. Diese bilden
um die Eingangsantenne ein magnetisches Wechselfeld aus, das das Spinsystem
des YIG-Films anregt und so zur Ausbildung von Spinwellen führt [31]. An der
Ausgangsantenne findet der umgekehrte Prozess statt. Die resultierenden Mikrowellen könne detektiert werden (vgl. Kapitel 3.2.2).
Abbildung 3.2 zeigt die Transmissionscharakteristik eines YIG-Films. Dargestellt ist die Transmission in dB für verschiedene Frequenzen. Die Spinwellen
propagierten
parallel zum angelegten Feld H0 = 1833 Oe. Die obere Grenzfre
quenz ωH (ωH + ωM ) für BVMSW ist deutlich bei etwa 7,2 GHz zu erkennen.
Für kleinere Frequenzen, das heißt im Fall von BVMSW kleinere Wellenlängen
der angeregten Spinwellen (vgl. Abb. 2.3), nimmt die Transmission ab. Ursache hierfür ist zum einen, dass die Effektivität der Spinwellenanregung durch
Mikrowellen für kurzwellige Spinwellen abnimmt. Außerdem nimmt die Gruppengeschwindigkeit mit kleiner werdender Frequenz ab, das heißt die räumliche
Dämpfung nimmt zu.
KAPITEL 3. EXPERIMENTELLE METHODEN
23
-20
Transmission [dB]
-25
-30
-35
-40
-45
-50
-55
-60
6,9
7,0
7,1
7,2
7,3
Frequenz [GHz]
Abbildung 3.2: Transmissionscharakteristik eines YIG-Filmes für BVMSW mit
H0 = 1833 Oe.
3.2
Mikrowellenmesstechnik
Die hier untersuchten Spinwellen werden wie in Kapitel 3.1 beschrieben durch
Mikrowellensignale erzeugt und vor ihrem Nachweis wieder in Mikrowellen umgewandelt. Da für die Messungen fast immer gepulste Spinwellen verwendet werden, ist es nötig, aus dem cw-Signal der Mikrowellenquelle kurze, scharf begrenzte Pulse zu erzeugen. Außerdem müssen die Signale vor ihrem Nachweis verstärkt
werden. Daher werden im Folgenden die dazu nötigen Schaltungen beschrieben.
Ein Überblick über die verwendete Mikrowellentechnik wird zum Beispiel
in [32, 33] gegeben.
3.2.1 Eingangsnetzwerk
Abbildung 3.3 zeigt den Schaltplan des Eingangsnetzwerks. Die verwendete Mikrowellenquelle liefert ein kontinuierliches Ausgangssignal einstellbarer Leistung
und Frequenz. Ein Leistungsteiler stellt ein Referenzsignal zur Verfügung, das
zum Betrieb der phasenaufgelösten Brillouin-Lichtstreuspektroskopie (vgl. Kapitel 3.5) und zur Messung der Phase in Kapitel 4.1 benötigt wird. Zur Erzeugung
KAPITEL 3. EXPERIMENTELLE METHODEN
Referenzsignal
Mikrowellenquelle
Leistungs- Ferritisolator
teiler
24
Abschlusswiderstand
schneller Verstärker Y-Zirkulator
Schalter
zur
Probe
Abschwächer
Pulsgenerator
Abbildung 3.3: Schaltplan des Eingangsnetzwerks des Mikrowellenaufbaus.
von Pulsen wird ein schneller Schalter verwendet. Dabei ist besonders wichtig, dass dieser kurze Anstiegs- und Abfallzeiten hat, damit möglichst Pulse mit
Rechteckprofil erzeugt werden. Der Schalter wird von einem Pulsgenerator angesteuert, der auch zur Synchronisation mit dem Oszilloskop (Kapitel 3.2.2) oder
der orts- und zeitaufgelösten Brillouin-Lichtstreuspektroskopie (Kapitel 3.4) verwendet wird. Da die Mikrowellen am geöffneten Schalter reflektiert werden, wird
die Quelle durch einen Ferritisolator geschützt. Die resultierenden Mikrowellenpulse werden anschließend verstärkt. Ein Y-Zirkulator leitet die von der Probe
reflektierten Mikrowellen zu einem Abschlusswiderstand, um den Verstärker zu
schützen. Vor der Probe erlaubt ein einstellbarer Abschwächer die Kontrolle der
Spinwellenintensität. Damit kann sichergestellt werden, dass nur lineare Spinwellen angeregt werden.
3.2.2 Ausgangsnetzwerk
Das Ausgangsnetzwerk ist in Abb. 3.4 dargestellt.
von der
Probe
Detektor
Oszilloskop
Abschwächer Verstärker
Abbildung 3.4: Schaltplan des Ausgangsnetzwerks des Mikrowellenaufbaus.
Die von der Probe kommenden Mikrowellen sind zu schwach, um direkt erfasst zu werden, und werden daher verstärkt. Ein einstellbarer Abschwächer erlaubt eine Anpassung der Intensität. Der Mikrowellendetektor wandelt das Signal
in eine Spannung um, die am Oszilloskop dargestellt wird. Dabei muss beachtet
werden, dass die Beziehung zwischen nachgewiesener Mikrowellenleistung und
KAPITEL 3. EXPERIMENTELLE METHODEN
25
Ausgangsspannung nicht linear ist und das gemessene Signal daher umgerechnet
werden muss.
3.3
Brillouin-Lichtstreuspektroskopie
Der Nachweis von Spinwellen durch eine Mikrowellenantenne hat den Nachteil,
dass die Wellen nur an einer Position und dort auch nur integral über die gesamte
Länge der Antenne registriert werden können. Die hier vorgestellte BrillouinLichtstreuspektroskopie (BLS) erlaubt den Nachweis von Spinwellen [34] (und
Phononen [35]) in einem beliebigen Punkt, dessen Fläche nur durch die Fokusgröße des Lasers begrenzt wird.
3.3.1 Brillouin-Lichtstreuprozess
Im Bild der zweiten Quantisierung (vgl. z.B. [17]) lässt sich die Brillouin-Lichtstreuung als Wechselwirkung eines einfallenden Photons mit einem Magnon verstehen (vgl. Abb. 3.5)
Gestreutes Photon
ωL ± ω, k⊥ ± k
ωL
ωL − ω
ωL + ω
Spinwelle
ω, k
Einfallendes Photon
ωL , k⊥
Abbildung 3.5: Prinzip der Brillouin-Lichtstreuung. Ein Photon wird unter Erzeugung
oder Vernichtung eines Magnons gestreut. Dadurch verschiebt sich die Frequenz des
eingestrahlten Photons um die Magnonenfrequenz.
Wird bei der Streuung ein Magnon der Frequenz ω vernichtet, muss sich aufgrund der Energieerhaltung die Frequenz des Photons ωL erhöhen. Wird ein Magnon erzeugt, wird die Frequenz des Photons vermindert. Man erhält für die Frequenz des gestreuten Photons
ωL = ωL ± ω.
(3.1)
KAPITEL 3. EXPERIMENTELLE METHODEN
26
Dieser Zusammenhang folgt direkt aus der Energieerhaltung, wie man durch Multiplikation von Gl. (3.1) mit h̄ sieht. Wird die Frequenz abgesenkt, spricht man
von einem Stokes-Prozess, wird sie erhöht von einem Anti-Stokes-Prozess. Bei
Zimmertemperatur sind beide im Allgemeinen gleich wahrscheinlich. Eine wichtige Ausnahme ist die Streuung an Oberflächenmoden (vgl. Kapitel 2.6.3). Aufgrund des definierten Umlaufsinnes dieser Moden haben Stokes- und Anti-StokesProzesse unterschiedliche Wahrscheinlichkeiten [36].
Klassisch kann die Brillouin-Lichtstreuung durch eine Veränderung der Dielektrizitätskonstante ε beschrieben werden. Eine propagierende Spinwelle tritt
durch die Spin-Bahn-Kopplung mit dem Elektronensystem des Festkörpers in
Wechselwirkung und führt so zu einer periodischen Fluktuation von ε [37, 38].
Diese beeinflusst das einfallende Licht, so dass nach der Streuung Komponenten
mit den Frequenzen ωL ± ω entstanden sind.
Bei der Streuung wird die Polarisationsebene des inelastisch gestreuten Lichts
um π/2 gedreht.
3.3.2 Experimenteller Aufbau
Der Aufbau der hier verwendeten BLS-Anlage ist in Abb. 3.6 gezeigt. Als Lichtquelle wird ein diodengepumpter, frequenzverdoppelter Nd:YVO4 Laser mit der
Wellenlänge λ = 532 nm verwendet. Ein kleiner Teil des Laserstrahls (etwa 2%)
werden mit einem Strahlteiler abgeteilt und dient als Referenzstrahl zur Stabilisierung des Interferometers. Die verbleibenden 98% werden auf die Probe fokussiert.
Der Strahl durchdringt die Probe und wird inelastisch an den Spinwellen gestreut
(vgl. Kapitel 3.3.1), man spricht von Forward-Scattering“ 2 . Eine zweite Linse
”
sammelt das gestreute Licht.
Ein Polarisationsfilter, der senkrecht zur ursprünglichen Polarisationsrichtung
steht, filtert das elastisch gestreute Licht und den Phononenuntergrund aus, da
die inelastische Streuung an Phononen die Polarisationsrichtung nicht beeinflusst.
Ein räumlicher Filter, der aus zwei Linsen und einer Lochblende besteht, unterdrückt das Hintergrundrauschen, das zum Beispiel durch die Raumbeleuchtung
verursacht wird. Ein Shutter-System führt Referenzstrahl und Messstrahl wieder
zusammen. Zur Frequenzselektion wird ein Tandem-Fabry-Pérot-Interferometer
(vgl. Kapitel 3.3.3) verwendet. Die Ansteuerung der Shutter stellt sicher, dass im
Wellenlängenbereich des Lasers der Referenzstrahl und im Bereich des inelastisch
gestreuten Lichts der Messstrahl verwendet wird. Dadurch ist der Photodetektor
vor der hohen Intensität des elastisch gestreuten Lichts geschützt.
2 Bei
nicht transparenten Proben kann auch das rückwärts gestreute Licht verwendet werden
( Backward-Scattering“).
”
Abbildung 3.6: Aufbau der Brillouin-Lichtstreuspektroskopie. Die einzelnen Komponenten werden im Text näher erklärt (siehe Kapitel 3.2, 3.3.2, 3.3.3 und 3.4).
KAPITEL 3. EXPERIMENTELLE METHODEN
27
KAPITEL 3. EXPERIMENTELLE METHODEN
28
Das Licht, das vom Interferometer durchgelassen wird, passiert einen weiteren
räumlichen Filter und wird von einem Photodetektor (in dem hier verwendeten
Aufbau eine Avalanche-Photodiode [39]) registriert. Die Datenaufnahme erfolgt
mit einem Computer.
3.3.3 Tandem-Fabry-Pérot-Interferometer
Verwendet man ein Fabry-Pérot-Interferometer (Etalon) [40] zur Frequenzselektion, ist keine eindeutige Zuordnung zwischen Plattenabstand und durchgelassener
Wellenlänge möglich. Haben die beiden Etalon-Spiegel den Abstand d, wird Licht
transmittiert, wenn die Wellenlänge die Bedingung
λ
n =d
(3.2)
2
erfüllt. Da n eine beliebige natürliche Zahl sein kann, wird diese Bedingung von
vielen Wellenlängen erfüllt. Das von J. R. Sandercock entwickelte Tandem-FabryPérot-Interferometer löst dieses Problem durch die Verwendung eines zweiten
Etalons [41–43].
Das Prinzip ist in Abb. 3.7 dargestellt. Die beiden Etalons sind in einem Winkel θ zueinander angebracht und bestehen aus zwei parallelen, hochreflektierenden Spiegeln. Ein System aus Umlenkspiegeln und Prismen sorgt dafür, dass
beide zur Kontrastverbesserung mehrfach durchlaufen werden (vgl. Abb. 3.6). Jeweils einer der Spiegel jedes Etalons ist auf einer gemeinsamen, beweglichen
Bühne befestigt, so dass die Spiegelabstände simultan geändert werden können.
Eine Änderung des Spiegelabstandes von FP1 um δL führt zu einer Abstandsänderung um δL · cos (θ) in FP2.
Sind beide Etalons in Resonanz, das heißt transmittieren sie Licht der Wellenlänge λ, so führt eine Abstandsänderung von δL = λ/2 in FP1 zum Erreichen
der nächsten Transmissionsordnung. FP2 ist dann allerdings nicht mehr in Resonanz, so dass das Licht das Etalon nicht passieren kann. Die Tandem-Anordnung
erlaubt also eine eindeutige Zuordnung zwischen der Abstandsänderung δL und
der durchgelassenen Wellenlänge.
Die Verschiebung der Scan-Bühne erfolgt durch einen Piezokristall. Wird
die anliegende Spannung geändert, ändert sich der Spiegelabstand und damit die
durchgelassene Wellenlänge.
Während der gesamten Dauer der Messung (einige Stunden) müssen die Spiegel der Etalons exakt parallel bleiben. Diese Stabilisierung wird durch ein Computerprogramm gesteuert, das auch die Datenerfassung übernimmt [44]. Zur weiteren Erhöhung der Stabilität dient eine aktive Vibrationsdämpfung, außerdem ist
das Interferometer durch den Einbau in eine geschlossene Box weitestgehend von
Temperaturänderungen und Luftbewegungen isoliert.
KAPITEL 3. EXPERIMENTELLE METHODEN
29
δL · cos (θ)
FP2
ω
ω
ω
ω
FP2
Scan-Richtung
θ
Transmission
Umlenkspiegel
FP1
TFP
FP1
δL
Scan-Bühne
Tandem-Fabry-PérotInterferometer
Spiegelabstand
(a) Aufbau
(b) Funktion
Abbildung 3.7: (a) Aufbau des Tandem-Fabry-Pérot-Interferometers. (b) Funktion des
Tandem-Fabry-Pérot-Interferometers [27].
3.4
Orts- und zeitaufgelöste Brillouin-Lichtstreuspektroskopie
Zur Bestimmung der räumlichen Verteilung der Spinwellenintensität kann die
Probe mit Schrittmotoren in y- und z-Richtung bewegt werden. Die erreichbare Auflösung ist dabei durch den Durchmesser des Laserspots beschränkt, der in
unserem Fall etwa 50 µm beträgt. Die Anzahl der inelastisch gestreuten Photonen
ist proportional zur Intensität der Spinwelle am Ort des Lasers.
Die zur Realisierung einer Zeitauflösung notwendigen Komponenten sind bereits in Abb. 3.6 angedeutet. Derselbe Pulsgenerator, der auch den Mikrowellenschalter (vgl. Kapitel 3.2.1) ansteuert, startet einen schnellen Zähler mit einer
Zeitbasis von 1,2 GHz. Dieser wird gestoppt, sobald ein inelastisch gestreutes
Photon registriert wird. Der aktuelle Zählerstand dient zur Adressierung einer
Speicherzelle eines Arrays, deren Inhalt um eins erhöht wird. Nach mehrmaliger
Wiederholung dieses Prozesses, gibt der Inhalt des Speicherarrays die zeitliche Intensitätsverteilung am Ort des Laserspots wieder [45,46]. Die zeitliche Auflösung
wird durch den Mehrfachdurchgang der Etalons bestimmt und beträgt hier etwa
2 ns. Abbildung 3.8 illustriert das beschriebene Verfahren.
Eine Kombination von orts- und zeitaufgelösten Messungen liefert eine dreidimensionale Matrix (zwei Ortskoordinaten, eine Zeitkoordinate). Diese Matrix
KAPITEL 3. EXPERIMENTELLE METHODEN
YIG
1. Triggersignal startet
Spinwelle und Zähler
Laser
2. Inelastisch gestreutes
Photon stopt Zähler
Start
Stop
Zähler
Intensität
Antenne
30
4. Speicherinhalt um
eins erhöhen
Zeitprofil der
Spinwelle
Speicherstellen (Zeit)
3. Zählerstand adressiert
Speicher
Abbildung 3.8: Schematische Darstellung der zeitaufgelösten BLS-Messung.
enthält die Anzahl der am jeweiligen Ort zur jeweiligen Zeit inelastisch gestreuten Photonen. Mit Hilfe eines Computerprogrammes3 können daraus die (zweidimensionalen) Intensitätsverteilungen der Spinwelle zu jedem Zeitpunkt bestimmt
und entweder als einzelne Bilder (wie zum Beispiel in Kapitel 4.2) oder als Filme
dargestellt werden.
3.5
Erweiterung zur phasenaufgelöste BrillouinLichtstreuspektroskopie
Der bisher vorgestellte BLS-Aufbau erlaubt nur die Bestimmung der Intensität
und nicht der Phase der Spinwelle, da beim Nachweis der inelastisch gestreuten
Photonen jegliche Phaseninformation verloren geht. Um trotzdem Informationen über die Phase des gestreuten Lichts und damit über die Phase der Spinwelle zu erhalten, wurde im Rahmen dieser Arbeit eine Erweiterung der Brillouin3 Entwickelt
versity of Kiev.
von Andrey Chumak und Oleksandr Dzyapko, National Taras Schevchenko Uni-
KAPITEL 3. EXPERIMENTELLE METHODEN
31
Lichtstreuspektroskopie aufgebaut, die phasenaufgelöste Messungen ermöglicht.
Dazu wird das inelastisch gestreute Licht mit einem kohärenten Referenzsignal gleicher Frequenz überlagert. Das daraus resultierende Interferenzbild enthält Informationen über Amplitude und Phase der betrachteten Spinwelle. Dieses
Prinzip wurde bereits bei Experimenten mit Mikrowellen eingesetzt und lieferte
dort gute Ergebnisse [4].
Der prinzipielle Aufbau der phasenaufgelösten Brillouin-Lichtstreuspektroskopie ist in Abb. 3.9 dargestellt. Zur Erzeugung des Referenzsignals wird ein Teil
des eingestrahlten Lichts frequenzverschoben. Dazu wird ein elektro-optischer
Modulator (vgl. Kapitel 3.6) verwendet, der mit derselben Mikrowellenquelle betrieben wird, die auch die Spinwellen erzeugt. Mit einem Abschwächer kann die
Intensität des Referenzsignals eingestellt werden. Ein Phasenschieber erlaubt die
Festlegung der Anfangsphase.
Abbildung 3.9: Aufbau der Phasenaufgelösten Brillouin-Lichtstreuspektroskopie.
Während bei Mikrowellenexperimenten das Referenzsignal und das Messsignal im Allgemeinen räumlich getrennt sind und erst nach dem Experiment
zusammengeführt werden, zeigt Abb. 3.9, dass bei dem hier verwendeten Aufbau der Strahlengang von Referenz- und Messsignal übereinander liegen. Dies ist
notwendig, da die Wellenlänge des verwendeten Lasers deutlich kürzer ist als die
Wellenlänge von Mikrowellen (532 nm gegenüber einigen Zentimetern). Daher
KAPITEL 3. EXPERIMENTELLE METHODEN
32
können bereits kleine Änderungen im Strahlengang, zum Beispiel durch thermische Ausdehnung oder Vibrationen beim Verschieben der Probe, das Interferenzbild stören.
Eine Kombination der Phasenauflösung mit der orts- und zeitaufgelösten
Brillouin-Lichtstreuspektroskopie (Kapitel 3.4) ist möglich und erlaubt die Darstellung der Phasenfronten einer propagierenden Spinwelle (vgl. Kapitel 4.3) oder
die Aufnahme von Phasenprofilen in einem festgelegten Punkt.
3.6
Elektro-optischer Modulator
Zur Erzeugung des frequenzverschobenen Referenzlichts wird der in Kapitel 2.7
beschriebene elektro-optische Effekt benutzt. Als Modulator wird ein LithiumNiobat-Kristall (LiNbO3 ) verwendet. Das Licht wird entlang der y-Achse eingestrahlt und ist entlang der z-Achse polarisiert. Das elektrische Wechselfeld liegt
in z-Richtung an (vgl. Abb. 3.10).
40 mm
LiNbO3
z
y
x
E = E0 sin (ωmt)
4 mm
4 mm
Abbildung 3.10: Aufbau des Elektro-optischen Modulators. Der LiNbO3-Kristall befindet
sich in einem Hohlraumresonator (hier aus Gründen der Übersichtlichkeit nicht dargestellt). Nach der Modulation hat das Licht zwei Seitenbänder mit ω ± ωm .
Aufgrund der notwendigen hohen Frequenz (einige GHz) der Modulation, ist
KAPITEL 3. EXPERIMENTELLE METHODEN
33
der Kristall in einen Hohlraumresonator [47] eingebaut. Dieser wird mit demselben Mikrowellensignal betrieben, das auch zur Anregung der Spinwellen verwendet wird (Referenzsignal in Abb. 3.3). So ist sichergestellt, dass das inelastisch
gestreute und das Referenzlicht kohärent sind.
Der Resonator wird auf die gewünschte Frequenz abgestimmt. Dabei ist zu
beachten, dass der Kristall eine hohe Dielektrizitätskonstante (ε ≈ 43 [28]) hat
und daher die Resonanzfrequenz beeinflusst. Die Abstimmung sollte deshalb für
den Resonator mit eingebauten Kristall erfolgen.
Im Rahmen dieser Arbeit wurden zwei Resonatoren aufgebaut, die auf verschiedene Frequenzen abgestimmt wurden. Abbildung 3.11 zeigt die gemessene Resonanz eines der verwendeten Resonatoren. Dazu wurde das vom Resonator reflektierte Signal gemessen. Die Resonanzfrequenz ist ν = 7,1275 GHz,
der Gütefaktor [47, 48] beträgt Q ≈ 440. Für den zweiten Resonator ergab sich
ν = 4,3536 GHz und Q ≈ 350. Da die Modulation sehr effektiv ist, ist es nicht unbedingt erforderlich, die exakte Resonanzfrequenz zu verwenden, gute Resultate
wurden im Experiment auch für Abweichungen von einigen 10 MHz erzielt.
5
0
Reflektiertes Signal [dB]
-5
-10
-15
-20
-25
-30
-35
-40
-45
-50
7,10
7,11
7,12
7,13
7,14
7,15
Frequenz [GHz]
Abbildung 3.11: Resonanz eines der verwendeten Resonatoren. Gemessen wurde
die vom Resonator reflektierte Mikrowellenleistung. Die Resonanzfrequenz beträgt
ν = 7,1275 GHz, für den Gütefaktor ergibt sich Q ≈ 440.
Wenn die Polarisation des einfallenden Lichts nicht exakt in die z-Richtung
KAPITEL 3. EXPERIMENTELLE METHODEN
34
des Kristalls zeigt (z.B. durch einen etwas verkippten Kristall), führt der elektrooptische Effekt des LiNbO3 zusätzlich zu einer geringen Polarisationsdrehung
[28]. Diese Drehung ist in diesem Fall allerdings hilfreich, da so sichergestellt ist,
dass das Referenzlicht eine Polarisationskomponente parallel zu der Polarisation
des inelastisch gestreuten Lichts hat und dadurch Interferenz möglich wird.
Die Interferenz findet dabei nur zwischen dem frequenzverschobenen und dem
inelastisch gestreuten Licht statt, da der elastisch gestreute Anteil durch das Interferometer ausgefiltert wird.
Eine alternative Möglichkeit den notwendigen Anteil an parallel polarisiertem
Licht zu erzeugen wird in Kapitel 4.3.3 vorgestellt.
Kapitel 4
Experimentelle Ergebnisse
4.1
Propagation von dipolaren Spinwellen durch ein
inhomogenes Feld
Die Propagation von Spinwellen in einem inhomogenen Feld wurde bereits in
den sechziger Jahren untersucht [1, 2, 49]. Neuere Untersuchungen zeigten, dass
das Oersted-Feld eines stromdurchflossenen Leiters bei geeigneter Polarität eine
Potentialbarriere erzeugt, die einen Teil der Spinwelle reflektiert [5, 50].
Alle bisherigen Untersuchungen beschränkten sich auf die Beobachtung der
Propagationseigenschaften der Welle, wie beispielsweise die Änderung der Gruppengeschwindigkeit, sowie Reflexion und Tunneleffekt. Im Rahmen dieser Arbeit
wird nun auch die Phasenänderung der Spinwelle bei Propagation durch ein lokal inhomogenes Feld behandelt. Die Inhomogenität wird durch einen Strompuls
erzeugt, der zu einem zusätzlichen Magnetfeld δH(z) führt, welches das Feld H0
lokal variiert. Als Leiter wird dabei ein Golddraht (Kapitel 4.1.3) oder ein Streifen
aus Kupfer verwendet (Kapitel 4.1.4 und Kapitel 4.1.5). Der Strom zur Erzeugung
des zusätzlichen Feldes und die Spinwelle werden gepulst (Wiederholfrequenz
1 kHz), um eine Erwärmung des YIG-Films zu vermeiden.
4.1.1 Ursache der Phasenverschiebung
Wie bereits in Kapitel 2.6.5 gezeigt wurde, verschiebt eine Änderung des magnetischen Feldes die Dispersionsrelation von dipolaren Spinwellen entlang der Frequenzachse (vgl. Abb. 2.5). Für eine feste Frequenz ω bedeutet das eine Veränderung des Wellenvektors k. Für BVMSW ist dieser Effekt in Abb. 4.1 dargestellt.
35
Frequenz [GHz]
KAPITEL 4. EXPERIMENTELLE ERGEBNISSE
36
H0
H1
H1 > H0
ω
Wellenvektor [cm−1 ]
k0 k1
Abbildung 4.1: Änderung des Wellenvektors einer BVMSW bei Änderung des Magnetfeldes.
Diese Änderung von k bewirkt eine Phasenverschiebung
l
∆ϕ =
∆k(z)dz,
(4.1)
0
wobei l die Länge der Inhomogenität und ∆k(z) = k(z) − k0 die lokale Änderung
des Wellenvektors durch die Inhomogenität ist1 .
Abbildung 4.2 veranschaulicht diesen Effekt. Dargestellt ist eine Spinwelle
(durchgezogene Linie) die durch ein Gebiet mit erhöhtem magnetischen Feld, das
zur Vereinfachung als stufenförmig angenommen wird, propagiert (grau hinterlegt). In diesem Gebiet wird der Betrag des Wellenvektors k vergrößert, das heißt
die Wellenlänge λ = 2π/k verkleinert. Nach Verlassen des Gebiets propagiert die
Welle mit ihrer ursprünglichen Wellenlänge weiter. Im Vergleich zu einer Welle, die nicht durch das erhöhte Feld beeinflusst wurde (gepunktete Linie), haben
sich die Positionen der Extrema verschoben. Diese räumliche Verschiebung ∆x
entspricht einer Phasenverschiebung ∆ϕ.
1 Die
Reflexion der Welle an den Grenzen der Inhomogenität wird hierbei nicht berücksichtigt.
KAPITEL 4. EXPERIMENTELLE ERGEBNISSE
37
∧
∆x = ∆ϕ
l
.
Amplitude [willkürliche Einheiten]
1
0.5
0
0.5
1
0
5
10
15
20
25
30
Abstand x [willkürliche Einheiten]
Abbildung 4.2: Verhalten einer BVMSW (durchgezogene Linie) bei Propagation durch
ein Gebiet mit erhöhtem Magnetfeld (grau hinterlegt). Die räumliche Verschiebung ∆x
der Extrema bezüglich der Welle ohne Beeinflussung durch das erhöhte Feld (gepunktete
Linie) entspricht einer Phasenverschiebung ∆ϕ. Die Reflexion der Welle an den Grenzen
der Inhomogenität ist aus Gründen der Übersichtlichkeit nicht dargestellt [27].
4.1.2 Versuchsaufbau
Zur Messung der Phasenverschiebung wurde der in Abb. 4.3 skizzierte Aufbau
verwendet.
Die erzeugten Mikrowellenpulse (vgl. Kapitel 3.2.1) werden mit Hilfe eines
Leistungsteilers in zwei gleiche Signale geteilt. Eines der Signale wird zur Eingangsantenne der Probe geleitet und dient zur Anregung der Spinwellen. Das
zweite Signal dient als Referenz und kann durch einen kalibrierten Phasenschieber beeinflusst werden. Ein zweiter Leistungsteiler dient als Mixer und führt das
Referenzsignal mit dem Signal der Ausgangsantenne zusammen, so dass beide
Signale interferieren. Das Interferenzbild wird, wie in Kapitel 3.2.2 beschrieben,
auf einem Oszilloskop dargestellt.
Zur Messung der Phasenverschiebung bei verschiedenen Stromstärken I wird
mit Hilfe des kalibrierten Phasenschiebers das Interferenzbild von I = 0 A wie-
KAPITEL 4. EXPERIMENTELLE ERGEBNISSE
38
YIG
GGG
Oszilloskop
ϕ
Leistungsteiler
Leistungsteiler
Abbildung 4.3: Aufbau zur Messung der Phasenverschiebung. Durch die Interferenz mit
einem Referenzsignal wird die Phasenänderung durch die Inhomogenität bestimmt.
derhergestellt. Die dazu benötigte Phasenverschiebung des Referenzsignals entspricht der Phasenverschiebung der Spinwelle, die durch die Feldinhomogenität
erzeugt wird.
Wird das Referenzsignal abgeschaltet (d.h. die Leistungsteiler entfernt) erlaubt
der beschriebene Aufbau auch eine direkte Messung der Amplitude der transmittieren Spinwelle, und durch den Vergleich mit der Amplitude bei I = 0 A die Bestimmung der relativen Transmission durch die Inhomogenität.
4.1.3 Propagation von
Backward“-Volumenmoden durch
”
eine starke Inhomogenität
Zur Erzeugung des zusätzlichen Magnetfeldes δH dient ein vom Strom I durchflossener Draht (Gold, Radius r = 12,5 µm, Strompulse der Länge 100 ns), der
direkt auf dem YIG-Film aufliegt (vgl. Abb. 4.4). Für das in der Filmebene erzeugte Feld gilt nach dem Ampèreschen Gesetz [9]
δH(z) =
2Ir
c(z2 + r2 )
.
(4.2)
Der Koordinatenursprung ist in der Mitte des Drahtes gewählt, z beschreibt die
Position in Propagationsrichtung, c ist die Vakuumlichtgeschwindigkeit. Die daraus resultierende Inhomogenität ist für einen Strom von I = ±0,6 A in Abb. 4.5
dargestellt.
Da der Draht direkt auf der Filmoberfläche aufliegt, wirkt er auch als Antenne. Ein Teil der Spinwelle wird daher bei der Propagation in Mikrowellen
umgewandelt und anschließend in die Umgebung abgestrahlt. Dies führt zu einer
zusätzlichen Dämpfung.
KAPITEL 4. EXPERIMENTELLE ERGEBNISSE
H0
39
I
δH
Abbildung 4.4: Aufbau der Probe zur Erzeugung einer starken Inhomogenität durch einen
stromdurchflossenen Draht. Der Draht erzeugt ein lokales Feld δH(z), das das Feld H0
absenkt oder erhöht.
0
δH[Oe]
-20
(a) I = −0,6 A
-40
-60
-80
-100
-0,20
-0,15
-0,10
-0,05
0,00
0,05
0,10
0,15
0,20
-0,05
0,00
0,05
0,10
0,15
0,20
δH[Oe]
100
80
(b) I = +0,6 A
60
40
20
0
-0,20
-0,15
-0,10
Position z [mm]
Abbildung 4.5: Zusätzliches magnetisches Feld δH(z) durch einen stromdurchflossenen
Draht. (a) I = −0,6 A, (b) I = +0,6 A.
KAPITEL 4. EXPERIMENTELLE ERGEBNISSE
40
Messung der Transmission
Für beide Polaritäten des Stroms (d.h. für Erhöhung und Absenkung des magnetischen Feldes) wurde die relative Transmission und die Phasenverschiebung durch
die Inhomogenität bei einer Spinwellenfrequenz von ω = 2π · 7,125 GHz für verschiedene Feldstärken H0 (und damit verschiedene Wellenvektoren k0 ) gemessen.
Die Länge der Spinwellenpulse beträgt 310 ns.
Die gemessene relative Transmission bei lokaler Absenkung des Feldes (vgl.
Abb. 4.6) zeigt das bereits aus [5, 50] bekannte Verhalten: der Abfall der Transmission ist im wesentlichen exponentiell, nur bei geringen Strömen und großen
Feldern (d.h. großen Wellenvektoren) tritt keine Änderung oder sogar eine Vergrößerung der Transmission auf.
1,1
1,0
1813 Oe
1818 Oe
1823 Oe
1833 Oe
1843 Oe
0,9
0,8
Transmission
0,7
0,6
0,5
0,4
0,3
0,2
0,1
0,0
0,0
0,5
1,0
1,5
2,0
Strom [A]
Abbildung 4.6: Relative Transmission bei lokaler Absenkung des magnetischen Feldes durch einen stromdurchflossenen Draht. Die Frequenz der Spinwellen beträgt
ω = 2π · 7,125 GHz.
Ursache für den exponentiellen Abfall ist das Ausbilden einer Tunnelbarriere,
da die Dispersionsrelation durch das zusätzliche Feld δH(z) so stark verschoben
wird, dass die Frequenz der propagierende Spinwelle außerhalb des für BVMSW
erlaubten Bereiches liegt (vgl. Gl. (2.48)). Je größer δH(z) wird, desto breiter
wird die Tunnelbarriere. Bei großen Wellenvektoren muss die Dispersionsrelation
KAPITEL 4. EXPERIMENTELLE ERGEBNISSE
41
stärker verschoben werden, um diesen verbotenen Bereich zu erreichen. Daher erfolgt in diesem Fall bei kleinen Strömen keine Absenkung der Transmission. Die
beobachtete Erhöhung tritt auf, da ein kleiner Strom den negativen Effekt, den der
Draht auch ohne Strom auf die Ausbreitung der Spinwelle hat, ausgleichen kann.
Außerdem führt eine Absenkung des Feldes zu einer Erhöhung der Gruppengeschwindigkeit und damit zu einer Abnahme der räumliche Dämpfung. Für eine
genauere Betrachtung dieses Effekts sei auf die oben zitierte Literatur verwiesen.
Die relative Transmission bei lokaler Erhöhung des Feldes (vgl. Abb. 4.7) zeigt
ein unerwartetes Verhalten. Obwohl bei einer Verschiebung der Dispersionsrelation nach oben für δH(z) H0 kein verbotener Bereich auftritt, und man daher
nur eine sehr geringe Reflexion (d.h. relative Transmission nahe eins) erwarten
würde, zeigt sich insbesondere für kleine Wellenvektoren eine deutliche Verringerung der Transmission im Bereich von 0,6 A. Für größere Ströme steigt die
Transmission wieder an. Eine Erklärung dieses Verhaltens wird im übernächsten
Abschnitt gegeben.
1,1
1,0
0,9
0,8
Transmission
0,7
0,6
0,5
1813 Oe
1818 Oe
1823 Oe
1829 Oe
0,4
0,3
0,2
0,1
0,0
0,0
0,5
1,0
1,5
2,0
Strom [A]
Abbildung 4.7: Relative Transmission bei lokaler Erhöhung des magnetischen Feldes
durch einen stromdurchflossenen Draht. Die Frequenz der betrachteten Spinwellen beträgt ω = 2π · 7,125 GHz.
KAPITEL 4. EXPERIMENTELLE ERGEBNISSE
42
Messung der Phasenverschiebung
Die gemessenen Phasenverschiebungen für verschiedene Felder und Ströme sind
in Abb. 4.8 dargestellt. Die Frequenz der betrachteten Spinwellenpulse beträgt
weiterhin ω = 2π · 7,125 GHz, die Pulslänge liegt zwischen 310 ns und 1,36 µs.
2,5
2,0
Phasenverschiebung [π]
1,5
δH < 0
1,0
0,5
1813 Oe
1818 Oe
1823 Oe
1829 Oe
1833 Oe
1843 Oe
0,0
δH > 0
-0,5
-1,0
-1,5
-2,0
-2,5
0,0
0,5
1,0
1,5
2,0
Strom [A]
Abbildung 4.8: Phasenverschiebung einer BVMSW durch das Feld eines stromdurchflossenen Drahtes. Abhängig vom Vorzeichen des Stroms wird die Dispersion nach oben oder
unten verschoben und damit eine positive oder negative Phasenverschiebung erzeugt. Die
Frequenz der betrachteten Spinwellen beträgt ω = 2π · 7,125 GHz.
Wie zu erwarten war, ist das Vorzeichen der Phasenverschiebung vom Vorzeichen des Stroms abhängig. Wird die Dispersionsrelation nach oben verschoben,
das heißt ist δH(z) > 0, wird der Betrag des Wellenvektors k(z) vergrößert. Da
hier BVMSW betrachtet werden sind die Wellenvektoren k0 (Wellenvektor außerhalb der Inhomogenität) und k(z) allerdings negativ, das heißt ∆k = k(z) − k0 ist
ebenfalls negativ. Nach Gl. (4.1) ergibt sich eine negativen Phasenverschiebung.
Analog erhält man bei nach unten verschobener Dispersion eine positive Phasenverschiebung. Außerdem ist zu erwähnen, dass der Betrag der Phasenverschiebung mit der Stromstärke streng monoton steigt. Auch dieses Verhalten entspricht
den Erwartungen, da ein höherer Strom zu einer Erhöhung von δH(z) und damit
zu einer stärkeren Änderung von k führt. Außerdem wird die Ausdehnung der
KAPITEL 4. EXPERIMENTELLE ERGEBNISSE
43
Inhomogenität l vergrößert. Beides führt nach Gl. (4.1) zu einer Erhöhung der
Phasenverschiebung.
Theoretisches Modell zur Beschreibung der Propagation durch eine starke
Inhomogenität
M.P. Kostylev2 entwickelte ein Modell, dass die beobachteten Effekte bei der Propagation einer Spinwelle durch eine starke Inhomogenität beschreibt.
Die Transmission wird darin durch die Interferenz mehrfachreflektierter Wellen beschrieben. Da hier allerdings keine stufenförmige Inhomogenität vorliegt,
sind Propagation und Reflexion der Spinwelle nicht voneinander getrennt. Daher
kann keine einfache physikalische Erklärung, wie zum Beispiel beim Kastenpotential in der Quantenmechanik gegeben werden.
Die wesentlichen Schritte der Berechnungen von Kostylev seien hier kurz wiedergegeben. Ausgangspunkt ist die Beschreibung der Propagation mittels eines
Green-Funktionsansatz wie in [5] durch
+∞
χ(z, ω)−1 mx (z) − Gxx (z, z )mx (z )dz = Aδ(z − z0 ).
(4.3)
−∞
χ ist das Diagonalelement des Polder-Suszeptibilitäts-Tensors (2.3), die z-Abhängigkeit ergibt sich da das Feld H von z abhängt.
Um diesen Ansatz zu erhalten, betrachtete Kostylev das dipolare Streufeld hS ,
das von m erzeugt wird. Wie in Kapitel 2.6.4 beschrieben, bildet nur die mx -Komponente eine Feld aus. Verwendet man wie in der Elektrostatik eine Greensche
Funktion [51] zur Berechnung von hS erhält man
+∞
hSx = Gxx (z, z )mx (z )dz .
(4.4)
−∞
Weiter gilt
↔
↔
m = χheff = χ(hS + hQ ),
(4.5)
mit dem Polder-Suszeptibilitäts-Tensors (2.3). Das effektive Feld heff setzt sich
aus dem Streufeld hS und dem Feld der anregenden Quelle (z.B. der Antenne) hQ
zusammen. Beide haben nur eine x-Komponente, daher vereinfacht sich Gl. (4.5)
zu
(4.6)
mx = χ(z, ω)(hSx + hQx ).
2 Elektrotechnische
lautern
Universität St. Petersburg, Russland und Technische Universität Kaisers-
KAPITEL 4. EXPERIMENTELLE ERGEBNISSE
44
Mit Gl. (4.4) ergibt sich
+∞
χ(z, ω)−1 mx (z) − Gxx (z, z )mx (z )dz = hQx .
(4.7)
−∞
Nimmt man eine am Ort z0 lokalisierte Quelle der Amplitude A an, ergibt sich
Gl. (4.3).
Kostylev gelang eine analytische Lösung von Gl. (4.3). Diese stimmt gut mit
der gemessenen Transmission und Phasenverschiebung überein (vgl. Abb. 4.9).
4.1.4 Propagation einer
Backward“-Volumenmode durch
”
eine schwache Inhomogenität
Für die technische Anwendung als stromgesteuerter Phasenschieber eignet sich
die in Kapitel 4.1.3 beschriebene Anordnung aufgrund der starken Änderung der
relativen Transmission nur sehr eingeschränkt. Folgende Überlegung zeigt, wie
eine Verbesserung der Transmission erreicht werden kann.
Wie durch Gl. (4.1) beschrieben, wird die Größe der Phasenverschiebung sowohl durch die Änderung des Wellenvektors ∆k und damit der Stärke des zusätzlichen Feldes δH(z) als auch durch die Länge der Inhomogenität l bestimmt. Die
schwache Transmission wird hauptsächlich durch die Reflexion der Welle an den
Grenzen der Inhomogenität und den daraus resultierenden Interferenzeffekten verursacht. Wenn daher diese Reflexion minimiert wird, sollte die Transmission in
der Nähe von eins liegen. Dies kann erreicht werden, indem der Draht durch einen
breiten Streifen ersetzt wird, da dann die Stromdichte und damit δH(z) abnimmt.
Gleichzeitig erhöht sich l, so dass trotzdem eine starke Phasenverschiebung erreicht werden kann.
Zur Erzeugung von δH(z) wird daher im Folgenden ein Streifen (Kupfer, Breite w = 1 mm, Strompulse der Länge 100 ns) als Leiter verwendet (vgl. Abb. 4.10).
Zu beachten ist, dass der Leiter jetzt auf der Unterseite des Substrates fixiert ist
und daher einen Abstand von d = 0,5 mm zum YIG-Film hat. Um die Ergebnisse direkt vergleichen zu können, werden weiterhin Spinwellenpulse der Frequenz
ω = 2π · 7,125 GHz verwendet. Die Pulslänge beträgt 310 ns.
Zur Berechnung des zusätzlichen Feldes in der Filmebene verwendet man das
Biot-Savart-Gesetz [9]
(r − r ) 3
1
j(r )
d r.
(4.8)
H(r) =
c
|r − r |
Dabei ist c die Vakuumlichtgeschwindigkeit und j die Stromdichte. Für das Feld
eines unendlich langen und dünnen Streifens in der Ebene des YIG-Films erhält
KAPITEL 4. EXPERIMENTELLE ERGEBNISSE
45
1,1
1,0
Experiment
Theorie
0,9
0,8
Transmission
0,7
0,6
0,5
0,4
0,3
0,2
0,1
0,0
-2,0
-1,5
-1,0
-0,5
0,0
0,5
1,0
1,5
2,0
Strom [A]
(a) Amplitude
1,0
Experiment
Theorie
0,5
Phasenverschiebung [π]
0,0
-0,5
-1,0
-1,5
-2,0
-2,5
-3,0
-2,0
-1,5
-1,0
-0,5
0,0
0,5
1,0
1,5
2,0
Strom [A]
(b) Phase
Abbildung 4.9: Berechnete und gemessene Transmission und Phasenverschiebung von
BVMSW bei Propagation durch eine starke Inhomogenität für H = 1813 Oe. Die berechneten Werte stimmen gut mit den gemessenen überein [52]. (a) Amplitude, (b) Phase.
KAPITEL 4. EXPERIMENTELLE ERGEBNISSE
H0
46
I
w = 1 mm
δH
Abbildung 4.10: Aufbau der Probe zur Erzeugung einer schwachen Inhomogenität durch
einen stromdurchflossenen Streifen. Der Streifen erzeugt ein lokales Feld δH(z), das das
Feld H0 absenkt oder erhöht.
man daraus
z − w2
z + w2
2I
− arctan
+ arctan
.
δH(z) =
cw
d
d
(4.9)
Der Koordinatenursprung ist in der Mitte des Streifens definiert, z beschreibt die
Position in Propagationsrichtung. Abb. 4.11 zeigt die resultierende Inhomogenität
für einen Strom von ±0,6 A. Im Vergleich zu Abb. 4.5 erkennt man die geringere
Stärke und die größere Ausdehnung der Inhomogenität.
Messung der Transmission
Abb. 4.12 zeigt die gemessene Transmission für beide Polaritäten. Im Vergleich
zur Propagation durch eine starke Inhomogenität (Abb. 4.6 und 4.7) erkennt man
eine deutliche Erhöhung der relativen Transmission von unter 20 % auf über 85 %
für alle betrachteten Ströme (I = 0 . . . 2 A). Dies entspricht zusätzlichen Verlusten
von unter 1 dB.
Messung der Phasenverschiebung
Die gemessenen Phasenverschiebungen sind in Abb. 4.13 dargestellt. Es fällt auf,
dass für alle betrachteten Felder, d.h. Wellenvektoren k0 , ∆ϕ(I) linear ist. Außerdem ist die Steigung ∆ϕ/I nahezu unabhängig vom Feld.
Eine Phasenverschiebung von π, wie sie zum Aufbau von Spinwellen-LogikGattern notwendig ist (vgl. Kapitel 4.1.6), wird in dieser Konstruktion im Bereich
von Iπ ≈ 0,9 A erreicht. Dieser Strom ist relativ hoch und kann, wie folgende
Überlegung zeigt, nicht wesentlich verringert werden:
KAPITEL 4. EXPERIMENTELLE ERGEBNISSE
47
0,0
(a) I = −0,6 A
δH[Oe]
-0,5
-1,0
-1,5
-2,0
-20
-15
-10
-5
0
5
10
15
20
-5
0
5
10
15
20
δH[Oe]
2,0
(b) I = +0,6 A
1,5
1,0
0,5
0,0
-20
-15
-10
Position z [mm]
Abbildung 4.11: Zusätzliches magnetisches Feld δH(z) durch einen stromdurchflossenen
Streifen (Breite w = 1 mm). Im Vergleich mit Abb. 4.5 fällt auf, dass das Feld des Streifens
schwächer als das des Drahtes, dafür aber stärker ausgedehnt ist (Die z-Achse ist hier
um einen Faktor 100 größer.) (a) I = −0,6 A, (b) I = +0,6 A.
1,0
0,9
0,9
Transmission
1,1
1,0
Transmission
1,1
0,8
0,8
0,7
0,7
0,6
0,6
0,5
0,5
1813 Oe
1818 Oe
1823 Oe
1833 Oe
1843 Oe
0,4
0,3
0,2
1813 Oe
1818 Oe
1823 Oe
1833 Oe
1843 Oe
0,4
0,3
0,2
0,1
0,1
0,0
0,0
0,0
0,5
1,0
1,5
Strom [A]
(a) Absenkung des Feldes
2,0
0,0
0,5
1,0
1,5
2,0
Strom [A]
(b) Erhöhung des Feldes
Abbildung 4.12: Relative Transmission bei (a) Absenkung, (b) Erhöhung des magnetischen Feldes durch einen stromdurchflossenen Streifen (ω = 2π · 7,125 GHz).
KAPITEL 4. EXPERIMENTELLE ERGEBNISSE
48
2,0
Phasenverschiebung [π]
1,5
1,0
1813 Oe
1818 Oe
1823 Oe
1833 Oe
1843 Oe
0,5
0,0
-0,5
-1,0
-1,5
Iπ
-2,0
0,0
0,5
1,0
1,5
2,0
Strom [A]
Abbildung 4.13: Phasenverschiebung einer BVMSW durch das Feld eines stromdurchflossenen Streifens (ω = 2π · 7,125 GHz).
Für die Änderung des Wellenvektors durch das zusätzliche Feld gilt [53]
∆k(z) ∼ δH(z).
(4.10)
Mit Gl. (4.1) erhält man daraus
l
∆k(z)dz ≈ l∆k ∼ lδH.
∆ϕ =
(4.11)
0
Verwendet man Gl. (4.9), so ergibt sich
∆ϕ ∼
I
l.
w
(4.12)
Da die Länge der Inhomogenität l proportional zur Breite des Streifens w ist,
erkennt man, dass die Phasenverschiebung nicht von der Breite des Streifens
abhängig ist. Eine Erhöhung der Stromdichte I/w wird durch eine Verringerung
der Ausdehnung des zusätzlichen Feldes kompensiert. Daher ist in der BVMSWGeometrie eine Verringerung von Iπ nicht möglich.
KAPITEL 4. EXPERIMENTELLE ERGEBNISSE
49
4.1.5 Strom-induzierte Phasenverschiebung einer DamonEshbach-Mode
Geht man zur MSSW Geometrie über, so ist die Ausdehnung l von δH(z) nicht
mehr von der Streifenbreite w abhängig (vgl. Abb. 4.14). Daher kann das
Magnetfeld über die gesamte Propagationslänge der Spinwelle erhöht oder abgesenkt werden, ohne die Stromdichte und damit δH zu vermindern.
Zur Erzeugung von δH wird ein Kupferstreifen der Breite w = 2 mm parallel
zum YIG-Film auf der Unterseite des Substrats angebracht. Das zusätzliche Feld
ist dann von z unabhängig. Um diese Messung mit den vorherigen vergleichbar
zu machen, werden Spinwellenpulse derselben Frequenz (ω = 2π · 7,125 GHz)
verwendet. Die Pulslänge beträgt 400-700 ns.
H0
δH
l
I
w = 2 mm
Abbildung 4.14: Aufbau der Probe zur Erzeugung einer Phasenverschiebung in MSSW
Geometrie.
Abbildung 4.15 zeigt die gemessene Phasenverschiebung für I = 0,32 A und
H0 = 1810 Oe in Abhängigkeit von der Strompulslänge und damit der Zeitdauer
des zusätzlichen Feldes δH. Es fällt auf, dass die Phasenverschiebung für Strompulslängen ab etwa 300 ns gesättigt ist. Diese Zeit entspricht der Propagationsdauer des Spinwellenpulses zwischen den beiden Antennen. Eine weitere Verlängerung hat daher keinen Einfluss mehr, da die zu beeinflussende Spinwelle bereits
die Ausgangsantenne erreicht hat.
Für die Messung der Phasenverschiebung in Abhängigkeit von der Stromstärke
I und dem magnetischen Feld H0 wurde daher eine Strompulslänge von 310 ns
gewählt.
Wie zu erwarten war, ist die Phasenänderung (vgl. Abb. 4.16) deutlich größer
als in Kapitel 4.1.4 . Iπ beträgt hier etwa 0,32 A und damit nur etwa ein Drittel des
für die BVMSW-Geometrie nötigen Stroms. Dieser Strom kann weiter reduziert
werden, indem man die Breite des Kupferstreifens bis auf die Breite des YIGFilms reduziert und damit die Stromdichte erhöht.
KAPITEL 4. EXPERIMENTELLE ERGEBNISSE
50
0,1
0,0
-0,1
Phasenverschiebung [π]
-0,2
-0,3
-0,4
-0,5
-0,6
-0,7
-0,8
-0,9
-1,0
-1,1
0
50
100
150
200
250
300
350
Strompulslänge [ns]
Abbildung 4.15: Phasenverschiebung einer MSSW bei Veränderung der Zeitdauer innerhalb der das zusätzliche Feld δH anliegt (ω = 2π · 7,125 GHz, I = 0,32 A, H0 = 1810 Oe).
Neben dem deutlich reduzierten Strom Iπ ist ein weiterer Vorteil dieses Aufbaus, dass es keine Inhomogenität mehr gibt, da das Feld über die gesamte Propagationslänge geändert wird, so dass auch keine Stufen im Feld existieren, an
denen die Spinwelle reflektiert werden könnte. Eine geringe Änderung der Transmission ergibt sich trotzdem, da die Anregung durch Mikrowellen für kleinere
Wellenlängen weniger effektiv ist. Außerdem ändert sich die Gruppengeschwindigkeit der Spinwelle und damit auch die Aufenthaltsdauer im Medium. Daher
ändert sich auch die räumliche Dämpfung. Beide Effekte können zu zusätzlichen
Verlusten führen, die allerdings, wie schon im Fall von BVMSW, unter 1 dB liegen.
KAPITEL 4. EXPERIMENTELLE ERGEBNISSE
51
2,5
2,0
Phasenverschiebung [π]
1,5
1,0
1790 Oe
1800 Oe
1805 Oe
1810 Oe
1815 Oe
1820 Oe
0,5
0,0
-0,5
-1,0
-1,5
-2,0
Iπ
0,0
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
Strom [A]
Abbildung 4.16: Phasenverschiebung einer MSSW bei Veränderung des zusätzlichen Feldes δH(z) (ω = 2π · 7,125 GHz).
4.1.6 Spinwellen-Logik-Gatter
Schon in früheren Veröffentlichungen [54,55] wurden Konzepte zum Aufbau magnetischer Logik entwickelt. Hier soll nun gezeigt werden, wie ein Logik-Gatter
auf der Basis von Spinwellen aufgebaut werden kann [53].
XNOR-Gatter
Der prinzipielle Aufbau eines XNOR-Gatters (Exclusive Not OR auch Äquivalenz
genannt) ist in Abb. 4.17 dargestellt. Die Ströme I1 und I2 entsprechen dabei den
∧
∧
binären Eingängen (0 A = 0, Iπ = 1). Als Ausgang dient das Signal hinter dem
Mixer. Dabei wird destruktive Interferenz als 0, konstruktive Interferenz als 1 interpretiert. Ohne Strom sollen beide Teilsignale am Mixer mit gleicher Amplitude
und Phase eintreffen, das heißt beide Arme werden als identisch angenommen.
Unter diesen Bedingungen erhält man bei gleichen Eingangsströmen I1 = I2
konstruktive Interferenz am Mixer und somit eine logische 1 am Ausgang. Ist
I1 = 0 A und I2 = Iπ oder umgekehrt, beträgt die Phasendifferenz am Mixer π,
daher kommt es zu destruktiver Interferenz und einer logischen 0 am Ausgang.
KAPITEL 4. EXPERIMENTELLE ERGEBNISSE
52
I2
I1
Abbildung 4.17: Aufbau eines Spinwellen XNOR-Gatters. I1 und I2 entsprechen den logi∧
∧
schen Eingängen (0 A = 0, Iπ = 1). Als Ausgang dient das Signal hinter dem Mixer.
Eingänge
I1
Ausgang
I2
0
(0)
0
(0)
1
0
(0)
Iπ
(1)
0
Iπ
(1)
0
(0)
0
Iπ
(1)
Iπ
(1)
1
Tabelle 4.1: Wahrheitstabelle des XNOR-Gatters.
Dieses Verhalten (vgl. Tab. 4.1) entspricht einem XNOR-Gatter. Wird nur einer
der beiden Eingänge verwendet, kann das Gatter auch als NOT-Gatter verwendet
werden.
Abbildung 4.18 zeigt die ersten Messungen an einem XNOR-Gatter. Die Abbildung zeigt die Mikrowellenpulse am Ausgang des Mixers, die Belegung der
Eingänge ist in den Bildern angegeben.
Die Ausgangssignale können deutlich als logische 0 und 1 identifiziert werden.
Die starken Störungen am Ende der Pulse (in der Abbildung grau hinterlegt) wurden durch den verwendeten Schalter verursacht, da dieser einen leicht abfallenden
Strompuls liefert. Die Störung werden daher nur bei den Messungen beobachtet,
bei denen mindestens eine logische 1 am Eingang anliegt.
NAND-Gatter
Erweitert man das XNOR-Gatter um jeweils einen schmalen Leiter in beiden Armen, erhält man ein NAND-Gatter (Not AND, vgl. Abb. 4.19). Es wird weiterhin
60
55
50
45
40
35
30
25
20
15
10
5
0
750
0
1
=
800
1
1
850
=
800
850
950 1000 1050 1100 1150 1200
60
55
50
45
40
35
30
25
20
15
10
5
0
750
950 1000 1050 1100 1150 1200
60
55
50
45
40
35
30
25
20
15
10
5
0
750
0
900
Intensität [mV]
60
55
50
45
40
35
30
25
20
15
10
5
0
750
1
900
Intensität [mV]
Intensität [mV]
Intensität [mV]
KAPITEL 4. EXPERIMENTELLE ERGEBNISSE
Zeit [ns]
1
0
53
=
800
0
0
850
=
800
850
0
900
950 1000 1050 1100 1150 1200
1
900
950 1000 1050 1100 1150 1200
Zeit [ns]
Abbildung 4.18: Erste Messungen an einem XNOR-Gatters. Die starken Änderungen
des Ausgangssignals in dem grau hinterlegten Bereich wurden durch den verwendeten
Schalter verursacht. Dieser liefert einen leicht abfallenden Strompuls.
angenommen, dass beide Arme absolut identisch sind. Das heißt beide Signale
haben am Mixer gleiche Amplitude und Phase, wenn keine Ströme fließen. Als
Eingänge dienen jetzt die Ströme an den schmalen Leitern. Wie Abb. 4.7 zeigt,
existiert für ein geeignetes Feld ein Strom I1 , der dazu führt, dass die relative
Transmission bis fast auf Null zurückgeht. Dieser Effekt wird hier ausgenutzt. Es
∧
soll weiterhin 0 A = 0 gelten. Die logische 1 wird durch den Strom I1 repräsentiert.
Die beiden breiten Leiter werden mit einem konstanten Strom IS betrieben, der
eine Phasendifferenz von π/3 zwischen den beiden Signalen erzeugt. Dies führt
dazu, dass die Amplitude des Signals hinter dem Mixer gleich der Amplitude der
beiden Einzelsignale ist.
Liegt eine logische 1 an einem Eingang an, wird die Spinwelle in dem entsprechenden Arm fast vollständig abgeschwächt. Strom an einem der beiden Eingänge
ändert dabei aufgrund der eingestellten Phasendifferenz nichts an der Amplitude
des Ausgangssignals, während Strom an beiden Eingängen dieses stark reduziert.
Interpretiert man die starke Amplitude als logische 1 und die reduzierte Amplitude als logische 0, erhält man ein NAND-Gatter (vgl. Tab. 4.2). Für die Funktion
KAPITEL 4. EXPERIMENTELLE ERGEBNISSE
54
IS
I2
I1
IS
Abbildung 4.19: Aufbau eines Spinwellen NAND-Gatters. I1 und I2 entsprechen den logi∧
∧
schen Eingängen (0 A = 0, Iπ = 1). Als Ausgang dient das Signal hinter dem Mixer.
dieses Gatters ist es dabei unerheblich, wie die Phasendifferenz zwischen den beiden Armen erzeugt wird. Da sie nicht verändert werden muss, wäre also auch ein
konstruktionsbedingter Phasenunterschied (z.B. verschiedene Längen der beiden
Arme oder fest installierte mechanische Phasenschieber) möglich.
Ausgang
Eingänge
I1
I2
0
(0)
0
(0)
1
0
(0)
Iπ
(1)
1
Iπ
(1)
0
(0)
1
Iπ
(1)
Iπ
(1)
0
Tabelle 4.2: Wahrheitstabelle des NAND-Gatters.
Abbildung 4.20 zeigt Messungen, die an einem NAND-Prototype durchgeführt
wurden. Dargestellt ist der Mikrowellenpuls am Ausgang des Gatters. Die Belegung der logischen Eingänge ist in den Bildern angegeben.
Es ist gelungen, das Signal für eine logische 1 an beiden Eingängen vollständig
zu unterdrücken. In allen anderen Fällen kann ein Puls am Ausgang beobachtet
werden. Die Unterschiede in den Pulsformen werden durch die nicht absolut identischen Interferometerarme verursacht. Trotzdem können die Ausgangssignale
deutlich als logische 1 identifiziert werden.
KAPITEL 4. EXPERIMENTELLE ERGEBNISSE
0
1
Intensität [mV]
45
40
50
&
1
35
30
25
20
15
10
5
40
&
1
35
30
25
20
15
10
5
0
0
50
100 200 300 400 500 600 700 800 900 1000
1
1
45
40
0
50
&
0
35
30
25
20
15
10
5
100 200 300 400 500 600 700 800 900 1000
0
0
45
Intensität [mV]
0
Intensität [mV]
1
0
45
Intensität [mV]
50
55
40
&
1
35
30
25
20
15
10
5
0
0
0
100 200 300 400 500 600 700 800 900 1000
Zeit [ns]
0
100 200 300 400 500 600 700 800 900 1000
Zeit [ns]
Abbildung 4.20: Prototyp eines NAND-Gatters. Liegt eine logische 1 an beiden
Eingängen an, wird das Ausgangssignal vollständig unterdrückt. In allen anderen Fällen
kann ein deutlicher Puls am Ausgang beobachtet werden.
KAPITEL 4. EXPERIMENTELLE ERGEBNISSE
4.2
56
Tunneln von Spinwellen durch eine mechanische
Lücke
Nachdem bisher in der Literatur nur das Tunneln einer Spinwelle durch ein Gebiet
mit einem abgesenkten magnetischen Feld untersucht wurde (vgl. [5,50]), soll hier
nun das Tunneln durch eine mechanische Lücke im YIG-Film untersucht werden.
4.2.1 Tunneln durch eine Lücke
Zur Untersuchung dieses Effekts wurde eine Probe mit einer 20 µm breiten Lücke
im YIG-Film verwendet (vgl. Abb. 4.21). Wie in Kapitel 3.2.1 beschrieben werden Spinwellenpulse der Länge 200 ns in diesem Film angeregt. Abbildung 4.22
zeigt BLS-Messungen für zwei verschiedene Felder. Die Daten wurden auf den
Maximalwert zum jeweiligen Zeitpunkt normiert. Dargestellt sind lineare Falschfarbendarstellungen der Spinwellenintensität.
H0
20 µm
YIG
GGG
Abbildung 4.21: Probe zur Untersuchung des Tunnelns durch eine mechanische Lücke.
Wie deutlich zu erkennen ist, wird der größte Teil der Spinwelle an der Lücke
reflektiert, was zur Ausbildung einer stehenden Welle vor der Lücke führt. Ein
kleiner Teil tunnelt allerdings durch die Lücke und propagiert danach weiter. Dieser Anteil ist für die Spinwelle mit der kleineren Wellenlänge deutlich kleiner, da
diese Welle stärker von der Lücke beeinflusst wird.
4.2.2 Tunneln durch zwei Lücken
Im Folgenden wird ein YIG-Film mit zwei Lücken der Breite 20 µm im Abstand
von 1 mm untersucht. Es wurden Spinwellenpulse der Länge 250 µs bei einem
Feld von 1839 Oe angeregt. Die Frequenz betrug ν = 7,125 GHz. Abbildung 4.23
KAPITEL 4. EXPERIMENTELLE ERGEBNISSE
Lücke
57
Lücke
max
min
(a) H = 1835 Oe
(b) H = 1846 Oe
Abbildung 4.22: Propagation einer Spinwelle durch eine mechanische Lücke der Breite
20 µm. Die Bilder zeigen eine ortsaufgelöste Falschfarbendarstellung der Spinwellenintensität zu verschiedenen Zeiten. ν = 7,125 GHz, Pulslänge 200 ns, (a) H0 = 1835 Oe, (b)
H0 = 1846 Oe.
KAPITEL 4. EXPERIMENTELLE ERGEBNISSE
58
zeigt eine BLS-Messung an dieser Probe. Die dargestellten Daten wurden auf den
Maximalwert zum jeweiligen Zeitpunkt normiert.
Lücke
Lücke
Lücke
Lücke
max
min
Abbildung 4.23: Propagation einer Spinwelle durch zwei mechanische Lücken der Breite
20 µm. Es ist deutlich zu erkennen, dass die Welle für über 500 ns zwischen den beiden
Lücken eingeschlossen bleibt. H0 = 1839 Oe, ν = 7,125 GHz, Pulslänge 250 ns.
Es ist deutlich zu erkennen, dass eine Teil des Spinwellenpulses zwischen den
beiden Lücken eingeschlossen wird und über 500 ns erhalten bleibt. Dabei bildet sich zwischen den beiden Lücken ein Interferenzmuster aus, da die Länge des
Pulses größer ist als der Abstand zwischen den beiden Lücken. Das Verhalten in
diesem Bereich entspricht dem eines Resonators, der nicht mit der Resonanzfrequenz betrieben wird.
KAPITEL 4. EXPERIMENTELLE ERGEBNISSE
4.3
59
Erste Tests der phasenaufgelösten BrillouinLichtstreuspektroskopie
Im Folgenden sollen nun einige erste Messungen mit der in Kapitel 3.5 vorgestellten phasenaufgelösten Brillouin-Lichtstreuspektroskopie präsentiert werden.
Beobachtet wurden zunächst Spinwellen, die ohne äußere Beeinflussung (z.B. lokal geänderte Felder oder Lücken im Film) propagierten.
4.3.1 Phasenaufgelöste Brillouin-Lichtstreuspektroskopie an
cw-Spinwellen
Die ersten Messungen wurden mit kontinuierlichen Spinwellen durchgeführt. Die
erhaltenen Ergebnisse sind in Abb. 4.24 dargestellt.
max
min
(a) H0 = 907 Oe
(b) H0 = 930 Oe
Abbildung 4.24: Phasenaufgelöste Brillouin-Lichtstreuspektroskopie an cw-Spinwellen
der Frequenz ω = 2π · 4,3362 GHz. Obere Reihe: Ohne Referenzsignal. Untere Reihe:
Mit Referenzsignal (a) H0 = 907 Oe, (b) H0 = 930 Oe.
Die oberen Bilder zeigen die Intensität der Spinwelle in einer linearen Falschfarbendarstellung. Die Abnahme der Intensität kommt durch Dämpfung zustande. Die unteren Bilder zeigen Messungen mit zugeschaltetem Referenzsignal.
Die Phasenfronten der Welle sind deutlich zu erkennen. In Übereinstimmung mit
der Dispersionsrelation für BVMSW reduziert sich der Abstand zwischen den
Phasenfronten (d.h. die Wellenlänge λ) für das größere Feld. Der Effekt der
Dämpfung ist hier nicht so ausgeprägt, da für die Messung die Amplitude und
nicht die Intensität der Spinwelle maßgeblich ist.
Es fällt allerdings auf, dass die Interferenz direkt an der Eingangsantenne sehr
schwach ist. Kontrollmessungen haben gezeigt, dass bei der verwendeten Probe
KAPITEL 4. EXPERIMENTELLE ERGEBNISSE
60
das transmittierte Laserlicht in diesem Bereich deutlich abgeschwächt wird und
dadurch auch die Intensität des Referenzsignals und damit der Kontrast der Messung reduziert wird.
Weiterhin fällt auf, dass die gemessenen Intensität in keinem der Minima bis
auf null zurückgeht. Ursache hierfür ist, dass (wie in Kapitel 3.6 beschrieben)
nur ein geringer Teil des frequenzverschobenen Lichts dieselbe Polarisation wie
das inelastisch gestreute Licht hat3 . Um trotzdem eine deutliche Interferenz zu
erhalten, ist es daher erforderlich, für das Referenzsignal eine hohe Intensität zu
wählen, so dass ein Teil des senkrecht zum Polarisator polarisierten Lichts registriert wird und somit ein konstanter Signaluntergrund erzeugt. Eine Lösung dieses
Problems wird in Kapitel 4.3.3 vorgestellt.
4.3.2 Phasenaufgelöste Brillouin-Lichtstreuspektroskopie an
Spinwellen-Pulsen
In den meisten Spinwellen Experimenten werden gepulste Signale verwendet. Daher ist es wichtig zu zeigen, dass die phasenaufgelöste Brillouin-Lichtstreuspektroskopie auch unter diesen Bedingungen funktioniert.
max
min
(a) ohne Referenzsignal
(b) mit Referenzsignal
Abbildung 4.25: Phasenaufgelöste Brillouin-Lichtstreuspektroskopie an 30 ns Spinwellenpulsen der Frequenz ω = 2π · 4,3362 GHz. (H0 = 930 Oe) (a) ohne Referenzsignal,
(b) mit Referenzsignal.
3 Das
an den Spinwellen inelastisch gestreute Licht erfährt eine Polarisationsdrehung von π/2,
das im elektro-optischen Modulator frequenzverschobene Licht hingegen nicht.
KAPITEL 4. EXPERIMENTELLE ERGEBNISSE
61
Abbildung 4.25a zeigt den Puls ohne Referenzsignal. Die Messung wurde zu
jedem Zeitpunkt auf den jeweiligen Maximalwert normiert, daher ist die Dämpfung nicht erkennbar. Abbildung 4.25b zeigt die Messung mit Referenzsignal.
Der Kontrast ist geringer als in Abb. 4.24, da ein gepulstes Signal eine geringere
BLS-Zählrate erzeugt. Dies kann allerdings (falls gewünscht) durch eine längere
Messdauer ausgeglichen werden. Die Intensität in den Minima geht aus dem in
Kapitel 4.3.1 genannten Grund nicht bis auf null zurück.
Da das Referenzsignal kontinuierlich anliegt, erhält man bei der Messung
einen konstanten Signaluntergrund außerhalb des Pulses (vgl. Abb. 4.25).
4.3.3 Phasenaufgelöste Brillouin-Lichtstreuspektroskopie mit
verbessertem Kontrast
Zur Verbesserung des Kontrastes ist es nötig, den Anteil des senkrecht zum gestreuten Lichts polarisierten Referenzsignals zu reduzieren. Dazu wird vor dem
Mikrowellen-Resonator ein λ/4-Plättchen angebracht. Dieses erzeugt aus linear polarisiertem Licht zirkular oder elliptisch polarisiertes Licht [40], das heißt
Licht mit zwei orthogonalen Polarisationskomponenten. Diese werden gleich
stark durch den Resonator beeinflusst, so dass die notwendige Intensität des Referenzstrahls reduziert werden kann. Dadurch wird der Untergrund reduziert,
so dass die Signalintensität in den Minima bis auf nahezu null zurückgeht (vgl.
Abb. 4.26).
4.3.4 Phasenaufgelöste Brillouin-Lichtstreuspektroskopie an
der Probe mit mechanischer Lücke
Um die praktische Anwendung dieser neuen Technik zu zeigen, wurden phasenaufgelöste Messungen an der in Kapitel 4.2.1 verwendeten Probe mit mechanischer Lücke durchgeführt (vgl. Abb. 4.27). Die entsprechende BLS-Messung
ohne Referenzsignal wurde bereits in Abb. 4.22(b) dargestellt. Die Intensität des
Referenzsignals war an die Spinwellenintensität vor der Lücke angepasst.
Abbildung 4.27(a) und (b) unterscheiden sich nur durch die Normierung, die
zugrundeliegenden Daten sind identisch. Es fällt auf, dass trotz der geringen Spinwellenintensität hinter der Lücke, dort ein deutliches Interferenzmuster zu erkennen ist. Dies zeigt, dass es nicht unbedingt nötig ist, die Intensität des Referenzsignals an die Intensität der Spinwelle anzugleichen, um die Phasenfronten sichtbar
zu machen. Für quantitative Messungen kann das Resultat allerdings verbessert
werden, wenn diese Anpassung vorgenommen wird.
KAPITEL 4. EXPERIMENTELLE ERGEBNISSE
62
max
(a) H0 = 1838 Oe
min
(b) H0 = 1858 Oe
Abbildung 4.26: Phasenaufgelöste Brillouin-Lichtstreuspektroskopie an 200 µsSpinwellenpulsen der Frequenz ω = 2π · 7,125 GHz. Durch die Verwendung eines λ/4
Plättchen wird der Kontrast verbessert (d. h. die Intensität in den Minima verringert).
(a) H0 = 1838 Oe, (b) H0 = 1858 Oe.
max
min
(a) Normiert auf maximale Intensität
(b) Normiert auf Intensität hinter der
Lücke
Abbildung 4.27: Phasenaufgelöste Brillouin-Lichtstreuspektroskopie an der Probe mit
mechanischer Lücke. H0 = 1846 Oe, ω = 2π · 7,125 GHz. (a) Signal normiert auf die
maximale Intensität zum betrachteten Zeitpunkt. (b) Signal normiert auf Intensität hinter
der Lücke.
KAPITEL 4. EXPERIMENTELLE ERGEBNISSE
63
Vor der Lücke wird sowohl die einfallende als auch die reflektierte Spinwelle
beobachtet. Insbesondere im mittleren Bild (156,3 ns) wird diese Überlagerung
sehr deutlich, da die Phasenfronten der stehenden Welle zu erkennen sind.
Für die Spinwelle hinter der Lücke zeigt die Messung einen nicht konstanten Abstand zwischen den Phasenfronten. Ursache hierfür ist, dass die Spinwelle
durch das Tunneln sehr stark abgeschwächt wird und dadurch eine dem Rauschen
(z.B. thermische Spinwellen) vergleichbare Intensität hat. Dadurch wird das Interferenzbild ebenfalls durch das Rauschen beeinflusst und gibt daher nicht mehr
die genauen Phasenfronten des Signals wieder. Daher ist es nicht möglich, aus der
dargestellten Messung die Phasenverschiebung durch das Tunneln zu bestimmen.
Eine Erhöhung der Anfangsintensität ist hier nicht möglich, da dadurch vor der
Lücke nichtlineare Prozesse angeregt würden.
Bei größeren Spinwellenintensitäten tritt dieses Problem nicht auf, da die Amplitude des Rauschens in diesem Fall zu gering ist, um die Messung zu beeinflussen. Die phasenaufgelöste Brillouin-Lichtstreuspektroskopie liefert dann gute
Resultate, wie im letzten Kapitel gezeigt wurde.
Kapitel 5
Zusammenfassung und Ausblick
In dieser Arbeit wurde gezeigt, dass eine lokale Änderung des magnetischen Feldes durch einen stromdurchflossenen Leiter Phase und Amplitude der propagierenden Welle ändert. Ist die Änderung des Feldes hinreichend klein, wird die
Amplitude der Welle nur wenig geändert. Trotzdem wird (für eine ausgedehnte
Inhomogenität) die Phase deutlich beeinflusst. Phasenänderungen um π konnten
bei Backward“-Volumenmoden für Ströme im Bereich von 0,9 A und bei Ober”
flächenmoden im Bereich von 0,3 A erreicht werden.
Ist die Inhomogenität stark lokalisiert, treten hingegen deutliche Änderungen
der Amplitude auf. Das bereits aus [5,50] bekannte Tunneln von Spinwellen durch
ein lokal abgesenktes Feld konnte beobachtet werden.
Bei lokaler Erhöhung des Feldes wurde für kleine Wellenvektoren ein nicht
monotones Verhalten der relativen Transmission mit einem ausgeprägten Minimum beobachtet. M.P. Kostylev konnte zeigen, dass dieses Verhalten durch die
Interferenz zwischen mehrfachreflektierten Spinwellen verursacht wird. Theoretische Berechnungen zeigen eine gute Übereinstimmung mit den Messungen.
Basierend auf den aufgebauten stromgesteuerten Phasenschiebern konnte ein
neues Konzept zum Aufbau magnetischer Logik vorgestellt werden. Dieses basiert auf einem Spinwellen-Interferometer. Die logischen Eingangssignale beeinflussen die Phase oder die Amplitude von zwei Spinwellen, das Ausgangssignal
wird aus der Interferenz der beiden Wellen gewonnen. Es ist gelungen, einen auf
YIG basierenden Prototypen für ein XNOR- und ein NAND-Gatter aufzubauen
und zu testen.
Zur Weiterentwicklung dieses Konzepts ist der Aufbau von Interferometern
auf Permalloy Basis geplant. Da die Wellenlänge von Spinwellen in Permalloy
deutlich kürzer als in YIG ist (etwa 20 µm gegenüber etwa 300 µm), sollte dies zu
einer deutlichen Reduktion der notwendigen Größe führen.
64
KAPITEL 5. ZUSAMMENFASSUNG UND AUSBLICK
65
Mit Hilfe der orts- und zeitaufgelösten Brillouin-Lichtstreuspektroskopie wurde das Tunneln einer Spinwelle durch eine mechanische Lücke im YIG-Film untersucht. Dabei konnte beobachtet werden, dass ein geringer Teil der Spinwelle
die Lücke durchtunneln kann. Dieser Anteil steigt mit größer werdender Wellenlänge.
Wie schon bei der Untersuchung des Tunnelns durch eine lokale Inhomogenität [50], ist es gelungen, eine Spinwelle zwischen zwei mechanischen Lücken
einzuschließen. Die eingeschlossene Welle konnte noch nach einer halben Mikrosekunde nachgewiesen werden.
Werden die Tunnelbarrieren durch eine lokale Feldabsenkung erzeugt, sollte
die Konstruktion von dynamischen magnonischen Kristallen [56] möglich sein.
Diese sind das magnetische Analogon zu Photonischen Kristallen und sollte die
Ausbreitung von Spinwellen in einem weiten Bereich beeinflussen.
Zur Untersuchung der Phase von Spinwellen wurde eine Erweiterung der ortsund zeitaufgelösten Brillouin-Lichtstreuspektroskopie in Betrieb genommen. Diese erlaubt durch die Interferenz zwischen dem inelastisch gestreuten Licht und
einem Referenzsignal die Darstellung der Phasenfronten und -profile. Für lineare
Spinwellen ist es gelungen, die Phasenfronten abzubilden.
Weitere geplante Projekte mit der phasenaufgelösten Brillouin-Lichtstreuspektroskopie beinhalten die Untersuchung von nichtlinearen Spinwellen. Da die Aufnahme von Phasenprofilen in jedem beliebigen Punkt möglich ist, sollen insbesondere die Phaseneigenschaften von Solitonen (vgl. z.B. [57]) während der Entwicklung und Propagation beobachtet werden. Besonderes Interesse gilt dabei
den Moebius“-Solitonen [4, 58].
”
Literaturverzeichnis
[1] J. R. Eshbach, Spin-Wave Propagation and the Magnetoelastic Interaction
in Yttrium Iron Garnet, Physical Review Letters 8(9), 357 (1962).
[2] J. R. Eshbach, Spin-Wave Propagation and the Magnetoelastic Interaction
in Yttrium Iron Garnet, Journal of Applied Physics 34(4), 1298 (1963).
[3] M. A. Tsankov, M. Chen, C. E. Patton, Forward volume wave microwave envelope solitons in yttrium irin garnet films: Propagation, deca, and collision,
Journal of Applied Physics 76(7), 4274 (1994).
[4] S. O. Demokritov, A. A. Serga, V. E. Demidov, B. Hillebrands, M. P. Kostylev, B. A. Kalinikos, Experimental observation of symmetry-breaking nonlinear modes in an active ring, Nature 426, 159 (2003).
[5] S. O. Demokritov, A. A. Serga, A. André, V. E. Demidov, M. P. Kostylev, B. Hillebrands, A. N. Slavin, Tunnelling of Dipolar Spin Waves through
a Region of Inhomogeneous Magnetic Field, Physical Review Letters 93,
047201 (2004).
[6] A. S. Arrot, Magnetism in SI and Gaussian Units, in: J. A. C. Bland, B. Heinrich (Hg.) Ultrathin Magnetic Structures I, Springer-Verlag, Berlin, Heidelberg, New York (1994).
[7] A. G. Gurevich, G. A. Melkov, Magnetization Oscillations and Waves, CRC
Press, New York (1996).
[8] D. D. Stancil, Theory of Magnetostatic Waves, Springer-Verlag, New York,
Berlin, Heidelberg (1993).
[9] J. D. Jackson, Classical Electrodynamics, John Wiley & Sons, New York,
dritte Auflage (1998).
[10] W. Heisenberg, Zur Theorie des Ferromagnetismus, Zeitschrift für Physik
49, 619 (1928).
66
LITERATURVERZEICHNIS
67
[11] C. Cohen-Tannoudji, B. Diu, F. Laloë, Quantenmechanik, Band 2, Walter de
Gruyter, Berlin, New York, zweite Auflage (1999).
[12] S. Chikazumi, Physics of Ferromagnetism, Oxford University Press, New
York, zweite Auflage (1999).
[13] A. Aharoni, Introduction to the Theory of Ferromagnetism, Clarendon Press,
Oxford, zweite Auflage (2001).
[14] H. Haken, H. C. Wolf, Atom- und Quantenphysik, Springer-Verlag, Berlin,
Heidelberg, New York, 7. Auflage (2001).
[15] L. Landau, E. Lifshitz, On the theory of the dispersion of magnetic permeability in ferromagnetic bodies, Physikalische Zeitschrift der Sowjetunion 8,
153 (1935).
[16] T. L. Gilbert, A phenomenological theory of damping in ferromagnetic materials, IEEE Transactions on Magnetics 40(6), 3443 (2004).
[17] W. Nolting, Quantenmechanik - Methoden und Anwendungen, Band 5/2 von
Grundkurs Theoretische Physik, Springer-Verlag, Berlin, Heidelberg, New
York, fünfte Auflage (2004).
[18] B. Hillebrands, S. Blügel, Magnetismus, in: Festkörper, Band 6 von Bergmann, Schäfer: Lehrbuch der Experimentalphysik, de Gruyter, Berlin, zweite Auflage (2005).
[19] H. Ibach, H. Lüth, Festkörperphysik, Springer-Verlag, Berlin, Heidelberg,
New York, 6. Auflage (2002).
[20] R. W. Damon, J. R. Eshbach, Magnetostatic Modes of a Ferromagnetic Slab,
Journal of Applied Physics 31(5), 104S (1960).
[21] R. W. Damon, J. R. Eshbach, Magnetostatic Modes of a Ferromagnetic Slab,
Journal of Physics and Chemistry of Solids 19(3/4), 308 (1960).
[22] L. R. Walker, Magnetostatic Modes in Ferromagnetic Resonance, Physical
Review 105(2), 390 (1957).
[23] C. Kittel, Interpretation of anomalous larmor frequencies in ferromagnetic
resonance experiments, Physical Review 71(4), 270 (1947).
[24] C. Kittel, On the theory of ferromagnetic resonance absorption, Physical
Review 73(2), 155 (1948).
LITERATURVERZEICHNIS
68
[25] J. H. van Vleck, Concerning the theory of ferromagnetic ressonance absorption, Physical Review 78(3), 266 (1950).
[26] B. A. Kalinikos, A. N. Slavin, Theory of dipol-exchange spin wave spectrum
for ferromagnetic films with mixed exchange boundary conditions, Journal
of Physics C: Solid State Physics 19, 7013 (1986).
[27] C. Bayer, persönliche Mitteilung.
[28] A. Yariv, Optical Electronics in Modern Communications, Oxford University Press, New York, fünfte Auflage (1997).
[29] M. Abramowitz, I. A. Stegun (Hg.) Handbook of Mathematical Functions,
Dover Puplications, Inc., New York (1965).
[30] I. N. Sneddon, Special functions of mathematical physics and chemistry,
Longman, dritte Auflage (1980).
[31] M. Rohmer, Untersuchungen an mikrowellenangeregten Spinwellen, Diplomarbeit, Fachbereich Physik, Universität Kaiserslautern (1998).
[32] G. Nimtz, Mikrowellen - Einführung in Theorie und Anwendung, BI Wissenschaftsverlag, Manheim, Wien, Zürich, zweite Auflage (1990).
[33] D. V. Morgan, M. J. Howes (Hg.) Microwave solis state devices and applications, Peter Peregrinus Ltd., Stevenage, UK, New York (1980).
[34] S. O. Demokritov, B. Hillebrands, A. N. Slavin, Brillouin Light Scattering
Studies of Confined Spin Waves: Linear and Nonlinear Confinement, Physics
Reports 348(6) (2001).
[35] T. Wittkowski, Brillouin-Lichtstreuuntersuchungen an Bornitridschichten,
Dissertation, Fachbereich Physik, Universität Kaiserslautern (2002).
[36] B. Hillebrands, Brillouin light scattering from layered magnetic structures,
in: M. Cardona, G. Güntherodt (Hg.) Light scattering in solids VII. Crystal field and magnetic excitations, Band 75 von Topics in applied physics,
Springer-Verlag, Berlin, Heidelberg, New York (2000).
[37] P. A. Fleury, R. Loudon, Scattering of Light by One- and Two-Magnon Excitations, Physical Review 166(2), 514 (1968).
[38] J. R. Sandercock, Trends in Brillouin Scattering: Studies of Opaque Materials, Supported Films, and Central Modes, in: M. Cardona, G. Güntherodt
(Hg.) Light scattering in solids III. Recent Results, Band 51 von Topics in
applied physics, Springer-Verlag, Berlin, Heidelberg, New York (1982).
LITERATURVERZEICHNIS
69
[39] K. A. Jones, Optoelektronik, Wiley-VCH, Weinheim, New York, Basel,
Cambridge (1992).
[40] E. Hecht, Optik, Oldenbourg, München, Wien, vierte Auflage (2005).
[41] J. R. Sandercock, A high resolution, high contrast interferometer, and its application to Brillouin scattering from magnetic materials, in: M. Balkanski
(Hg.) Proceedings of the 3rd International Conference on Light Scattering
in Solids, Campinas, Brazil, 25-30 July 1975, S. 219, Flammarion Sciences,
Paris (1976).
[42] S. M. Lindsay, M. W. Anderson, J. R. Sandercock, Construction and alignment of a high performance multipass vernier tandem Fabry-Perot interferometer, Review of Scientific Instruments 52(10), 1478 (1981).
[43] R. Mock, B. Hillebrands, R. Sandercock, Construction and alignment of
a high performance multipass vernier tandem Fabry-Perot interferometer,
Journal of Physics E: Scientific Instruments 20, 656 (1987).
[44] B. Hillebrands, Progress in multipass tandem Fabry-Perot interferometry:
I. A fully automated, easy to use, self-aligning spectrometer with increased
stability and flexibility, Review of Scientific Instruments 70(3), 1589 (1998).
[45] O. Büttner, Zeit- und ortsaufgelöste Untersuchungen mikrowellenangergter Spinwellen in dünnen magnetischen Schichten, Dissertation, Fachbereich
Physik, Universität Kaiserslautern (1999).
[46] O. Büttner, M. Bauer, S. O. Demokritov, B. Hillebrands, Y. S. Kivshar,
V. Grimalski, Y. Rapport, A. N. Slavin, Linear and nonlinear diffraction
of dipolar spin waves in yttrium iron garnet films observed by space- and
time-resolved Brillouin light scattering, Physical Review B 61(17), 11576
(2000).
[47] D. Kajfez, P. Guillon (Hg.) Dielectric Resonators, Vector Fields, Oxford,
Mississippi (1990).
[48] R. S. Kwok, J.-F. Liang, Characterization of high-Q resonators for
miceowave-filter applications, IEEE Transactions on Microwave Theory and
Techniques 47(1), 111 (1999).
[49] R. W. Damon, H. van de Vaart, Propagation of Magnetostatic Spin Waves
at Microwave Frequencies. II. Rods, Journal of Applied Physics 37(6), 2445
(1966).
LITERATURVERZEICHNIS
70
[50] A. André, Nichtlineare Spinwellenpakete in Yttrium-Eisen-Granat-Filmen
mit kontrollierten Phaseneigenschaften, Diplomarbeit, Fachbereich Physik,
TU Kaiserslautern (2004).
[51] K. Y. Guslienko, S. O. Demokritov, B. Hillebrands, A. N. Slavin, Effective
dipolar boundary conditions for dynamic magnetization in thin magnetic
stripes, Physical Review B 66, 132402 (2002).
[52] M. P. Kostylev, persönliche Mitteilung.
[53] M. P. Kostylev, A. A. Serga, T. Schneider, B. Leven, B. Hillebrands, Spinwave logical gates, Applied Physics Letters 87, 153501 (2005).
[54] R. P. Cowburn, M. E. Welland, Room Temperature Magnetic Quantum Cellular Automata, Science 287, 1466 (2000).
[55] R. Richter, L. Bär, J. Wecker, G. Reiss, Nonvolatile field programmable spinlogic for reconfigurable computing, Applied Physics Letters 80(7), 1291
(2002).
[56] S. A. Nikitov, P. Tailhades, C. S. Tsai, Spin waves in periodic magnetic
structures - magnonic crystals, Journal of Magnetism and Magnetic Materials 236, 320 (2001).
[57] N. G. Kovshikov, B. A. Kalinikos, C. E. Patton, E. S. Wright, J. M. Nash,
Formation, propagation, reflection, and collision of microwave envelope solitons in yttrium iron garnet films, Physical Review B 54(21), 15210 (1996).
[58] A. A. Serga, M. P. Kostylev, B. A. Kalinikos, S. O. Demokritov, B. Hillebrands, H. Benner, Parametric Generation of Solitonlike Spin-Wave Pulses
in Ring Resonators Based on Ferromagnetic Films, JETP Letters 77(6), 300
(2003).
Danksagung
Am Ende sei all denen gedankt, die durch ihre Mitarbeit und Hilfe zum Gelingen
dieser Diplomarbeit beigetragen haben:
Prof. Dr. B. Hillebrands für die interessante Aufgabenstellung und die wissenschaftliche Betreuung.
Prof. Dr. M. Fleischhauer für die Übernahme des zweiten Gutachtens.
Dr. Oleksandre Serha für die Einführung in die Thematik, die hervorragende Zusammenarbeit und exzellente Betreuung.
Dr. Mikhail Kostylev für die Unterstützung bei allen theoretischen Problemen und
die hilfreichen und interessanten Diskussionen.
Christian Bayer für die Hilfe bei allen Problemen mit der BLS.
Dr. Britta Leven für die gute Unterstützung und Betreuung.
Bernd Pfaff und Dieter Weller für die Unterstützung bei technischen Fragen.
Eva-Maria Graefe, Sebastian Hermsdörfer und Thorsten Wagner für das unermüdliche Korrekturlesen.
Allen nicht namentlich erwähnten Mitgliedern der Arbeitsgruppe für die angenehme Zusammenarbeit und Hilfsbereitschaft.
Meinen Eltern für die Unterstützung vor und während meines Studiums.
71