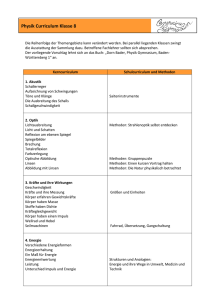
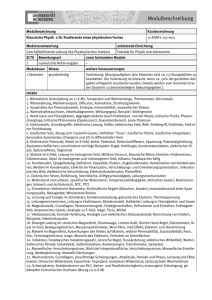
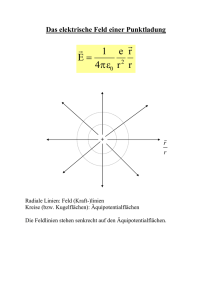
: q F E о о = r r r q E о о ⋅ ⋅ = 4 1

4.3 Elektrisches Feld
4.3.1
Definition, Feldlinien
Feld E wird definiert über die Kraftwirkung des Feldes auf eine
r
r
(bel.) positive Einheitsladung q:
→
FC = q2 ⋅ E
r
r FC
E :=
q2
Für eine Punktladung ergibt sich mit dem Coulombgesetz:
r
E=
r
q r
⋅ ⋅
4πε 0 r 2 r
1
• Die Kraftwirkung des E-Feldes auf eine pos. Probeladung verläuft tangential
entlang der Feldlinien.
• Die Dichte der Feldlinien beschreibt die rel. Stärke des (lokalen) E-Feldes
Superpositionsprinzip:
Elektromagnetische Felder (bzw. deren Wirkung)
überlagern sich ohne gegenseitige Störung.
Aus dem Superpositionsprinzip und der Symmetrie ergibt sich folgende
(homogene) Feldverteilung in einem Plattenkondensator:
Physik 4+2
Hoeppe, 2011
- 55 -
4.3.2
Elektrisches Potential
Das elektrisches Potential ϕ entspricht der potentiellen Energie einer
positiven Einheitsladung im elektrischen Feld:
E pot = ϕ ⋅ q
→
ϕ=
E pot
q
Als Elektrische Spannung U bezeichnet man die Differenz zweier Potentiale:
U ab := ∆ϕ = ϕ b − ϕ a
[U]=V
Volt
U·q entspricht also Energie: 1V · e = 1 eV = 1,602 ·10-19 C·V = 1,602 ·10-19 J
Der Zusammenhang von E-Feld bzw. Kraft und dem zugehörigen Potential
ergibt sich aus ‚Arbeit = Kraft x Weg’ :
dE pot
r r
r r
= q ⋅ dϕ = − F ⋅ dr = − q ⋅ E ⋅ dr
→
r r
dϕ = − E ⋅ dr
Integration liefert:
r r r
U ab = ∆ϕ = − ∫ E ( r ) dr
b
a
(wobei üblicherweise ϕ (∞) = 0 gesetzt wird)
Bsp.: Bewege Elektron durch das gesamte homogene Feld eines
Plattenkondensators auf die negative Seite:
Physik 4+2
Hoeppe, 2011
- 56 -
Aus dW = Fds folgt mit dEpot = -dW nach Integration für die Änderung
der potentiellen Energie des Elektrons:
∆E pot , e −
d
d
r r
r r
= − ∆W = − ∫ dW = − ∫ F ⋅ dx = − ∫ qE ⋅ dx = − ∫ − eE ⋅ dx = eE ⋅ d
b
d
a
0
0
0
Alternativ ergibt sich die Energieänderung aus der Potentialdifferenz zu:
xb
xb
r r r
= ∆ϕ = − ∫ E (r ) ⋅dr = − ∫ E ⋅ dx = − E ⋅ ∫ dx = − E ( xb − xa ) = − E ⋅ d
b
U ab
a
→
xa
xa
∆E pot , e − = q ⋅ ∆ϕ = −e ⋅ (− E ⋅ d ) = eE ⋅ d
Wird entsprechend Konvention U für positiven Pol positiv gewählt,
ergibt sich für das E-Feld im Plattenkondensator:
E=
4.3.3*
U
d
Feld als Gradient des Potentials
Die skalare Größe des Potentials, die Spannung, ist leicht zu messen,
einzustellen oder vorzugeben. Oft ist das Potential für ein Problem
auch einfacher zu berechnen. Das entsprechende E-Feld erhält man
einfach durch Differentiation:
bisher:
jetzt:
r r
dϕ = − E ⋅ d r
r
dϕ
E = − r = − grad ϕ = −∇ ϕ
dr
Gradient bzw. Nabla-Operator ∇:
⎛ ∂
grad ϕ = ∇ϕ = ⎜⎜ ,
⎝ ∂x
Physik 4+2
Hoeppe, 2011
∂
,
∂y
∂ ⎞
⎟
∂z ⎟⎠
- 57 -
4.3.4
Gaußscher Satz des elektrischen Feldes
Aus der ‚Zahl von Feldlinien’ die durch eine
geschlossene Oberfläche dringen, läßt sich
auf die Ladung innerhalb des entsprechenden
Volumens schließen:
Der elektrische Fluß durch eine beliebig geformte
geschlossene Oberfläche entspricht der darin
enthaltenen gesamten Ladung Q.
→ Gaußscher Satz:
r r
∫ ε 0 E ⋅ dA = Q
A
Unter Ausnutzung vorliegender Symmetrien lassen sich mit Hilfe des Gaußschen
Satzes Feldverteilungen berechnen:
Bsp.: Kugeloberfläche mit Punktladung im Zentrum:
r r
ε
E
∫ 0 ⋅ dA =
A
2π
π
∫ϕ ϑ∫ ε
0
E ⋅ r 2 sin ϑ dϑ dϕ =
=0 =0
π
= 2π r ε 0 E ∫ sin ϑ dϑ = 2π r 2ε 0 E ⋅ [− cos ϑ ] π0 = 4π r 2ε 0 E = Q
2
ϑ =0
Eine Ladung q im Zentrum der betrachteten Kugel →
E=
Physik 4+2
Hoeppe, 2011
q
4πε 0 r 2
d.h. Coulombgesetz folgt aus Gaußschem Satz!
- 58 -
Der Gaußsche Satz gilt für bel. Ladungsverteilungen, mit
Raumladungsdichte:
Flächenladungsdichte:
gilt
ρ (r ) =
r
dQ
dV
r
dQ
dA
σ (r ) =
oder der
r r
r
ε
E
⋅
d
A
=
ρ
(
r
∫ 0
∫ )dV
A
V
Ladungen auf elektrischen Leitern:
- Ladungen sammeln sich aufgrund der Coulombkräfte an der Oberfläche
- Bei (perfekten) Leitern sind alle Teile innerhalb des Leiters auf gleichem
Potential.
→ mit U = ∆ϕ = 0 folgt auch E = 0 innerhalb des Leiters.
→ Aus dem gleichen Grund bildet die Oberfläche eine Äquipotentialfläche,
die Tangentialkomponente verschwindet, d.h.
E steht senkrecht auf der Oberfläche.
Aus der Anwendung des Gaußschen Satzes auf ein Flächenelement ∆A mit der
Ladung ∆Q und E=0 innerhalb des Leiters folgt:
r
r
∫ ε 0 E ⋅ dA = ε 0 E ⋅ ∆A = ∆Q
∆A
ε0E = σ
→ Bsp.1: Ladung auf Metallkugel mit Radius R
→ Bsp.2: Ladung auf bel. geformten Metallkörpern
Physik 4+2
Hoeppe, 2011
- 59 -