Abiturvorbereitung Aufgabe 4 - klaus

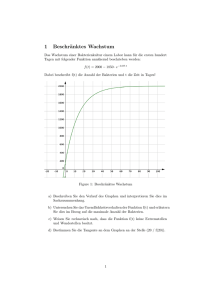
R. Brinkmann http://brinkmann-du.de
Seite 1
06.06.2017
Abiturvorbereitung Aufgabe 4
In einem Laborversuch soll die Entwicklung einer Bakterienkultur mit folgender
Exponentialfunktion modelliert werden:
f  x   n0  a  x  ek x
x  Zeit in Stunden, f  x   Anzahl der Bakterien
a) Bestimmen Sie geeignete Werte für n0, a und k, wenn die Anzahl der Bakterien
bei Versuchsbeginn 4 Millionen beträgt und nach x = 8 Stunden auf maximal 12
Millionen angewachsen ist. Stellen Sie die Funktionsgleichung auf.
(Kontrollergebnis: f  x  
1
 x
8
4  exe
)
b) Zeichnen Sie den Graphen in ein geeignetes Koordinatensystem. (I = [ 0 ; 52 ]).
Stellen Sie dazu eine Wertetabelle auf. Schrittweite 4, also x = 0, 4, 8, ..., 48, 52
c) Beschreiben Sie mit Worten den Entwicklungsverlauf der Bakterienkultur.
d) Berechnen Sie den Wendepunkt und überprüfen Sie diesen mit der 3. Ableitung.
Interpretieren Sie das Ergebnis in Bezug auf den Laborversuch.
e) Berechnen Sie die Fläche zwischen dem Graphen und der x- Achse im Intervall
[ 0 , 8 ]. Welche Bedeutung könnte die Fläche (Anzahl der Bakterien mal Zeit)
in Zusammenhang mit dem Laborversuch haben?
Kontrollergebnis:
 f  x  dx  4x  8  e  x  8   e
1
 x
8
f) Bestimmen Sie die Asymptote für f(x). Von welcher Bedeutung ist diese für den
Laborversuch?
Hilfestellung : lim x  ek  x  0 für k  0
x 
Erstellt von R. Brinkmann 841117876
02.02.2007 09:51:00
1 von 1