Selbstdiagnose zum Thema Rationale Zahlen

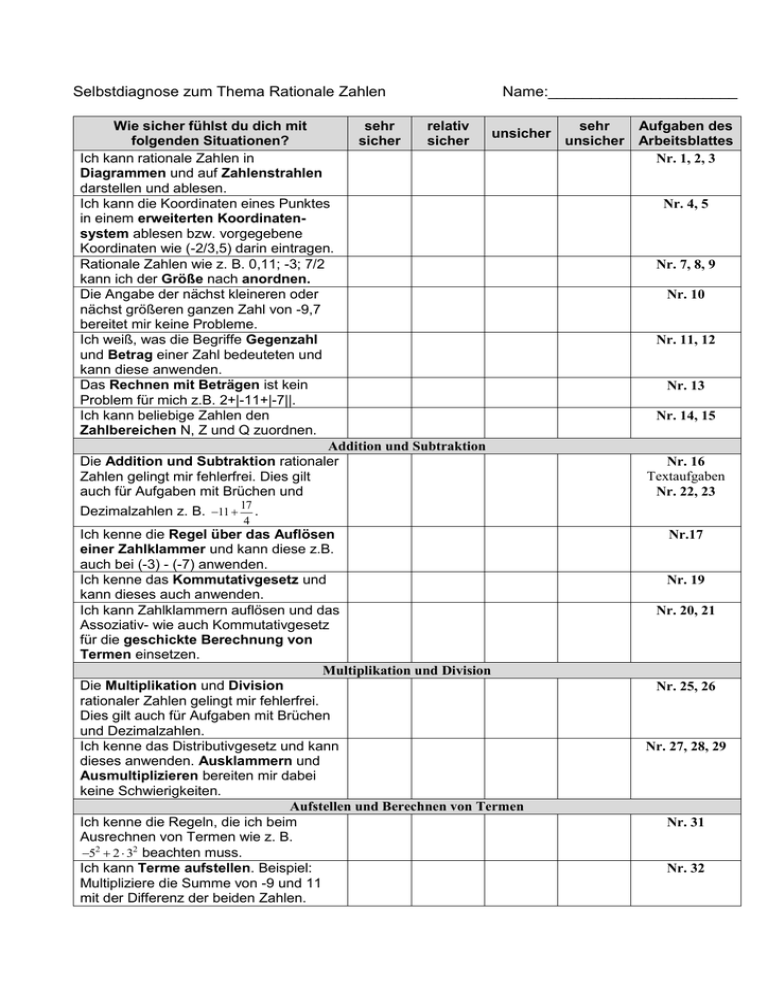
Selbstdiagnose zum Thema Rationale Zahlen
Name:______________________
Wie sicher fühlst du dich mit
sehr
relativ
sehr
unsicher
folgenden Situationen?
sicher
sicher
unsicher
Ich kann rationale Zahlen in
Diagrammen und auf Zahlenstrahlen
darstellen und ablesen.
Ich kann die Koordinaten eines Punktes
in einem erweiterten Koordinatensystem ablesen bzw. vorgegebene
Koordinaten wie (-2/3,5) darin eintragen.
Rationale Zahlen wie z. B. 0,11; -3; 7/2
kann ich der Größe nach anordnen.
Die Angabe der nächst kleineren oder
nächst größeren ganzen Zahl von -9,7
bereitet mir keine Probleme.
Ich weiß, was die Begriffe Gegenzahl
und Betrag einer Zahl bedeuteten und
kann diese anwenden.
Das Rechnen mit Beträgen ist kein
Problem für mich z.B. 2+|-11+|-7||.
Ich kann beliebige Zahlen den
Zahlbereichen N, Z und Q zuordnen.
Addition und Subtraktion
Die Addition und Subtraktion rationaler
Zahlen gelingt mir fehlerfrei. Dies gilt
auch für Aufgaben mit Brüchen und
Dezimalzahlen z. B. 11 

Aufgaben des
Arbeitsblattes
Nr. 1, 2, 3
Nr. 4, 5
Nr. 7, 8, 9
Nr. 10
Nr. 11, 12
Nr. 13
Nr. 14, 15
Nr. 16
Textaufgaben
Nr. 22, 23
17
.
4
Ich kenne die Regel über das Auflösen
einer Zahlklammer und kann diese z.B.
auch bei (-3) 
- (-7) anwenden.
Ich kenne das Kommutativgesetz und
kann dieses auch anwenden.
Ich kann Zahlklammern auflösen und das
Assoziativ- wie auch Kommutativgesetz
für die geschickte Berechnung von
Termen einsetzen.
Multiplikation und Division
Die Multiplikation und Division
rationaler Zahlen gelingt mir fehlerfrei.
Dies gilt auch für Aufgaben mit Brüchen
und Dezimalzahlen.
Ich kenne das Distributivgesetz und kann
dieses anwenden. Ausklammern und
Ausmultiplizieren bereiten mir dabei
keine Schwierigkeiten.
Aufstellen und Berechnen von Termen
Ich kenne die Regeln, die ich beim
Ausrechnen von Termen wie z. B.
52  2  32 beachten muss.
Ich kann Terme aufstellen. Beispiel:
Multipliziere die Summe von -9 und 11
mit der Differenz der beiden Zahlen.
Nr.17
Nr. 19
Nr. 20, 21
Nr. 25, 26
Nr. 27, 28, 29
Nr. 31
Nr. 32