3. Schriftliche Wiederholung aus Physik Donnerstag, 27. Februar 1997

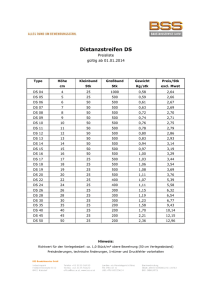
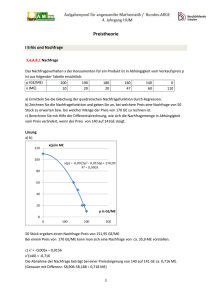
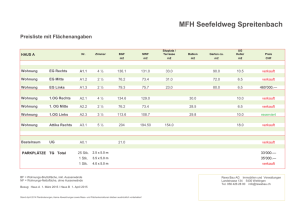
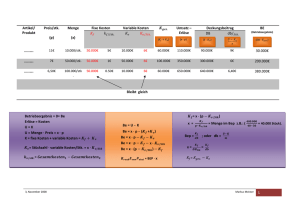
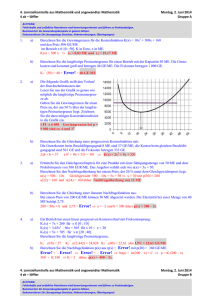
3. Schularbeit aus Mathematik
4 ck - menschik
1. a)
Dienstag, 15. Mai 2007
Gruppe A
Ausführung
Ein Produkt hat konstante Grenzkosten von 40 €/Stk. und Fixkosten von 360.000 €. Die Kapazität beträgt
20.000 Stk.. Wo liegt das Betriebsoptimum und die langfristige Preisuntergrenze. Welcher Preis muss verlangt
werden, damit der Break-even bei 30 % Beschäftigungsgrad auftritt?
K(x) = 40x + 360.000 für x  [0 / 20.000]. Betriebsoptimum ist der rechte Randpunkt BO = 20.000 und die
LPU = Error! = 40 + 18 = 58 €/Stk. = LPU
p · 6.000 = 40 · 6.000 + 360.000  p = 100 €/Stk.
b)
Ein Betrieb hat eine Kostenfunktion von K(x) = 10x2 + 300x + 49.000 für x  [0 ME / 150 ME]. Berechnen
Sie die langfristige Preisuntergrenze. Wie hoch muss der Verkaufspreis sein, wenn er um 60 % über der
langfristigen Preisuntergrenze liegen soll?
–
K; (x) = 10x + 300 + Error! Error! = 10 – Error! = 0  x = BO = 70
GE/ME  p = 1,6 · 1.700 = 2.720 GE/ME
c)
Error!(70) = LPU = 1.700
Berechnen Sie den maximalen Gewinn für die Kostenfunktion K(x) = 10x2 + 300x + 49.000 und den
konstanten Marktpreis 2.700 GE/ME.
K’ = E’  20x + 300 = 2.700  20x = 2.400  x = 120
G(120) = 120 · 2.700 – 229.000 GE = 95.000 GE = Gmax
2. a)
Berechnen Sie die Gleichung einer S-förmigen Kostenkurve aus:
Die Kosten beim Beschäftigungsgrad 4 ME sind 6.240 GE, beim BG 10 ME sind sie 10.800 GE. Die
minimalen Grenzkosten sind 724 GE/ME und treten beim BG 8 ME auf.
K(x) = ax3 + bx2 + cx + d
K(4) = 6240 = 64a + 16b + 4c + d K(10) = 10.800 = 1000a + 100b + 10c + d
K“(8) = 6 · a · 64 + 2 · b = 0 und K’(8) = 3 a 64 + 2b · 8 + c  a = 3 b = –72 c = 1.300 d = 2.000
b)
Berechnen Sie die Gewinngrenzen und den maximalen Gewinn für
K(x) = 3x3 – 70x2 + 1.400x + 1.500 und p(x) = 3000 – 150x.
G(x) = p(x) · x – K(x) G’(x) = –9x2 – 160x + 1.600 = 0  xgmax = 7,14
G(7,14) = 4.753,7 Gewinngrenzen G(x) = 0  x1 = 0,99 ME und x2 = 12,6 ME
3 a)
Eine Nachfragefunktion hat die Form p(x) = Error!. Ermitteln Sie die Parameter a, b und c aus: Bei einem
Preis von 7,5 GE/ME können 10 ME verkauft werden. Senkt man den Preis um 2,5 GE/ME, dann können um
50 % mehr verkauft werden. Die Sättigungsmenge beträgt 40 ME.
7,5 (10 + c) = 10a + b
p(x) = Error!
b)
5(15 + c) = 15a + b
Maximum bei E’(x) = 0  x = 14,5 ME E(14,5) = 126
Eine Nachfragefunktion lautet p(x) = 300 – 0,2x. Welche Menge wird bei einem Preisniveau von 100 GE/ME
verkauft. Um welchen Prozentsatz ist der Preis für eine Absatzsteigerung von 20 % zu senken?
100 = 300 – 0,2x  x = 1.000
A
und 0 = 40a + b  a = –5 b = 200 c = 10
Berechnen Sie den maximalen Erlös für p(x) = Error!.
E(x) = p(x) · x
c)
und
p(1.200) = 300 – 0,2 · 1.200 = 60 also um 40 % weniger
4. a)
Konstruieren Sie den Cournotpunkt aus folgenden Bestimmungsstücken:
die Grenzkosten verlaufen linear und betragen für 80 ME 26 GE/ME. Wird der Beschäftigungsgrad um 25 %
gesenkt ,dann sinken die Grenzkosten um 4 GE/ME. Die Nachfragefunktion ist linear mit einer
Sättigungsmenge von 200 ME. Bei einem Verkaufspreis von 10 GE/ME können 150 ME abgesetzt werden.
Wie hoch ist der Prohibitivpreis?
60
Maßstab:
x:
1 : 20
50
y:
1:5
C (50 / 30) Prohibitivpreis = 40 GE/ME
K'
40
30
20
p
E'
10
0
0
100
150
200
250
In der Grafik sind die Durchschnittskosten Kd, die konstante Preisfunktion p und die lineare
Grenzkostenfunktion K’ eingezeichnet. Ermitteln Sie aus der Grafik:
den Gewinnbereich,
die langfristige Preisuntergrenze,
den maximalen Gewinn!
Gewinnbereich:
Schnittpunkte p mit Kd

x  [20.000 Stk. /
70.000 Stk.]
in 100 €/Stk.
b)
50
12
11
10
9
langfristige
Preisuntergrenze =
minimales Kd = 500
€/Stk.
8
Stelle des maximalen
Gewinns = Schnittpunkt
von E’ = p mit K’ 
47.000 Stk, multipliziert
mit dem Stückgewinn =
p – Kd = 600 – 510 = 90
ergibt Gmax = 90 ·
47.000  4,3 Mio. €
5
Kd
7
p
6
4
3
K'
2
1
0
0
10
20
30
40
50
60
70
80
Beschäftigungsgrad in 1.000 Stk.
90
100
110
3. Schularbeit aus Mathematik
4 ck - menschik
1. a)
Dienstag, 15. Mai 2007
Gruppe B
Ausführung
Ein Produkt hat konstante Grenzkosten von 20 €/Stk. und Fixkosten von 180.000 €. Die Kapazität beträgt
20.000 Stk.. Wo liegt das Betriebsoptimum und die langfristige Preisuntergrenze. Welcher Preis muss verlangt
werden, damit der Break-even bei 30 % Beschäftigungsgrad auftritt?
K(x) = 20x + 180.000 für x  [0 / 20.000]. Betriebsoptimum ist der rechte Randpunkt BO = 20.000 und die
LPU = Error! = 20 + 9 = 29 €/Stk. = LPU
p · 6.000 = 20 · 6.000 + 180.000  p = 50 €/Stk.
b)
Ein Betrieb hat eine Kostenfunktion von K(x) = 10x2 + 300x + 64.000 für x  [0 ME / 150 ME]. Berechnen
Sie die langfristige Preisuntergrenze. Wie hoch muss der Verkaufspreis sein, wenn er um 60 % über der
langfristigen Preisuntergrenze liegen soll?
–
K; (x) = 10x + 300 + Error! Error! = 10 – Error! = 0  x = BO = 80
GE/ME  p = 1,6 · 1.900 = 3.040 GE/ME
c)
Error!(80) = LPU = 1.900
Berechnen Sie den maximalen Gewinn für die Kostenfunktion K(x) = 10x2 + 300x + 64.000 und den
konstanten Marktpreis 2.700 GE/ME.
K’ = E’  20x + 300 = 2.700  20x = 2.400  x = 120
G(120) = 120 · 2.700 – 244.000 GE = 80.000 GE = Gmax
2. a)
Berechnen Sie die Gleichung einer S-förmigen Kostenkurve aus:
Die Kosten beim Beschäftigungsgrad 4 ME sind 6.240 GE, beim BG 10 ME sind sie 10.800 GE. Die
minimalen Grenzkosten sind 724 GE/ME und treten beim BG 8 ME auf.
K(x) = ax3 + bx2 + cx + d
K(4) = 6240 = 64a + 16b + 4c + d K(10) = 10.800 = 1000a + 100b + 10c + d
K“(8) = 6 · a · 64 + 2 · b = 0 und K’(8) = 3 a 64 + 2b · 8 + c  a = 3 b = –72 c = 1.300 d = 2.000
b)
Berechnen Sie die Gewinngrenzen und den maximalen Gewinn für
K(x) = 3x3 – 70x2 + 1.400x + 1.500 und p(x) = 3000 – 150x.
G(x) = p(x) · x – K(x) G’(x) = –9x2 – 160x + 1.600 = 0  xgmax = 7,14
G(7,14) = 4.753,7 Gewinngrenzen G(x) = 0  x1 = 0,99 ME und x2 = 12,6 ME
3 a)
Eine Nachfragefunktion hat die Form p(x) = Error!. Ermitteln Sie die Parameter a, b und c aus: Bei einem
Preis von 7,5 GE/ME können 10 ME verkauft werden. Senkt man den Preis um 2,5 GE/ME, dann können um
50 % mehr verkauft werden. Die Sättigungsmenge beträgt 40 ME.
7,5 (10 + c) = 10a + b
p(x) = Error!
b)
5(15 + c) = 15a + b
Maximum bei E’(x) = 0  x = 14,5 ME E(14,5) = 126
Eine Nachfragefunktion lautet p(x) = 300 – 0,2x. Welche Menge wird bei einem Preisniveau von 100 GE/ME
verkauft. Um welchen Prozentsatz ist der Preis für eine Absatzsteigerung von 20 % zu senken?
100 = 300 – 0,2x  x = 1.000
B
und 0 = 40a + b  a = –5 b = 200 c = 10
Berechnen Sie den maximalen Erlös für p(x) = Error!.
E(x) = p(x) · x
c)
und
p(1.200) = 300 – 0,2 · 1.200 = 60 also um 40 % weniger
4. a)
Konstruieren Sie den Cournotpunkt aus folgenden
Bestimmungsstücken:
die Grenzkosten verlaufen linear und betragen für
80 ME 58 GE/ME. Wird der Beschäftigungsgrad
um 25 % gesenkt ,dann sinken die Grenzkosten
um 12 GE/ME. Die Nachfragefunktion ist linear
mit einer Sättigungsmenge von 200 ME. Bei
einem Verkaufspreis von 20 GE/ME können 150
ME abgesetzt werden.
Wie hoch ist der Prohibitivpreis?
Maßstab:
x:
1 : 20
y:
1 : 10
C (50 / 30) Prohibitivpreis = 80 GE/ME
140
120
100
K'
80
60
40
p
E'
20
0
b)
In der Grafik sind die
Durchschnittskosten Kd, die
konstante Preisfunktion p und die
lineare Grenzkostenfunktion K’
eingezeichnet. Ermitteln Sie aus
der Grafik:
den Gewinnbereich,
die langfristige Preisuntergrenze,
den maximalen Gewinn!
in 100 €/Stk.
0
50
150
200
250
12
11
10
9
8
Kd
7
Gewinnbereich:
Schnittpunkte p mit Kd 
x  [16.000 Stk. / 80.000 Stk.]
100
p
6
5
4
langfristige Preisuntergrenze =
minimales Kd = 500 €/Stk.
3
Stelle des maximalen Gewinns =
Schnittpunkt von E’ = p mit K’ 
57.000 Stk, multipliziert mit dem
Stückgewinn = p – Kd = 700 –
540 = 160 ergibt Gmax = 160 ·
57.000  9 Mio. €
1
K'
2
0
0
10
20
30
40
50
60
70
80
Beschäftigungsgrad in 1.000 Stk.
90
100
110
3. Schularbeit aus Mathematik
4 ck - menschik
1. a)
Dienstag, 15. Mai 2007
Gruppe A
Ein Produkt hat konstante Grenzkosten von 40 €/Stk. und Fixkosten von 360.000 €. Die Kapazität beträgt
20.000 Stk.. Wo liegt das Betriebsoptimum und die langfristige Preisuntergrenze. Welcher Preis muss verlangt
werden, damit der Break-even bei 30 % Beschäftigungsgrad auftritt?
b)
Ein Betrieb hat eine Kostenfunktion von K(x) = 10x2 + 300x + 49.000 für x  [0 ME / 150 ME]. Berechnen
Sie die langfristige Preisuntergrenze. Wie hoch muss der Verkaufspreis sein, wenn er um 60 % über der
langfristigen Preisuntergrenze liegen soll?
c)
Berechnen Sie den maximalen Gewinn für die Kostenfunktion K(x) = 10x2 + 300x + 49.000 und den
konstanten Marktpreis 2.700 GE/ME.
2. a)
Berechnen Sie die Gleichung einer S-förmigen Kostenkurve aus:
Die Kosten beim Beschäftigungsgrad 4 ME sind 6.240 GE, beim BG 10 ME sind sie 10.800 GE. Die
minimalen Grenzkosten sind 724 GE/ME und treten beim BG 8 ME auf.
b)
3 a)
Berechnen Sie die Gewinngrenzen und den maximalen Gewinn für
K(x) = 3x3 – 70x2 + 1.400x + 1.500 und p(x) = 3000 – 150x.
Eine Nachfragefunktion hat die Form p(x) = Error!. Ermitteln Sie die Parameter a, b und c aus: Bei einem
Preis von 7,5 GE/ME können 10 ME verkauft werden. Senkt man den Preis um 2,5 GE/ME, dann können um
50 % mehr verkauft werden. Die Sättigungsmenge beträgt 40 ME.
b)
Berechnen Sie den maximalen Erlös für p(x) = Error!.
c)
Eine Nachfragefunktion lautet p(x) = 300 – 0,2x. Welche Menge wird bei einem Preisniveau von 100 GE/ME
verkauft. Um welchen Prozentsatz ist der Preis für eine Absatzsteigerung von 20 % zu senken?
b)
Konstruieren Sie den Cournotpunkt aus folgenden Bestimmungsstücken:
die Grenzkosten verlaufen linear und betragen für 80 ME 26 GE/ME. Wird der Beschäftigungsgrad um 25 %
gesenkt ,dann sinken die Grenzkosten um 4 GE/ME. Die Nachfragefunktion ist linear mit einer
Sättigungsmenge von 200 ME. Bei einem Verkaufspreis von 10 GE/ME können 150 ME abgesetzt werden.
Wie hoch ist der Prohibitivpreis?
Maßstab:
x:
1 : 20
y:
1:5
In der Grafik sind die
Durchschnittskosten Kd,
die konstante Preisfunktion p
und die lineare Grenzkostenfunktion K’
eingezeichnet.
Ermitteln Sie aus der Grafik:
den Gewinnbereich,
die langfristige Preisuntergrenze,
den maximalen Gewinn!
in 100 €/Stk.
4. a)
12
11
10
9
8
Kd
7
p
6
5
4
3
K'
2
1
0
0
10
20
30
40
50
60
70
80
Beschäftigungsgrad in 1.000 Stk.
90
100
110
3. Schularbeit aus Mathematik
4 ck - menschik
1. a)
Dienstag, 15. Mai 2007
Gruppe B
Ein Produkt hat konstante Grenzkosten von 20 €/Stk. und Fixkosten von 180.000 €. Die Kapazität beträgt
20.000 Stk.. Wo liegt das Betriebsoptimum und die langfristige Preisuntergrenze. Welcher Preis muss verlangt
werden, damit der Break-even bei 30 % Beschäftigungsgrad auftritt?
b)
Ein Betrieb hat eine Kostenfunktion von K(x) = 10x2 + 300x + 64.000 für x  [0 ME / 150 ME]. Berechnen
Sie die langfristige Preisuntergrenze. Wie hoch muss der Verkaufspreis sein, wenn er um 60 % über der
langfristigen Preisuntergrenze liegen soll?
c)
Berechnen Sie den maximalen Gewinn für die Kostenfunktion K(x) = 10x2 + 300x + 64.000 und den
konstanten Marktpreis 2.700 GE/ME.
2. a)
Berechnen Sie die Gleichung einer S-förmigen Kostenkurve aus:
Die Kosten beim Beschäftigungsgrad 4 ME sind 6.240 GE, beim BG 10 ME sind sie 10.800 GE. Die
minimalen Grenzkosten sind 724 GE/ME und treten beim BG 8 ME auf.
b)
3 a)
b)
c)
Berechnen Sie die Gewinngrenzen und den maximalen Gewinn für
K(x) = 3x3 – 70x2 + 1.400x + 1.500 und p(x) = 3000 – 150x.
Eine Nachfragefunktion hat die Form p(x) = Error!. Ermitteln Sie die Parameter a, b und c aus: Bei einem
Preis von 7,5 GE/ME können 10 ME verkauft werden. Senkt man den Preis um 2,5 GE/ME, dann können um
50 % mehr verkauft werden. Die Sättigungsmenge beträgt 40 ME.
Berechnen Sie den maximalen Erlös für p(x) = Error!.
Eine Nachfragefunktion lautet p(x) = 300 – 0,2x. Welche Menge wird bei einem Preisniveau von 100 GE/ME
verkauft. Um welchen Prozentsatz ist der Preis für eine Absatzsteigerung von 20 % zu senken?
Konstruieren Sie den Cournotpunkt aus folgenden Bestimmungsstücken:
die Grenzkosten verlaufen linear und betragen für 80 ME 58 GE/ME. Wird der Beschäftigungsgrad um 25 %
gesenkt ,dann sinken die Grenzkosten um 12 GE/ME. Die Nachfragefunktion ist linear mit einer
Sättigungsmenge von 200 ME. Bei einem Verkaufspreis von 20 GE/ME können 150 ME abgesetzt werden.
Wie hoch ist der Prohibitivpreis?
Maßstab:
x:
1 : 20
12
y:
1 : 10
b)
In der Grafik sind
die Durchschnittskosten Kd,
die konstante Preisfunktion p
und die lineare Grenzkostenfunktion K’
eingezeichnet.
Ermitteln Sie aus der Grafik:
den Gewinnbereich,
die langfristige Preisuntergrenze,
den maximalen Gewinn!
in 100 €/Stk.
4. a)
11
10
9
8
Kd
7
p
6
5
4
3
K'
2
1
0
0
10
20
30
40
50
60
70
80
Beschäftigungsgrad in 1.000 Stk.
90
100
110