Aufgaben

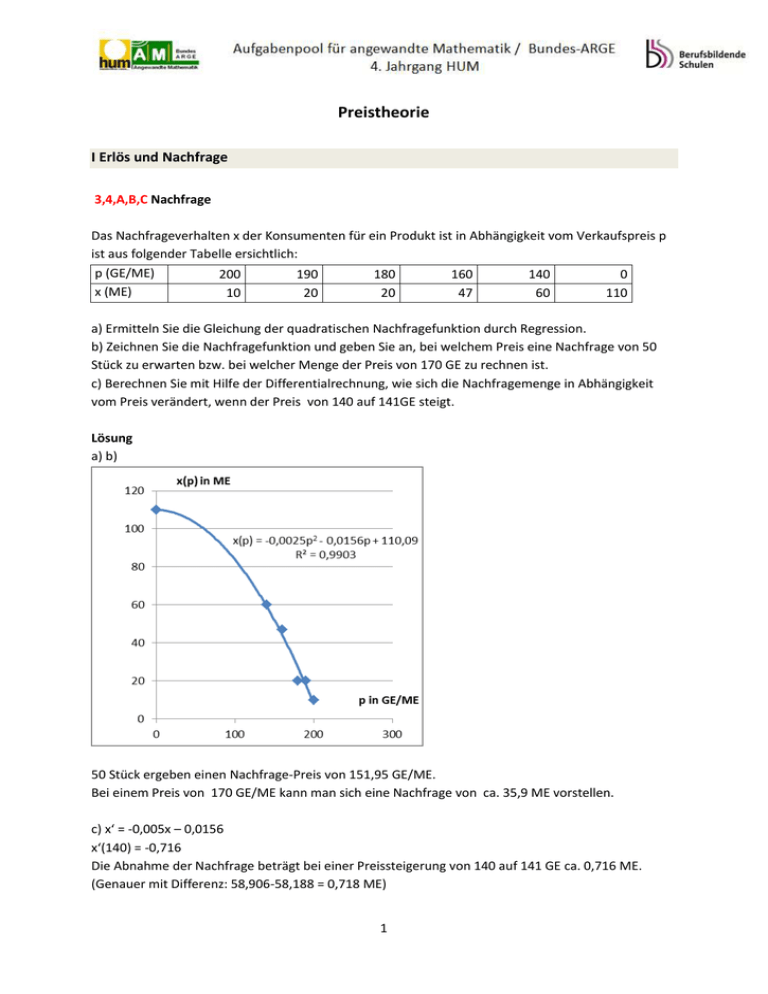
Preistheorie
I Erlös und Nachfrage
3,4,A,B,C Nachfrage
Das Nachfrageverhalten x der Konsumenten für ein Produkt ist in Abhängigkeit vom Verkaufspreis p
ist aus folgender Tabelle ersichtlich:
p (GE/ME)
200
190
180
160
140
0
x (ME)
10
20
20
47
60
110
a) Ermitteln Sie die Gleichung der quadratischen Nachfragefunktion durch Regression.
b) Zeichnen Sie die Nachfragefunktion und geben Sie an, bei welchem Preis eine Nachfrage von 50
Stück zu erwarten bzw. bei welcher Menge der Preis von 170 GE zu rechnen ist.
c) Berechnen Sie mit Hilfe der Differentialrechnung, wie sich die Nachfragemenge in Abhängigkeit
vom Preis verändert, wenn der Preis von 140 auf 141GE steigt.
Lösung
a) b)
50 Stück ergeben einen Nachfrage-Preis von 151,95 GE/ME.
Bei einem Preis von 170 GE/ME kann man sich eine Nachfrage von ca. 35,9 ME vorstellen.
c) x‘ = -0,005x – 0,0156
x‘(140) = -0,716
Die Abnahme der Nachfrage beträgt bei einer Preissteigerung von 140 auf 141 GE ca. 0,716 ME.
(Genauer mit Differenz: 58,906-58,188 = 0,718 ME)
1
3,4 A,B,C,D Nachfragefunktion
Bei der Produktion eines Produkts wird das Nachfrageverhalten der Konsumenten ermittelt:
P (GE/ME)
140
160
180
190
200
x (ME)
70
55
34
22
10
a) Ermitteln Sie die Gleichung einer quadratischen Nachfragefunktion, die die gegebenen Wertepaare
möglichst gut beschreibt!
b) Ermitteln Sie grafisch, bei welchem Preis eine Nachfrage von 50 ME erwartet werden kann.
c) Berechnen Sie, welche Nachfrage bei einem Preis von 170 GE zu erwarten ist.
d) Erklären Sie, wie mit Hilfe der Differentialrechnung die Änderung des Nachfrageverhaltens bei
einer Erhöhung des Preises um 1 GE ermittelt werden kann.
e) Berechnen und interpretieren Sie aus der Nachfragefunktion x(p) den Höchstpreis und die
Sättigungsmenge.
Lösung
a) b)c)
Eine Nachfrage von 50 ME kann man bei einem Preisangebot von 166,21 GE/ME erwarten und bei
170 GE/ME ist mit einer Nachfrage von 46,32 ME zu rechnen.
d) Durch Ableiten von x(p) und Einsetzen des Preises po - also: x‘(p0) - erhält man die Änderung der
Nachfrage bei Erhöhung des Preises von p0 auf p0+1.
e) Höchstpreis: p(0) = 208,45 GE, Nachfrage ist = 0, unverkäuflich, weil der Preis zu hoch ist
Sättigungsmenge x (0) = 56,21 ME, das Produkt ist uninteressant, der Markt ist gesättigt.
2
A,B,C,D CD-Player
Die Firma Schwarz und CO stellt Überlegungen zur Preisgestaltung des Artikels
„tragbarer CD-Player, Typ PL-234“ an:
Die Preisfunktion im Angebot wird ermittelt mit: p A  x  1
Die Preisfunktion bei der Nachfrage ergibt: p N   x  4
2
x…Menge, Mengeneinheit: 1 ME = 1 STK
p…Preis , wird in 100 €/Stk = 1GE/ STK angegeben
a) Berechnen Sie , welchen Verkaufspreis bei Ausbringung von 7 Stück der Produzent und welchen
Preis der Konsument erwartet.
b) Zeichnen Sie die Nachfragefunktion x (p) und lesen Sie den Höchstpreis und die Sättigungsmenge
ab.
c) Erklären Sie, wie Sie das Maximum des Verkaufserlöses berechnen können.
Lösung
a) Der Produzent erwartet bei 7 Stück einen Angebotspreis von 800 €/STK.
Der Konsument erwartet bei 7 Stück den Nachfragepreis von 50 €/STK.
b) Die Sättigungsmenge ist bei ungefähr 8 Stück, Höchst-Nachfragepreis ist 400 €/STK.
c) Erlös: E = pN ∙ x = -0,5x² + 4x
Man leitet E nach x ab und setzt die Gleichung = 0.
Daraus berechnet man x. Diesen Wert setzt man wieder in die Gleichung für den Erlös ein und erhält
so das Erlösmaximum.
3
II Gewinnanalyse
3,4 A,B,C Gewinn und Grenzbetrieb1 bei vollständiger Konkurrenz
Ein Betrieb hat bei der Herstellung eines Produkts die Kostenfunktion
K(x) = 0,001x³ - 0,1x² + 4x + 50 ermittelt.
a) Berechne für p = 3 GE/ME den maximalen Gewinn
b) Zeichne für p = 3 GE/ME die Gewinnfunktion und lies die Gewinnschwelle (break-even point) und
die Gewinngrenze ab.
c) Bestimme, welcher Verkaufspreis im Grenzbetrieb erzielt wird.
Grenzbetrieb heißt, es wird kein Gewinn gemacht, die Herstellungsmenge ist das Betriebsoptimum.
Lösung:
a) G(x) = p∙x – K = 3x- (0,001x³ - 0,1x² + 4x + 50)
G‘(x) = -0,003x² + 0,2x - 1 = 0 mit G‘‘(x) = -0,006x +0,2
x = 61 ME (die 2. Lösung 5 liefert kein Maximum)
Gmax = 34 GE.
b) Break even Point bei einem Absatz von ca. 37,5 ME, Gewinngrenze: ca. 79 ME
Genaue Ablesung der Gewinnzone zB mit Geogebra: 37,33 bis 79,52 ME.
c) p = k(xo) Stückkosten am Betriebsoptimum
k = K/x = 0,001x² - 0,1x +4 + 50/x, das Minimum mit TE  x0 = 57,55 ME
p = k(57,55) = 2,43 GE/ME
1
(Teile aus „Kosten- und Preistheorie“ , Skriptum von M. Bruckbauer 2005, Angabe verändert)
4
3,4, A,B,C Gewinn bei einem Monopolanbieter
Die Nachfrage x bei einem Monopolanbieter bestimmt den Preis.
p(x) = - 0,12x² -2x + 40 gegeben; p in GE/ME, x in ME.
Die Kostenfunktion für die Herstellung des Produkts lautet:
K(x) = 0,2x² + 2x +4; K in GE
a) Berechnen Sie mit Hilfe der Differentialrechnung das Erlösmaximum.
b) Zeichnen und diskutieren Sie die Gewinnfunktion in Bezug auf Nullstellen und Maximum.
c) Berechnen Sie den Cournot’schen Punkt mit Hilfe der Differentialrechnung
a) E = - 0,12x³ -2x² + 40x
E‘ = -0,36x² -4x + 40 = 0  x ≈ 6,36 ME
Emax = 142,63 GE
b) Der Break-even point liegt bei einem Absatz von ca. 0,1 ME, die Gewinngrenze befindet sich bei
ca. 10,8 ME. Das Gewinnmaximum beträgt ungefähr 119 GE bei einem Absatz von ca. 6 ME.
Genaue Ablesung z.B. mit Geogebra, Gewinnzone: x1 = 0,106 ME; x2 = 10,77 ME
Gewinnmaximum bei 5,84 ME beträgt 118,99 GE
c) Cournot’scher Punkt: ( xmax , p(xmax))
Das Gewinnmaximum mit Differenzialrechnung:
G(x) = - 0,12x³ -2x² + 40x –(0,2x² + 2x + 4) = -0,12x³ -2,2x² +38x -4
G‘ (x) = -0,36x² -4,4x + 38 = 0  xmax = 5,84 ME
p(xmax) = 24,4GE/ME
Cornot‘scher Punkt: ( 5,84|24,4) liegt auf der Absatz-Preisfunktion.
5