3.ÜSA 10.11.04

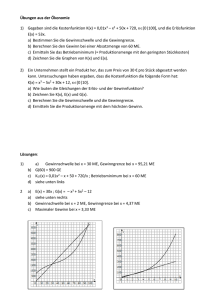
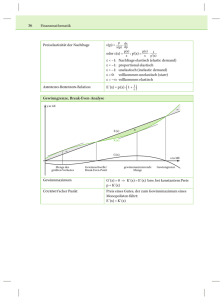
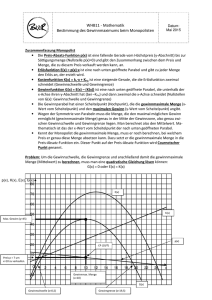
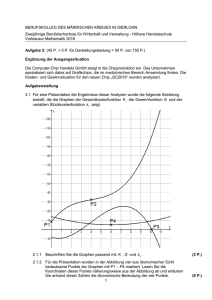
3. Übungsschularbeit, am 10. November 2004
 Diskutiere die Funktion f(x)! (Definitionsmenge, Pole, Lücken, Asymptote, Nullstellen,
Hoch-/Tiefpunkte, Wendepunkte mit Steigung)
Zeichne die Funktion im Intervall [-5;8]!
f(x) =
4x3  9x 2
4x 2 16x  16
(25 Punkte)
 Ermittle:
a) die gewinnmaximierende Menge und den zugehörigen Preis,
b) den maximalen Gewinn,
c) die erlösmaximierende Menge und den zugehörigen Preis,
d) den maximalen Erlös,
e) die Elastizität im COURNOTschen Punkt,
f) die Sättigungsmenge,
g) die Gewinnschwelle und die Gewinngrenze,
h) die Kostenkehre (Wo sind die Kosten progressiv, wo regressiv?) und
i) das Durchschnittskostenminimum samt kostendeckenden Preis
eines Monopolbetriebs, für den die Kostenfunktion K(x) und die Nachfragefunktion p(x)
gegeben sind!
K(x) = 0,01·x3 – 2·x2 + 300·x + 5760
p(x) = 1000 – 0,3·x
(25 Punkte)