Kosten – Erlös – Gewinn: Ganzrationale Funktionen in der

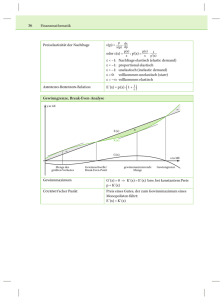
Kosten – Erlös – Gewinn (1)
Bei der Produktion von Gütern entstehen Kosten, durch den Verkauf wird Geld eingenommen und,
wenn alles gut läuft, Gewinn gemacht. Die Wirtschaftsmathematik versucht, unter Zuhilfenahme
von Modellen Kosten, Erlös und Gewinn durch Funktionen zu beschreiben und Zusammenhänge
sowie charakteristische Eigenschaften zu berechnen.
Bei der Produktion von Waren entstehen Kosten. Diese setzen sich zusammen aus den Fixkosten
und den variablen Kosten.
Die Fixkosten sind unabhängig von der produzierten Menge; sie fallen immer an, auch wenn nichts
hergestellt wird: z.B. _______________________________________________________________
Die variablen Kosten sind die produktionsbedingten Kosten; ihre Höhe hängt von der
Produktionsmenge ab: z.B. _________________________________________________________________
Die Kostenfunktion K(x) beschreibt die Kosten für die Produktion von x Mengeneinheiten eines
Produktes: K(x) = Kvar(x) + Kfix
Der Erlös ist das Geld, das durch den Verkauf der hergestellten Waren eingenommen wird. Der
Preis kann dabei konstant sein oder sich in Abhängigkeit von der Warenmenge verändern.
Die Preisfunktion p(x) gibt, wie viele Geldeinheiten eine produzierte Mengeneinheit kostet.
Die Erlösfunktion E(x) gibt an, wie viele Geldeinheiten durch den Verkauf von x Mengeneinheiten
zum Preis p(x) eingenommen werden: E(x) = p(x)x
Unter der Annahme, dass alle produzierten Güter auch verkauft werden, lässt sich Bilanz ziehen:
Bleibt nach dem Abzug der Kosten vom Erlös noch Geld übrig, so wurde Gewinn gemacht. Sind die
Kosten höher als der Erlös, macht das Unternehmen Verlust.
Die Übergänge zwischen Gewinn und Verlust nennt man Gewinnschwelle und Gewinngrenze.
Die Gewinnfunktion G(x) beschreibt den Gewinn durch Produktion und Verkauf von x
Mengeneinheiten: G(x) = E(x) – K(x). Ist G(x) positiv, macht das Unternehmen Gewinn, ist G(x)
negativ spricht man von Verlust.
Kosten – Erlös – Gewinn (2)
Ein Fertigungsbetrieb hat seine Produktionskosten in Abhängigkeit von der hergestellten Menge
untersucht und dabei folgende Daten ermittelt:
Die Fixkosten betragen 24 GE. Bei der Produktion von 1 ME ergeben sich Kosten von 35 GE, bei 3
ME sind die Kosten 45 GE, bei 4 ME betragen die Kosten 56 GE
( 1 ME (Mengeneinheit) = 1000 Stück , 1 GE (Geldeinheit) = 1000 € )
Das Unternehmen kann maximal 7 ME produzieren.
a) Tragen Sie die ermittelten Kosten in ein Koordinatensystem ein.
x-Achse: Produktionsmenge in ME, y-Achse: Kosten in GE
b) K(x) soll eine ganzrationale Funktion möglichst niedrigen Grades sein.
Bestimmen Sie die Gleichung der Kostenfunktion.
c) Wie hoch sind die Fixkosten und die variablen Kosten bei einer Produktion von 2 ME?
d) Bestimmen Sie mit Hilfe des Taschenrechners (MODE 7) weitere Funktionswerte und zeichnen
Sie die vollständige Kostenfunktion.
e) Die Erzeugnisse werden zu einem Preis von 20 GE pro Stück verkauft werden. Bestimmen Sie
die Gleichung der Erlösfunktion und zeichnen Sie diese in dasselbe Koordinatensystem.
f) Bestimmen Sie die Gleichung der Gewinnfunktion und zeichnen Sie diese in dasselbe
Koordinatensystem.
g) Bestimmen Sie die Gewinnschwelle und die Gewinngrenze. Geben Sie an, bei welchen
Produktionsmengen der Betrieb Gewinn und Verlust macht.
h) Bestimmen Sie mit Hilfe des Taschenrechners möglichst genau die Produktionsmenge, bei der
der Gewinn maximal ist.
Chip-Unternehmen
Ein Unternehmen stellt Mikrochips her, die zum Preis von 20 € je Stück abgesetzt werden können.
Untersuchungen haben die Kostenfunktion K(x) = x3 – 10x2 + 35x + 18 , x  [0|10] ergeben.
a)
b)
c)
d)
Bestimmen Sie die Gleichungen der Erlös- und der Gewinnfunktion.
Berechnen Sie die Gewinnschwelle und die Gewinngrenze.
Zeichnen Sie alle drei Funktionen in ein Koordinatensystem.
Bestimmen Sie die Stückkostenfunktion KSt und zeichnen Sie diese ebenfalls ein.
(KSt(x) beschreibt die Gesamtkosten K(x) pro Mengeneinheit x an.)
e) Welcher Punkt der Stückkostenkurve ist für das Unternehmen interessant? Wo liegt dieser
Punkt?
Lösungen
K(x) = x³ - 6x² + 16x + 24
E(x) = 20x
G(x) = E(x) – K(x) = - x³ + 6x² + 4x - 24
Gewinnschwelle bei 2 ME, Gewinngrenze bei 6 ME
Gmax(4,309|24,634)
E(x) = 20x
G(x) = - x3 + 10x2 - 15x - 18
Gewinnschwelle bei 3 ME
Gewinngrenze bei 7,77 ME
KST(x) = x2 – 10x + 35 + 18/x
Geringste Stückkosten bei 5,32 ME