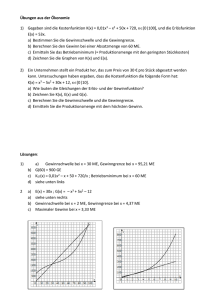
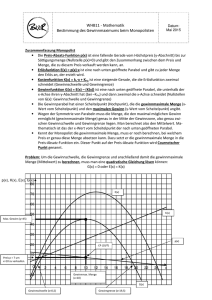
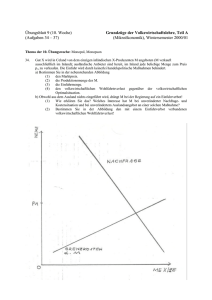
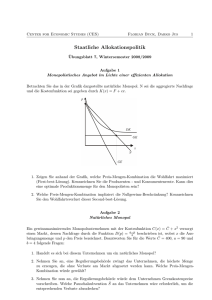
Wichtige Punkte und Zonen

Joel, Sebastian & Pete
Ökonomische Anwendung - Monopol
05.03.2008
Monopol
Ein Monopol nennt man eine Marktsituation (Marktform), in der für ein ökonomisches Gut nur ein
Anbieter existiert. Dadurch kann der Monopolist seinen Preis selbst wählen, muss aber auf die
Nachfrage achten. Ein höherer Preis hat immer einen geringeren Absatz zur Folge.
Daher versucht der Monopolist einen maximalen Gewinn zu erreichen indem er die gewinnmaximale
Ausbringungsmenge zum gewinnmaximalen Preis verkauft (Cournotscher Punkt).
In der Mathematik werden für diese wirtschaftliche Problematik folgende Polynomfunktionen
benutzt:
Die Kostenfunktion:
Wird durch eine kubische Polynomfunktion dargestellt. Diese Funktion ist monoton steigend, wobei
die Steigung der Funktion am Anfang und am Ende stärker ist. Dieses entspricht der Realität, da es
meistens mit hohen Kosten verbunden ist eine Produktion in Gang zu setzen und bei sehr hohen
Stückzahlen eine sehr hohe Belastung von Menschen und Maschinen zu hohen Ausfällen führt. Die
Kostenfunktion setzt sich aus den variablen Kosten(Kv) und den fixen Kosten(Kf) zusammen. Die
Stückkostenfunktion(k) ergibt sich indem man die Kostenfunktion(K) durch die Mengeneinheiten(ME)
teilt. Die variable Stückkostenfunktion(kv) ergibt sich indem man die variablen Kosten(Kv) durch die
ME teilt. Die Grenzkostenfunktion(K‘) ergibt sich durch ableiten der Kostenfunktion.
Bsp.:
Die Erlösfunktion:
Wird durch eine quadratische Polynomfunktion dargestellt. Diese Funktion ist eine nach unten
geöffnete Parabel. Sie ergibt sich wenn man die Preisabsatzfunktion(p) mit den ME multipliziert. Die
Grenzerlösfunktion(E‘) ergibt sich durch ableiten der Erlösfunktion(E).
Bsp.:
Die Gewinnfunktion:
Ist die Differenz von der Erlös- und Kostenfunktion. Die Schnittpunkte der Gewinnfunktion(G) sind die
Gewinnschwelle und Gewinngrenze. Die Gewinnschwelle ist ausschließlich die Produktionsmenge ab
dem das Unternehmen Gewinn macht. Die Gewinngrenze ist ausschließlich die Produktionsmenge ab
dem das Unternehmen kein Gewinn mehr macht.
Bsp.:
Joel, Sebastian & Pete
Ökonomische Anwendung - Monopol
05.03.2008
Wichtige Punkte und Zonen
Gewinnzone
G(x)
G‘(x)
G‘(x)
=
>
<
0
0
0
 Gewinnschwelle(Xs)
 Gewinngrenze(Xg)
oder
p(x) = k(x)
oder
K(x) = E(x)
IG= ]xs ,xg[
Gewinnmaximale Ausbringungsmenge
G‘(x) = 0
^
G‘‘(x)<0
oder
 Xmax( gewinnmaximale Ausbringungsmenge)
E‘(x)=K‘(x)
Maximaler Gewinn
G(Xmax)
Cournotscher Punkt
C(Xmax|p(Xmax))
Betriebsoptimum/-minimum
K‘(x) = k(x)
 Xbo
K‘(x) = kv(x)
 Xbm
Joel, Sebastian & Pete
Ökonomische Anwendung - Monopol
05.03.2008
Veranschaulichung wichtiger Veränderungen
Verhalten bei Änderung der Fixkosten
10
10
8
8
6
6
4
4
2
2
2
4
6
2
8
4
6
8
Verhalten bei Änderung der variablen Stückkosten um eine Konstante
10
10
8
8
6
6
4
4
2
2
2
4
6
8
2
4
6
8
Joel, Sebastian & Pete
Ökonomische Anwendung - Monopol
05.03.2008
Verhalten bei Änderung der Preisabsatzfunktion um eine Konstante
14
10
12
8
10
6
8
6
4
4
2
2
2
4
6
8
10
2
4
6
8
10