Übungen aus der Ökonomie 1) Gegeben sind die Kostenfunktion K

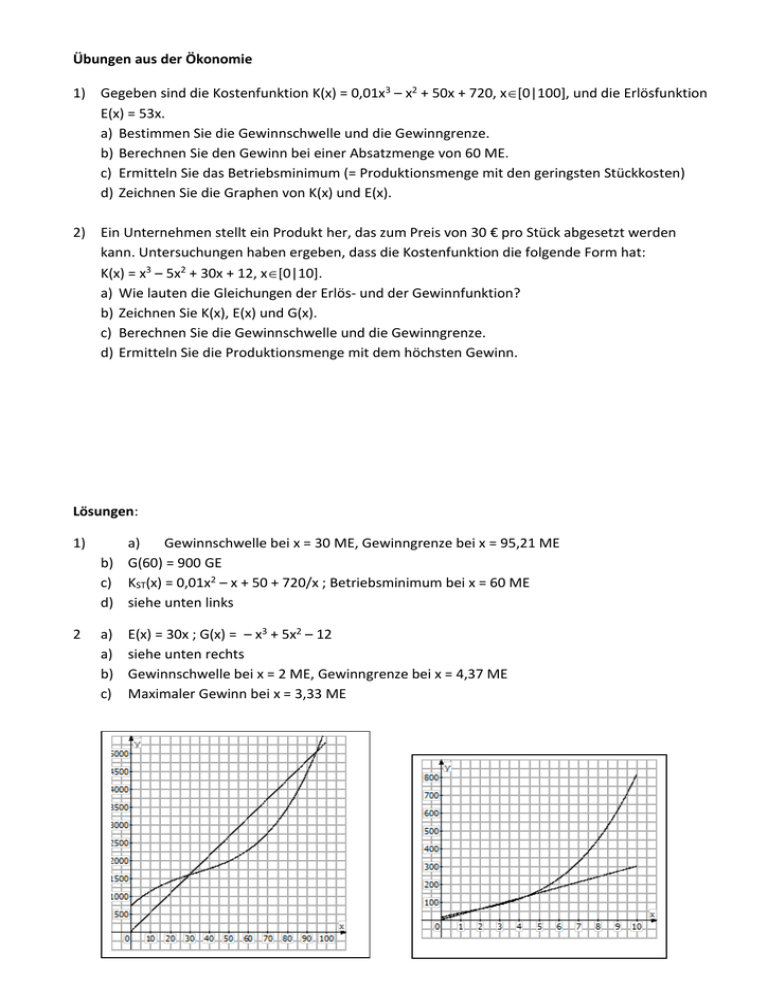
Übungen aus der Ökonomie
1) Gegeben sind die Kostenfunktion K(x) = 0,01x3 – x2 + 50x + 720, x[0|100], und die Erlösfunktion
E(x) = 53x.
a) Bestimmen Sie die Gewinnschwelle und die Gewinngrenze.
b) Berechnen Sie den Gewinn bei einer Absatzmenge von 60 ME.
c) Ermitteln Sie das Betriebsminimum (= Produktionsmenge mit den geringsten Stückkosten)
d) Zeichnen Sie die Graphen von K(x) und E(x).
2) Ein Unternehmen stellt ein Produkt her, das zum Preis von 30 € pro Stück abgesetzt werden
kann. Untersuchungen haben ergeben, dass die Kostenfunktion die folgende Form hat:
K(x) = x3 – 5x2 + 30x + 12, x[0|10].
a) Wie lauten die Gleichungen der Erlös- und der Gewinnfunktion?
b) Zeichnen Sie K(x), E(x) und G(x).
c) Berechnen Sie die Gewinnschwelle und die Gewinngrenze.
d) Ermitteln Sie die Produktionsmenge mit dem höchsten Gewinn.
Lösungen:
1)
a)
Gewinnschwelle bei x = 30 ME, Gewinngrenze bei x = 95,21 ME
b) G(60) = 900 GE
c) KST(x) = 0,01x2 – x + 50 + 720/x ; Betriebsminimum bei x = 60 ME
d) siehe unten links
2
a)
a)
b)
c)
E(x) = 30x ; G(x) = – x3 + 5x2 – 12
siehe unten rechts
Gewinnschwelle bei x = 2 ME, Gewinngrenze bei x = 4,37 ME
Maximaler Gewinn bei x = 3,33 ME