1 BERUFSKOLLEG DES MÄRKISCHEN KREISES IN ISERLOHN

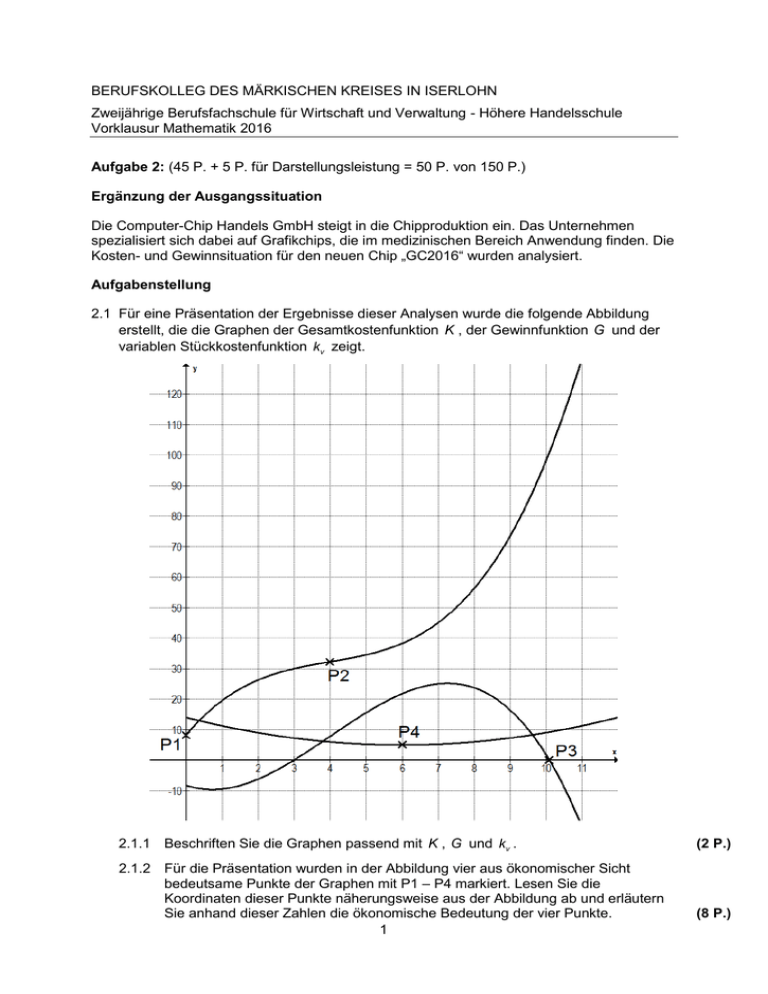
BERUFSKOLLEG DES MÄRKISCHEN KREISES IN ISERLOHN
Zweijährige Berufsfachschule für Wirtschaft und Verwaltung - Höhere Handelsschule
Vorklausur Mathematik 2016
Aufgabe 2: (45 P. + 5 P. für Darstellungsleistung = 50 P. von 150 P.)
Ergänzung der Ausgangssituation
Die Computer-Chip Handels GmbH steigt in die Chipproduktion ein. Das Unternehmen
spezialisiert sich dabei auf Grafikchips, die im medizinischen Bereich Anwendung finden. Die
Kosten- und Gewinnsituation für den neuen Chip „GC2016“ wurden analysiert.
Aufgabenstellung
2.1 Für eine Präsentation der Ergebnisse dieser Analysen wurde die folgende Abbildung
erstellt, die die Graphen der Gesamtkostenfunktion K , der Gewinnfunktion G und der
variablen Stückkostenfunktion kv zeigt.
2.1.1 Beschriften Sie die Graphen passend mit K , G und kv .
2.1.2 Für die Präsentation wurden in der Abbildung vier aus ökonomischer Sicht
bedeutsame Punkte der Graphen mit P1 – P4 markiert. Lesen Sie die
Koordinaten dieser Punkte näherungsweise aus der Abbildung ab und erläutern
Sie anhand dieser Zahlen die ökonomische Bedeutung der vier Punkte.
1
(2 P.)
(8 P.)
2.1.3 Bei der Erstellung der Abbildung wurde der Graph der linearen Erlösfunktion
nicht eingezeichnet. Ergänzen Sie in der Abbildung den fehlenden Graphen.
Geben Sie auch den zugehörigen Verkaufspreis pro ME des Chips an.
(4 P.)
2.2 Nach der Einführung eines neuen Produktionsverfahrens ist die neue
Gesamtkostenfunktion durch K ( x )  0,4x 3  3,2x 2  9,6x  22,2 gegeben.
Untersuchen Sie, bei welcher Produktionsmenge die Stückkosten minimal sind.
Geben Sie auch die minimalen Stückkosten an.
(9 P.)
2.3 Die Computer-Chip Handels GmbH hat einen neuen Spezialchip entwickelt und ist
Alleinanbieter dieses Produktes. Marktanalysen haben zu der Preis-Absatz-Funktion
p  x   3x  21 geführt. Als Gesamtkostenfunktion wurde
K ( x )  0,5x 3  4,5x 2  15x  5 ermittelt.
2.3.1 Geben Sie den Höchstpreis und die Sättigungsmenge an.
(2 P.)
2.3.2 Zeigen Sie, dass die Gewinnfunktion durch G  x   0,5x 3  1,5x 2  6x  5
gegeben ist.
(3 P.)
2.3.3 Bestimmen Sie Gewinnschwelle und –grenze und geben Sie an, in welchem
Preisbereich die Computer-Chip Handels GmbH sein neues Produkt anbieten
könnte, damit das Unternehmen Gewinn erzielt.
2.3.4. Ermitteln Sie auch den gewinnoptimalen Preis.
2
(8 P.)
(9 P.)
Lösungen:
2.1.1
2.1.2
2.1.3
2.2
Punkte
Beschriftung der Graphen s. rechts.
2
Ablesen / Erläutern der Punkte:
P1(0 | 8):
Die Fixkosten betragen 8 GE.
P2(4 | 32):
Bei einer Produktion von 4 ME
liegt der Übergang vom
degressiven zum progressiven
Kostenverlauf. Die
Gesamtkosten betragen dort ca.
32 GE.
P3(10,1 | 0):
Die Gewinngrenze liegt bei 10,1
ME.
P4(6 | 5):
Das Betriebsminimum beträgt 6
ME, die kurzfristige
Preisuntergrenze 5 GE/ME.
8
Graph der Erlösfunktion s. Abbildung oben
2
Verkaufspreis: 10 GE/ME.
2
Stückkosten: k ( x )  0,4 x  3,2x  9,6 
2
22,2
x
Gesucht ist der Tiefpunkt der Stückkostenfunktion:
k '  x   0,8 x  3,2 
22,2
44,4
und k ''  x   0,8 
2
x
x3
Notw. Bed.: k '  x   0  0,8 x  3,2 
22,2
 0  0,8 x 3  3,2x 2  22,2  0
x2
Mit Wertetabelle: Vorzeichenwechsel zwischen x=5 und x=6.
Verfeinerungen mithilfe der Wertetabellenfunktion des Taschenrechners ergeben:
x=5,0
x=5,1
x=5,07
x=5,08
-2,2
0,6888
-0,196
0,0967
Näherungslösung also x=5,08
Hinr. Bed.: k '( x )  0  k ''( x )  0
k ''  5,08   1,14  0  TP mit k  5,08   8,04 .
Bei einer Produktion von 5,08 ME sind die Stückkosten minimal und betragen dann 8,04
GE pro ME.
3
9
Lösungen:
2.3.1
Punkte
p  x   3x  21
Höchstpreis: p  0   21 GE/ME.
2.3.2
Sättigungsmenge: p  x   0  x  7 ME.
2
Gewinnfunktion bestimmen:
3
Gx  E x  K x

 3 x 2  21x  0,5 x 3  4,5 x 2  15 x  5

 0,5 x 3  1,5 x 2  6 x  5
2.3.3
Zunächst Gewinnschwelle und –grenze ermitteln:
9
Ansatz: G  x   0  0,5x  1,5x  6x  5  0
3
2
mit Wertetabelle: x1  5


Polynomdivision: 0,5 x 3  1,5 x 2  6 x  5 :  x  5   0,5 x 2  x  1
noch zu lösen: 0,5x 2  x  1  0
 x 2  2x  2  0  x2/3  1  3  x2  0,73,
x3  2,73  IDök
Gewinnschwelle bei 0,73 ME, Gewinngrenze bei 5 ME.
Zugehörige Preise bestimmen: p  0,73   18,81 und p  5   6 .
Der Chip kann zu Preisen zwischen 6 und 18,81 GE pro ME angeboten werden,
um Gewinn zu erzielen.
2.3.4
Zunächst Gewinnmaximum berechnen:
8
2
Ableitungen: G '  x   1,5x  3x  6 , G ''  x   3 x  3
Ansatz: G '  x   0
1,5x 2  3x  6  0  x 2  2x  4  0  x1/2  1  5  1  2,24
also x1  1,24  IDök , x2  3,24 .
Prüfen: G '  x   0  G ''  x   0
G ''  3,24   6,70  0  HP mit G  3,24   13,18 .
Gewinnoptimaler Preis: p  3,24   11,28 GE pro ME.
4