Monopolist - Mathe kann jeder

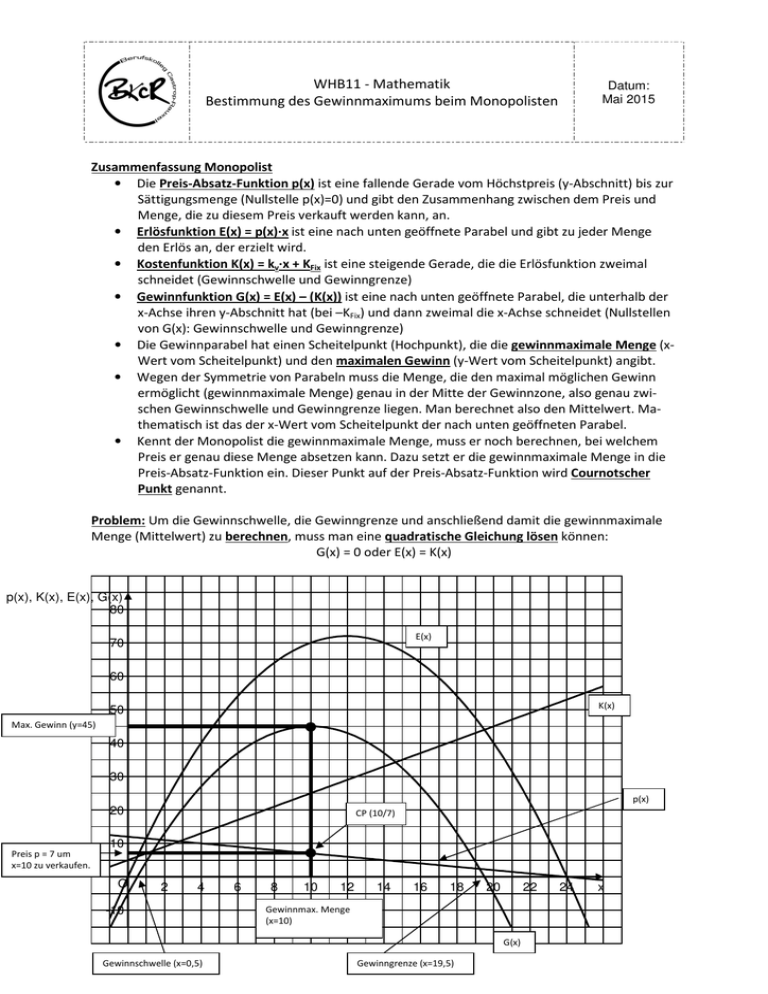
WHB11 - Mathematik
Bestimmung des Gewinnmaximums beim Monopolisten
Datum:
Mai 2015
Zusammenfassung Monopolist
• Die Preis-Absatz-Funktion p(x) ist eine fallende Gerade vom Höchstpreis (y-Abschnitt) bis zur
Sättigungsmenge (Nullstelle p(x)=0) und gibt den Zusammenhang zwischen dem Preis und
Menge, die zu diesem Preis verkauft werden kann, an.
• Erlösfunktion E(x) = p(x)∙x ist eine nach unten geöffnete Parabel und gibt zu jeder Menge
den Erlös an, der erzielt wird.
• Kostenfunktion K(x) = kv∙x + KFix ist eine steigende Gerade, die die Erlösfunktion zweimal
schneidet (Gewinnschwelle und Gewinngrenze)
• Gewinnfunktion G(x) = E(x) – (K(x)) ist eine nach unten geöffnete Parabel, die unterhalb der
x-Achse ihren y-Abschnitt hat (bei –KFix) und dann zweimal die x-Achse schneidet (Nullstellen
von G(x): Gewinnschwelle und Gewinngrenze)
• Die Gewinnparabel hat einen Scheitelpunkt (Hochpunkt), die die gewinnmaximale Menge (xWert vom Scheitelpunkt) und den maximalen Gewinn (y-Wert vom Scheitelpunkt) angibt.
• Wegen der Symmetrie von Parabeln muss die Menge, die den maximal möglichen Gewinn
ermöglicht (gewinnmaximale Menge) genau in der Mitte der Gewinnzone, also genau zwischen Gewinnschwelle und Gewinngrenze liegen. Man berechnet also den Mittelwert. Mathematisch ist das der x-Wert vom Scheitelpunkt der nach unten geöffneten Parabel.
• Kennt der Monopolist die gewinnmaximale Menge, muss er noch berechnen, bei welchem
Preis er genau diese Menge absetzen kann. Dazu setzt er die gewinnmaximale Menge in die
Preis-Absatz-Funktion ein. Dieser Punkt auf der Preis-Absatz-Funktion wird Cournotscher
Punkt genannt.
Problem: Um die Gewinnschwelle, die Gewinngrenze und anschließend damit die gewinnmaximale
Menge (Mittelwert) zu berechnen, muss man eine quadratische Gleichung lösen können:
G(x) = 0 oder E(x) = K(x)
p(x), K(x), E(x), G(x)
80
E(x)
70
60
K(x)
50
Max. Gewinn (y=45)
40
30
p(x)
20
Preis p = 7 um
x=10 zu verkaufen.
CP (10/7)
10
O
2
4
-10
6
8
10
12
14
16
18
20
22
Gewinnmax. Menge
(x=10)
G(x)
Gewinnschwelle (x=0,5)
Gewinngrenze (x=19,5)
24
x
WHB11 - Mathematik
Bestimmung des Gewinnmaximums beim Monopolisten
Datum:
Mai 2015
Weiteres Beispiel: Buch, Seite 167, Nr. 8
Preis-Absatz-Funktion p(x) = -0,5x + 3,5
Erlösfunktion E(x) = p(x)∙x = (-0,5x + 3,5)∙x = -0,5x² + 3,5x
Kostenfunktion K(x) = 0,5x + 2,5
Gewinnfunktion G(x) = E(x) – K(x) = -0,5x² + 3,5x – (0,5x + 2,5) = -0,5x² + 3x – 2,5
p(x), K(x), E(x), G(x)
8
7
6
5
4
3
2
1
O
1
2
3
4
5
6
7
8
9
10 x
-1
-2
-3
-4
Aufgaben:
Beschriften bzw. markieren Sie im Diagramm die
• Preis-Absatz-Funktion p(x), die Kostenfunktion K(x), die Erlösfunktion E(x) und die
Gewinnfunktion G(x)
• den Höchstpreis und die Sättigungsmenge
• die Gewinnschwelle und die Gewinngrenze
• die gewinnmaximale Menge und den maximalen Gewinn
• den Preis, den der Monopolist festsetzen muss, um maximalen Gewinn zu erzielen
• den Cournotschen Punkt
Problem: Und wie geht das Ganze rechnerisch????????