4. WH
Werbung

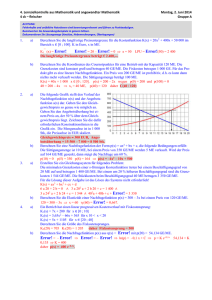
4. Lernzielkontrolle aus Mathematik und angewandter Mathematik 4 ak – löffler Montag, 2. Juni 2014 Gruppe A ACHTUNG: Fehlerhafte und unübliche Notationen sind bewertungsrelevant und führen zu Punkteabzügen. Beantworten Sie Anwendungsbeispiele in ganzen Sätzen. Dokumentieren Sie Lösungswege (Ansätze, Nebenrechnungen, Überlegungen) 1. 2. 3. 4. a) Berechnen Sie die Gewinngrenzen für die Kostenfunktion K(x) = 10x2 + 300x + 160 und den Preis 500 GE/ME im Bereich x ∈ [0 ; 50]. K in Euro, x in ME. K(x) = 500 x x1 = 0,83 ME und x2 = 19,17 ME b) Berechnen Sie die langfristige Preisuntergrenze für einen Betrieb mit der Kapazität 50 ME. Die Grenzkosten sind konstant groß und betragen 40 GE/ME. Die Fixkosten betragen 1 000 GE. – K; (50) = 40 + Error! = 60 GE/ME a) Die folgende Grafik stellt den Verlauf der Durchschnittskosten dar. Lesen Sie aus der Grafik so genau wie möglich die langfristige Preisuntergrenze ab. Geben Sie die Gewinngrenzen für einen Preis an, der um 50 % über der langfristigen Preisuntergrenze liegt. Zeichnen Sie die dazu nötigen Konstruktionslinien in die Grafik ein. LPU 6 000 Gewinngrenzen bei p = 9 000 sind ca. 6 und 37 b) Berechnen Sie die Gleichung einer progressiven Kostenfunktion mit: Die Grenzkosten beim Beschäftigungsgrad 8 ME sind 37 GE/ME, die Kosten beim gleichen Beschäftigungsgrad sind 501 GE und die Fixkosten betragen 333 GE. 2a8 + b = 37 a 82 + 8b + 333 = 501 K(x) = 2x2 + 5x + 333 a) Ermitteln Sie den Gleichgewichtspreis für eine Produkt mit einer Sättigungsmenge von 50 ME und dem Prohibitivpreis von 500 EUR/ME. Das Angebot verhält sich wie a(x) = 5x + 50. Berechnen Sie den Nachfrageüberhang bei einem Preis, der 20 % unter dem Gleichgewichtspreis liegt. n(x) = 500 – 10x Gleichgewicht 500 – 10x = 5x + 50 x = 30 mit p(30) = 200 a(22) = 160 und n(34) = 160 daher Nachfrageüberhang von 12 ME b) Berechnen Sie die Gleichung einer linearen Nachfragefunktion aus: Bei einem Preis von 200 GE/ME können 50 ME abgesetzt werden. Die Elastizität bei einer Menge von 40 ME beträgt 2,75. 200 = 50a + b und 2,75 = Error! a = –2 und b = 300 daher p(x) = 300 – 2x a) Ein Betrieb hat einen linear progressiven Kostenverlauf mit Fixkostensprung: K1(x) = 7x + 200 für x ∈ [0 ; 10] K2(x) = 3,65x2 – 66x + 565 für x 10 < x < 20 K3(x) = 5x + 705 für x ∈ [20 ; 40] Berechnen Sie die langfristige Preisuntergrenze. – – – K; 1(10) = 27 K; 2(12,442) = 24,824 K; 3(40) = 22,63 also LPU = 22,63 GE/ME Berechnen Sie die Nachfragefunktion p(x) aus η(x) = Error! mit p(20) = 360 GE/ME. Error! = – Error! Error! = – Error! ln(p) = ln(200 – x) + C p = K (200 – x) 360 = K 180 K = 2 daher p(x) = 400 – 2x. b) 4. Lernzielkontrolle aus Mathematik und angewandter Mathematik 4 ak – löffler ACHTUNG: Fehlerhafte und unübliche Notationen sind bewertungsrelevant und führen zu Punkteabzügen. Beantworten Sie Anwendungsbeispiele in ganzen Sätzen. Dokumentieren Sie Lösungswege (Ansätze, Nebenrechnungen, Überlegungen) Montag, 2. Juni 2014 Gruppe B 1. 2. 3. 4. a) Berechnen Sie die Gewinngrenzen für die Kostenfunktion K(x) = 8x 2 + 200x + 160 und den Preis 300 GE/ME im Bereich x ∈ [0 ; 50]. K in Euro, x in ME. K(x) = 300 x x1 = 1,88 ME und x2 = 10,62 ME b) Berechnen Sie die langfristige Preisuntergrenze für einen Betrieb mit der Kapazität 50 ME. Die Grenzkosten sind konstant groß und betragen 40 GE/ME. Die Fixkosten betragen 600 GE. – K; (50) = 40 + Error! = 52 GE/ME a) Die folgende Grafik stellt den Verlauf der Durchschnittskosten dar. Lesen Sie aus der Grafik so genau wie möglich die langfristige Preisuntergrenze ab. Geben Sie die Gewinngrenzen für einen Preis an, der um 50 % über der langfristigen Preisuntergrenze liegt. Zeichnen Sie die dazu nötigen Konstruktionslinien in die Grafik ein. LPU 6 000 Gewinngrenzen bei p = 9 000 sind ca. 6 und 37 b) Berechnen Sie die Gleichung einer progressiven Kostenfunktion mit: Die Grenzkosten beim Beschäftigungsgrad 8 ME sind 74 GE/ME, die Kosten beim gleichen Beschäftigungsgrad sind 1 002 GE und die Fixkosten betragen 666 GE. 2a8 + b = 74 a 82 + 8b + 333 = 1 002 K(x) = 4x2 + 10x + 666 a) Ermitteln Sie den Gleichgewichtspreis für eine Produkt mit einer Sättigungsmenge von 50 ME und dem Prohibitivpreis von 500 EUR/ME. Das Angebot verhält sich wie a(x) = 5x + 200. Berechnen Sie den Nachfrageüberhang bei einem Preis, der 20 % unter dem Gleichgewichtspreis liegt. n(x) = 500 – 10x Gleichgewicht 500 – 10x = 5x + 200 x = 20 mit p(20) = 300 a(8) = 240 und n(26) = 240 daher Nachfrageüberhang von 18 ME b) Berechnen Sie die Gleichung einer linearen Nachfragefunktion aus: Bei einem Preis von 400 GE/ME können 50 ME abgesetzt werden. Die Elastizität bei einer Menge von 40 ME beträgt 5,25. 400 = 50a + b und 5,25 = Error! a = –2 und b = 500 daher p(x) = 500 – 2x a) Ein Betrieb hat einen linear progressiven Kostenverlauf mit Fixkostensprung: K1(x) = 7x + 200 für x ∈ [0 ; 10] K2(x) = 3,65x2 – 66x + 565 für x 10 < x < 20 K3(x) = 5x + 705 für x ∈ [20 ; 50] Berechnen Sie die langfristige Preisuntergrenze. – – – K; 1(10) = 27 K; 2(12,442) = 24,824 K; 3(50) = 19,1 also LPU = 19,1 GE/ME Berechnen Sie die Nachfragefunktion p(x) aus η(x) = Error! mit p(20) = 720 GE/ME. Error! = – Error! Error! = – Error! ln(p) = ln(200 – x) + C p = K (200 – x) 720 = K 180 K = 4 daher p(x) = 800 – 4x. b) 4. Lernzielkontrolle aus Mathematik und angewandter Mathematik 4 ak – löffler ACHTUNG: Fehlerhafte und unübliche Notationen sind bewertungsrelevant und führen zu Punkteabzügen. Beantworten Sie Anwendungsbeispiele in ganzen Sätzen. Dokumentieren Sie Lösungswege (Ansätze, Nebenrechnungen, Überlegungen) Montag, 2. Juni 2014 Gruppe A 1. 2. 3. 4. a) Berechnen Sie die Gewinngrenzen für die Kostenfunktion K(x) = 10x 2 + 300x + 160 und den Preis 500 GE/ME im Bereich x ∈ [0 ; 50]. K in Euro, x in ME. b) Berechnen Sie die langfristige Preisuntergrenze für einen Betrieb mit der Kapazität 50 ME. Die Grenzkosten sind konstant groß und betragen 40 GE/ME. Die Fixkosten betragen 1 000 GE. a) Die folgende Grafik stellt den Verlauf der Durchschnittskosten dar. Lesen Sie aus der Grafik so genau wie möglich die langfristige Preisuntergrenze ab. Geben Sie die Gewinngrenzen für einen Preis an, der um 50 % über der langfristigen Preisuntergrenze liegt. Zeichnen Sie die dazu nötigen Konstruktionslinien in die Grafik ein. b) Berechnen Sie die Gleichung einer progressiven Kostenfunktion mit: Die Grenzkosten beim Beschäftigungsgrad 8 ME sind 37 GE/ME, die Kosten beim gleichen Beschäftigungsgrad sind 501 GE und die Fixkosten betragen 333 GE. a) Ermitteln Sie den Gleichgewichtspreis für eine Produkt mit einer Sättigungsmenge von 50 ME und dem Prohibitivpreis von 500 EUR/ME. Das Angebot verhält sich wie a(x) = 5x + 50. Berechnen Sie den Nachfrageüberhang bei einem Preis, der 20 % unter dem Gleichgewichtspreis liegt. b) Berechnen Sie die Gleichung einer linearen Nachfragefunktion aus: Bei einem Preis von 200 GE/ME können 50 ME abgesetzt werden. Die Elastizität bei einer Menge von 40 ME beträgt 2,75. a) Ein Betrieb hat einen linear progressiven Kostenverlauf mit Fixkostensprung: K1(x) = 7x + 200 für x ∈ [0 ; 10] K2(x) = 3,65x2 – 66x + 565 für x 10 < x < 20 K3(x) = 5x + 705 für x ∈ [20 ; 40] Berechnen Sie die langfristige Preisuntergrenze. b) Berechnen Sie die Nachfragefunktion p(x) aus η(x) = Error! mit p(20) = 360 GE/ME. 4. Lernzielkontrolle aus Mathematik und angewandter Mathematik 4 ak – löffler Montag, 2. Juni 2014 Gruppe B ACHTUNG: Fehlerhafte und unübliche Notationen sind bewertungsrelevant und führen zu Punkteabzügen. Beantworten Sie Anwendungsbeispiele in ganzen Sätzen. Dokumentieren Sie Lösungswege (Ansätze, Nebenrechnungen, Überlegungen) 1. 2. 3. 4. a) Berechnen Sie die Gewinngrenzen für die Kostenfunktion K(x) = 8x 2 + 200x + 160 und den Preis 300 GE/ME im Bereich x ∈ [0 ; 50]. K in Euro, x in ME. b) Berechnen Sie die langfristige Preisuntergrenze für einen Betrieb mit der Kapazität 50 ME. Die Grenzkosten sind konstant groß und betragen 40 GE/ME. Die Fixkosten betragen 600 GE. a) Die folgende Grafik stellt den Verlauf der Durchschnittskosten dar. Lesen Sie aus der Grafik so genau wie möglich die langfristige Preisuntergrenze ab. Geben Sie die Gewinngrenzen für einen Preis an, der um 50 % über der langfristigen Preisuntergrenze liegt. Zeichnen Sie die dazu nötigen Konstruktionslinien in die Grafik ein. b) Berechnen Sie die Gleichung einer progressiven Kostenfunktion mit: Die Grenzkosten beim Beschäftigungsgrad 8 ME sind 74 GE/ME, die Kosten beim gleichen Beschäftigungsgrad sind 1 002 GE und die Fixkosten betragen 666 GE. a) Ermitteln Sie den Gleichgewichtspreis für eine Produkt mit einer Sättigungsmenge von 50 ME und dem Prohibitivpreis von 500 EUR/ME. Das Angebot verhält sich wie a(x) = 5x + 200. Berechnen Sie den Nachfrageüberhang bei einem Preis, der 20 % unter dem Gleichgewichtspreis liegt. b) Berechnen Sie die Gleichung einer linearen Nachfragefunktion aus: Bei einem Preis von 400 GE/ME können 50 ME abgesetzt werden. Die Elastizität bei einer Menge von 40 ME beträgt 5,25. a) Ein Betrieb hat einen linear progressiven Kostenverlauf mit Fixkostensprung: K1(x) = 7x + 200 für x ∈ [0 ; 10] K2(x) = 3,65x2 – 66x + 565 für x 10 < x < 20 K3(x) = 5x + 705 für x ∈ [20 ; 50] Berechnen Sie die langfristige Preisuntergrenze. b) Berechnen Sie die Nachfragefunktion p(x) aus η(x) = Error! mit p(20) = 720 GE/ME.