3. Schriftliche Wiederholung aus Physik Donnerstag, 27. Februar 1997

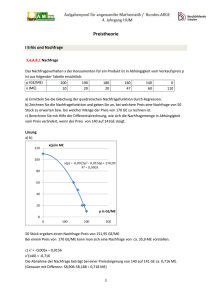
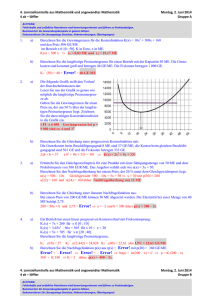
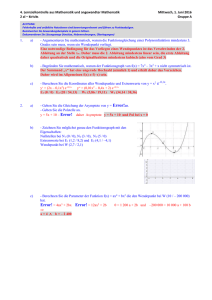
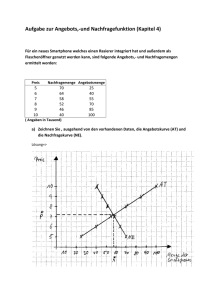
4. Lernzielkontrolle aus Mathematik und angewandter Mathematik
4 ck – fleischer
Montag, 2. Juni 2014
Gruppe A
ACHTUNG:
Fehlerhafte und unübliche Notationen sind bewertungsrelevant und führen zu Punkteabzügen.
Beantworten Sie Anwendungsbeispiele in ganzen Sätzen.
Dokumentieren Sie Lösungswege (Ansätze, Nebenrechnungen, Überlegungen)
1.
2.
a)
Berechnen Sie die langfristige Preisuntergrenze für die Kostenfunktion K(x) = 20x 2 + 400x + 50 000 im
Bereich x ∈ [0 ; 100]. K in Euro, x in ME.
–
K; (x) = Error!
Error! = 20 – Error! = 0  x = 50 LPU = Error!(50) = 2 400
Die langfristige Preisuntergrenze beträgt € 2.400,--.
b)
Berechnen Sie die Koordinaten des Cournotpunktes für eine Betrieb mit der Kapazität 120 ME. Die
Grenzkosten sind konstant groß und betragen 40 GE/ME. Die Fixkosten betragen 1 000 GE. Für das Produkt gibt es eine lineare Nachfragefunktion. Ein Preis von 200 GE/ME ist prohibitiv, d.h. es kann dann
nichts mehr verkauft werden. Die Sättigungsmenge beträgt 100 ME.
K(x) = 40x + 1 000 x ∈ [0 ; 120]. p(x) = 200 – 2x wegen p(0) = 200 und p(100) = 0
40 = 200 – 4x  xc = 40 ME, p(40) = 120 daher C(40 / 120)
a)
Die folgende Grafik stellt den Verlauf der
Nachfragefunktion n(x) und der Angebotsfunktion a(x) dar. Geben Sie den Gleichgewichtspreis so genau wie möglich an.
Geben Sie den Angebotsüberhang bei einem Preis an, der 50 % über dem Gleichgewichtspreis liegt. Zeichnen Sie die dafür
erforderlichen Konstruktionslinien in die
Grafik ein. Die Mengenachse ist in 1 000
Stk, die Preisachse in EUR skaliert.
Gleichgewichtspreis  300 EUR, Angebotsüberhang = 15 500 – 7 000 = 8 500 Stk.
Berechnen Sie eine Nachfragefunktion der Form p(x) = ax2 + bx + c, die folgende Bedingungen erfüllt:
Die Sättigungsmenge ist 10 ME, bei einem Preis von 350 GE/ME werden 5 ME verkauft. Wird der Preis
auf 164 GE/ME gesenkt, dann steigt die Nachfrage um 60 %.
p(10) = 0 p(5) = 350 p(8) = 164  p(x) = –4x2 – 10x + 500
Erstellen Sie ein Gleichungssystem für folgendes Problem:
Die minimalen Grenzkosten einer s-förmigen Kostenfunktion treten bei einem Beschäftigungsgrad von
20 ME auf und betragen 1 400 GE/ME. Bei einem um 20 % höheren Beschäftigungsgrad sind die Grenzkosten 1 544 GE/ME. Die Stückkosten beim Beschäftigungsgrad 40 ME betragen 3 350 GE/ME.
Für die Lösung dieser Aufgabe ist das Lösen des Systems nicht erforderlich!
K(x) = ax3 + bx2 + cx + d
6 a 20 + 2 b = 0 ∧ 3 a 202 a + 2 b 20 + c = 1 400 ∧
3 a 242 a + 2 b 24 + c = 1 544 ∧ 402a + 40b + c + Error! = 3 350
Berechnen Sie die Elastizität einer Nachfragefunktion p(x) = 300 – 3x bei einem Preis von 120 GE/ME.
120 = 300 – 3x  x = 60 η (60) = Error! = 0,667.
Ein Betrieb hat einen linear progressiven Kostenverlauf mit Fixkostensprung:
K1(x) = 7x + 200 für x ∈ [0 ; 10]
K2(x) = 3,65x2 – 66x + 565 für x 10 < x < 20
K3(x) = 5x + 1105 für x ∈ [20 ; 40]
Berechnen Sie die Größe des Fixkostensprunges.
K2(20) = 705 K3(20) = 1 205
daher Fixkostensprung = 500
Berechnen Sie die Nachfragefunktion p(x) aus η(x) = Error! mit p(20) = 54,134 GE/ME.
Error! = – Error!  Error! = – Error!  ln(p) = –0,1 x + C  p = K e–0,1x 54,134 = K
0,135  K = 400
daher p(x) = 400 e–0,1x.
b)
3.
a)
b)
4.
a)
b)
4. Lernzielkontrolle aus Mathematik und angewandter Mathematik
4 ck – fleischer
Montag, 2. Juni 2014
Gruppe B
ACHTUNG:
Fehlerhafte und unübliche Notationen sind bewertungsrelevant und führen zu Punkteabzügen.
Beantworten Sie Anwendungsbeispiele in ganzen Sätzen.
Dokumentieren Sie Lösungswege (Ansätze, Nebenrechnungen, Überlegungen)
1.
2.
a)
Berechnen Sie die langfristige Preisuntergrenze für die Kostenfunktion K(x) = 2x2 + 40x + 5 000 im Bereich x ∈ [0 ; 100]. K in Euro, x in ME.
–
K; (x) = Error!
Error! = 2 – Error! = 0  x = 50 LPU = Error!(50) = 240
Die langfristige Preisuntergrenze beträgt € 240,--.
b)
Berechnen Sie die Koordinaten des Cournotpunktes für eine Betrieb mit der Kapazität 120 ME. Die
Grenzkosten sind konstant groß und betragen 4 GE/ME. Die Fixkosten betragen 100 GE. Für das Produkt
gibt es eine lineare Nachfragefunktion. Ein Preis von 20 GE/ME ist prohibitiv, d.h. es kann dann nichts
mehr verkauft werden. Die Sättigungsmenge beträgt 100 ME.
K(x) = 4x + 100 x ∈ [0 ; 120]. p(x) = 20 – 0,2 x wegen p(0) = 20 und p(100) = 0
4 = 20 – 0,4x  xc = 40 ME, p(40) = 12 daher C(40 / 12)
a)
Die folgende Grafik stellt den Verlauf der
Nachfragefunktion n(x) und der Angebotsfunktion a(x) dar. Geben Sie den Gleichgewichtspreis so genau wie möglich an.
Geben Sie den Angebotsüberhang bei einem Preis an, der 50 % über dem Gleichgewichtspreis liegt. Zeichnen Sie die dafür
erforderlichen Konstruktionslinien in die
Grafik ein. Die Mengenachse ist in 1 000
Stk, die Preisachse in EUR skaliert.
Gleichgewichtspreis  300 EUR, Angebotsüberhang = 15 500 – 7 000 = 8 500 Stk.
Berechnen Sie eine Nachfragefunktion der Form p(x) = ax2 + bx + c, die folgende Bedingungen erfüllt:
Die Sättigungsmenge ist 10 ME, bei einem Preis von 700 GE/ME werden 5 ME verkauft. Wird der Preis
auf 328 GE/ME gesenkt, dann steigt die Nachfrage um 60 %.
p(10) = 0 p(5) = 700 p(8) = 328  p(x) = –8x2 – 20x + 1 000
Erstellen Sie ein Gleichungssystem für folgendes Problem:
Die minimalen Grenzkosten einer s-förmigen Kostenfunktion treten bei einem Beschäftigungsgrad von
20 ME auf und betragen 700 GE/ME. Bei einem um 20 % höheren Beschäftigungsgrad sind die Grenzkosten 772 GE/ME. Die Stückkosten beim Beschäftigungsgrad 40 ME betragen 1 675 GE/ME.
Für die Lösung dieser Aufgabe ist das Lösen des Systems nicht erforderlich!
K(x) = ax3 + bx2 + cx + d
6 a 20 + 2 b = 0 ∧ 3 a 202 a + 2 b 20 + c = 700 ∧
3 a 242 a + 2 b 24 + c = 772 ∧ 402a + 40b + c + Error! = 1 675
Berechnen Sie die Elastizität einer Nachfragefunktion p(x) = 300 – 3x bei einem Preis von 180 GE/ME.
180 = 300 – 3x  x = 40 η (40) = Error! = 1,5.
Ein Betrieb hat einen linear progressiven Kostenverlauf mit Fixkostensprung:
K1(x) = 7x + 200 für x ∈ [0 ; 10]
K2(x) = 3,65x2 – 66x + 565 für x 10 < x < 20
K3(x) = 5x + 905 für x ∈ [20 ; 40]
Berechnen Sie die Größe des Fixkostensprunges.
K2(20) = 705 K3(20) = 1 005
daher Fixkostensprung = 300
Berechnen Sie die Nachfragefunktion p(x) aus η(x) = Error! mit p(20) = 27,067 GE/ME.
Error! = – Error!  Error! = – Error!  ln(p) = –0,1 x + C  p = K e–0,1x 27,067 = K
0,135  K = 200
daher p(x) = 200 e–0,1x.
b)
3.
a)
b)
4.
a)
b)
4. Lernzielkontrolle aus Mathematik und angewandter Mathematik
4 ck – fleischer
ACHTUNG:
Fehlerhafte und unübliche Notationen sind bewertungsrelevant und führen zu Punkteabzügen.
Beantworten Sie Anwendungsbeispiele in ganzen Sätzen.
Dokumentieren Sie Lösungswege (Ansätze, Nebenrechnungen, Überlegungen)
Montag, 2. Juni 2014
Gruppe A
1.
2.
3.
4.
a)
Berechnen Sie die langfristige Preisuntergrenze für die Kostenfunktion
K(x) = 20x2 + 400x + 50 000 im Bereich x ∈ [0 ; 100]. K in Euro, x in ME.
b)
Berechnen Sie die Koordinaten des Cournotpunktes für eine Betrieb mit der Kapazität 120 ME. Die
Grenzkosten sind konstant groß und betragen 40 GE/ME. Die Fixkosten betragen 1 000 GE. Für das Produkt gibt es eine lineare Nachfragefunktion. Ein Preis von 200 GE/ME ist prohibitiv, d.h. es kann dann
nichts mehr verkauft werden. Die Sättigungsmenge beträgt 100 ME.
a)
Die folgende Grafik stellt den Verlauf der Nachfragefunktion n(x) und der Angebotsfunktion a(x) dar.
Geben Sie den Gleichgewichtspreis so genau wie möglich an. Geben Sie den Angebotsüberhang bei einem Preis an, der 50 % über dem Gleichgewichtspreis liegt. Zeichnen Sie die dafür erforderlichen Konstruktionslinien in die Grafik ein. Die Mengenachse ist in 1 000 Stk, die Preisachse in EUR skaliert.
b)
Berechnen Sie eine Nachfragefunktion der Form p(x) = ax2 + bx + c, die folgende Bedingungen erfüllt:
Die Sättigungsmenge ist 10 ME, bei einem Preis von 350 GE/ME werden 5 ME verkauft.
Wird der Preis auf 164 GE/ME gesenkt, dann steigt die Nachfrage um 60 %.
a)
Erstellen Sie ein Gleichungssystem für folgendes Problem:
Die minimalen Grenzkosten einer s-förmigen Kostenfunktion treten bei einem Beschäftigungsgrad von
20 ME auf und betragen 1 400 GE/ME. Bei einem um 20 % höheren Beschäftigungsgrad sind die Grenzkosten 1 544 GE/ME. Die Stückkosten beim Beschäftigungsgrad 40 ME betragen 3 350 GE/ME.
Für die Lösung dieser Aufgabe ist das Lösen des Systems nicht erforderlich!
b)
Berechnen Sie die Elastizität einer Nachfragefunktion p(x) = 300 – 3x bei einem Preis von 120 GE/ME.
a)
Ein Betrieb hat einen linear progressiven Kostenverlauf mit Fixkostensprung:
K1(x) = 7x + 200 für x ∈ [0 ; 10]
K2(x) = 3,65x2 – 66x + 565 für x 10 < x < 20
K3(x) = 5x + 1105 für x ∈ [20 ; 40]
Berechnen Sie die Größe des Fixkostensprunges.
b)
Berechnen Sie die Nachfragefunktion p(x) aus η(x) =
Error! mit p(20) = 54,134 GE/ME.
4. Lernzielkontrolle aus Mathematik und angewandter Mathematik
4 ck – fleischer
ACHTUNG:
Fehlerhafte und unübliche Notationen sind bewertungsrelevant und führen zu Punkteabzügen.
Beantworten Sie Anwendungsbeispiele in ganzen Sätzen.
Dokumentieren Sie Lösungswege (Ansätze, Nebenrechnungen, Überlegungen)
Montag, 2. Juni 2014
Gruppe B
1.
2.
3.
4.
a)
Berechnen Sie die langfristige Preisuntergrenze für die Kostenfunktion K(x) = 2x 2 + 40x + 5 000 im Bereich x ∈ [0 ; 100]. K in Euro, x in ME.
b)
Berechnen Sie die Koordinaten des Cournotpunktes für eine Betrieb mit der Kapazität 120 ME. Die
Grenzkosten sind konstant groß und betragen 4 GE/ME. Die Fixkosten betragen 100 GE. Für das Produkt
gibt es eine lineare Nachfragefunktion. Ein Preis von 20 GE/ME ist prohibitiv, d.h. es kann dann nichts
mehr verkauft werden. Die Sättigungsmenge beträgt 100 ME.
a)
Die folgende Grafik stellt den Verlauf der Nachfragefunktion n(x) und der Angebotsfunktion a(x) dar.
Geben Sie den Gleichgewichtspreis so genau wie möglich an. Geben Sie den Angebotsüberhang bei einem Preis an, der 50 % über dem Gleichgewichtspreis liegt. Zeichnen Sie die dafür erforderlichen Konstruktionslinien in die Grafik ein. Die Mengenachse ist in 1 000 Stk, die Preisachse in EUR skaliert.
b)
Berechnen Sie eine Nachfragefunktion der Form p(x) = ax2 + bx + c, die folgende Bedingungen erfüllt:
Die Sättigungsmenge ist 10 ME, bei einem Preis von 700 GE/ME werden 5 ME verkauft. Wird der Preis
auf 328 GE/ME gesenkt, dann steigt die Nachfrage um 60 %.
a)
Erstellen Sie ein Gleichungssystem für folgendes Problem:
Die minimalen Grenzkosten einer s-förmigen Kostenfunktion treten bei einem Beschäftigungsgrad von
20 ME auf und betragen 700 GE/ME. Bei einem um 20 % höheren Beschäftigungsgrad sind die Grenzkosten 772 GE/ME. Die Stückkosten beim Beschäftigungsgrad 40 ME betragen 1 675 GE/ME.
Für die Lösung dieser Aufgabe ist das Lösen des Systems nicht erforderlich!
b)
Berechnen Sie die Elastizität einer Nachfragefunktion p(x) = 300 – 3x bei einem Preis von 180 GE/ME.
a)
Ein Betrieb hat einen linear progressiven Kostenverlauf mit Fixkostensprung:
K1(x) = 7x + 200 für x ∈ [0 ; 10]
K2(x) = 3,65x2 – 66x + 565 für x 10 < x < 20
K3(x) = 5x + 905 für x ∈ [20 ; 40]
Berechnen Sie die Größe des Fixkostensprunges.
b)
Berechnen Sie die Nachfragefunktion p(x) aus η(x) =
Error! mit p(20) = 27,067 GE/ME.