4. LZK
Werbung

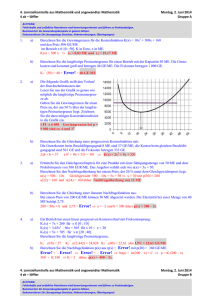
4. Lernzielkontrolle aus Mathematik und angewandter Mathematik 2 al – kirisits Mittwoch, 1. Juni 2016 Gruppe A ACHTUNG: Fehlerhafte und unübliche Notationen sind bewertungsrelevant und führen zu Punkteabzügen. Beantworten Sie Anwendungsbeispiele in ganzen Sätzen. Dokumentieren Sie Lösungswege (Ansätze, Nebenrechnungen, Überlegungen) 1. 2. a) - Argumentieren Sie mathematisch, warum die Funktionsgleichung einer Polynomfunktion mindestens 3. Grades sein muss, wenn ein Wendepunkt vorliegt. Eine notwendige Bedingung für das Vorliegen eines Wendepunktes ist das Verschwinden der 2. Ableitung an der Stelle xw. Daher muss die 2. Ableitung mindestens linear sein, die erste Ableitung daher quadratisch und die Originalfunktion mindestens kubisch (also vom Grad 3) b) - Begründen Sie mathematisch, warum der Funktionsgraph von f(x) = 7x 4 – 3x2 + x nicht symmetrisch ist. Der Summand „x“ hat eine ungerade Hochzahl (nämlich 1) und erhält daher das Vorzeichen. Daher wird im Allgemeinen f(x) f(–x) sein. c) - Berechnen Sie die Koordinaten aller Wendepunkte und Extremwerte von y = x 2 e–0,1x. y‘ = (2x – 0,1x2) e–0,1x y“ = (0,01x2 – 0,4x + 2) e–0,1x E1 (0 / 0) E2 (20 / 54,13) W1 (5,86 / 19,11) W2 (34,14 / 38,36) a) - Geben Sie die Gleichung der Asymptote von y = Error!an. - Geben Sie die Polstelle an. y = 5x + 10 – Error! daher Asymptote: y = 5x + 10 und Pol bei x = 0 b) - Zeichnen Sie möglichst genau den Funktionsgraph mit den Eigenschaften: Nullstellen bei N1 (0 / 0), N2 (3 / 0), N3 (5 / 0) Extremwerte bei E1 (1,2 / 8,2) und E2 (4,1 / –4,1) Wendepunkt bei W (2,7 / 2,1) c) - Berechnen Sie die Parameter der Funktion f(x) = ax4 + bx2 die den Wendepunkt bei W (10 / – 200 000) hat. Error! = 4ax3 + 2bx Error! = 12ax2 + 2b 0 = 1 200 a + 2b und –200 000 = 10 000 a + 100 b a = 4 ∧ b = – 2 400 A 3. a) Ein Swimmingpool hat die Form eines Rechtecks mit zwei angesetzten Halbkreisen (siehe Skizze). Die Fläche soll 70 m2 betragen. - Berechnen Sie die Abmessungen x und r so, dass die Kosten für die Umrahmung möglichst klein werden, wenn die Rundungen doppelt so teuer wie die geraden Randstücke sind Z(x,r) = 2 · 2 r + 2x → Minimum mit 70 = r2 + 2rx x = Error! Z(r) = 4 r + 2 · Error! Error! = 4 – Error! – = 0 r = Error! = 2,73 m und r = 2,73 m und x = 8,56 m b) Zwei Punkte A und B sind mit einer Rohrleitung zu verbinden. Die Strecke AX kostet um 80 % mehr als die Strecke BX. - Berechnen Sie die Länge der Strecken AX und BX, damit die Verbindung kostenoptimal wird. a = 40 m, b = 80 m Z(x) = x + 1,8 53,27 4. a) (80 – x)2 + 402 Error! = 0 x = 26,73 m und AX = 48,11 m und BX = Die nebenstehende Grafik stellt die Angebots- und Nachfragefunktion eines Produktes dar. - Bestimmen Sie aus der Grafik den Gleichgewichtspreis. - Bestimmen Sie den Nachfrageüberhang für einen Preis, der um 25 % geringer als der Gleichgewichtspreis ist. - Interpretieren Sie die Nullstelle der Nachfragefunktion und die Achsenschnittpunkte mit der Preisachse. Zeichnen Sie die Hilfslinien in die Grafik ein. Gleichgewichtspreis = 2 154 EUR/ME Nachfrageüberhang bei p = 1 616 = 16,9 – 10,1 = 6,8 ME 25 ME ist die Sättigungsmenge, mehr wird nicht nachgefragt 5 000 EUR/ME ist prohibitiv, d.h. bei diesem Preis wird nichts nachgefragt 1 000 EUR/ME ist der Preis, bei dem nichts mehr angeboten wird. b) Ein Betieb hat eine Kostenfunktion K(x) = 6x2 + 10x + 50 und kann dieses Produkt zum Marktpreis von 70 GE/ME verkaufen. - Berechnen Sie die langfristige Preisuntergrenze. - Berechnen Sie den maximalen Gewinn k = 6x + 10 + Error! Error! = 6 – Error! = 0 x = 2,89 ME LPU = k(2,89) = 45 GE/ME G(x) = 70x – 6x2 – 10x – 50 = –6x2 + 60x – 50 G‘(x) = 0 = –12x + 60 x = 5 G(5) = 100 GE 4. Lernzielkontrolle aus Mathematik und angewandter Mathematik 2 al – kirisits Mittwoch, 1. Juni 2016 Gruppe B ACHTUNG: Fehlerhafte und unübliche Notationen sind bewertungsrelevant und führen zu Punkteabzügen. Beantworten Sie Anwendungsbeispiele in ganzen Sätzen. Dokumentieren Sie Lösungswege (Ansätze, Nebenrechnungen, Überlegungen) 1. 2. a) - Argumentieren Sie mathematisch, warum die Funktionsgleichung einer Polynomfunktion mindestens 3. Grades sein muss, wenn es zwei Extremwerte gibt. Eine notwendige Bedingung für das Vorliegen eines Extremwertes ist das Verschwinden der 1. Ableitung an diesen Stellen. Daher muss die 1. Ableitung mindestens quadratisch sein, weil sie sonst keine zwei Lösungen haben kann. Die Originalfunktion daher mindestens kubisch (also vom Grad 3) sein b) - Begründen Sie mathematisch, warum der Funktionsgraph von f(x) = 7x 4 – 3x2 symmetrisch ist. Alle Hochzahlen sind ganzzahlig durch 2 teilbar, daher wird der Funktionswert, unabhängig vom Vorzeichen des Arguments immer den gleichen Wert haben, also f(x) = f(–x) . c) - Berechnen Sie die Koordinaten aller Wendepunkte und Extremwerte von y = x 2 e–0,2x. y‘ = (2x – 0,2x2) e–0,1x y“ = (0,04x2 – 0,8x + 2) e–0,1x E1 (0 / 0) E2 (10 / 13,5) W1 (2,93 / 4,78) W2 (17,07 / 9,59) a) - Geben Sie die Gleichung der Asymptote von y = Error!an. - Geben Sie die Polstelle an. y = 3x + 10 – Error! daher Asymptote: y = 3x + 10 und Pol bei x = 0 b) - Zeichnen Sie möglichst genau den Funktionsgraph mit den Eigenschaften: Nullstellen bei N1 (0 / 0), N2 (3 / 0), N3 (5 / 0) Extremwerte bei E1 (1,2 / 8,2) und E2 (4,1 / –4,1) Wendepunkt bei W (2,7 / 2,1) c) - Berechnen Sie die Parameter der Funktion f(x) = ax4 + bx2 die den Wendepunkt bei W (10 / – 200 000) hat. Error! = 4ax3 + 2bx Error! = 12ax2 + 2b 0 = 1 200 a + 2b und –200 000 = 10 000 a + 100 b a = 4 ∧ b = – 2 400 B 3. a) Ein Swimmingpool hat die Form eines Rechtecks mit zwei angesetzten Halbkreisen (siehe Skizze). Die Fläche soll 70 m2 betragen. - Berechnen Sie die Abmessungen x und r so, dass die Kosten für die Umrahmung möglichst klein werden, wenn die Rundungen doppelt so teuer wie die geraden Randstücke sind Z(x,r) = 2 · 2 r + 2x → Minimum mit 70 = r2 + 2rx x = Error! Z(r) = 4 r + 2 · Error! Error! = 4 – Error! – = 0 r = Error! = 2,73 m und r = 2,73 m und x = 8,56 m b) Zwei Punkte A und B sind mit einer Rohrleitung zu verbinden. Die Strecke AX kostet um 40 % mehr als die Strecke BX. - Berechnen Sie die Länge der Strecken AX und BX, damit die Verbindung kostenoptimal wird. a = 40 m, b = 80 m Z(x) = x + 1,4 (80 – x)2 + 402 39,18 4. a) Error! = 0 x = 40,82 m und AX = 57,15 m und BX = Die nebenstehende Grafik stellt die Angebots- und Nachfragefunktion eines Produktes dar. - Bestimmen Sie aus der Grafik den Gleichgewichtspreis. - Bestimmen Sie den Nachfrageüberhang für einen Preis, der um 25 % geringer als der Gleichgewichtspreis ist. - Interpretieren Sie die Nullstelle der Nachfragefunktion und die Achsenschnittpunkte mit der Preisachse. Gleichgewichtspreis = 2 154 EUR/ME Nachfrageüberhang bei p = 1 616 = 16,9 – 10,1 = 6,8 ME 25 ME ist die Sättigungsmenge, mehr wird nicht nachgefragt 5 000 EUR/ME ist prohibitiv, d.h. bei diesem Preis wird nichts nachgefragt 1 000 EUR/ME ist der Preis, bei dem nichts mehr angeboten wird. b) Ein Betieb hat eine Kostenfunktion K(x) = 60x2 + 100x + 500 und kann dieses Produkt zum Marktpreis von 700 GE/ME verkaufen. - Berechnen Sie die langfristige Preisuntergrenze. - Berechnen Sie den maximalen Gewinn k = 6x + 10 + Error! Error! = 6 – Error! = 0 x = 2,89 ME LPU = k(2,89) = 450 GE/ME G(x) = 70x – 6x2 – 10x – 50 = –6x2 + 60x – 50 G‘(x) = 0 = –12x + 60 x = 5 G(5) = 1 000 GE 4. Lernzielkontrolle aus Mathematik und angewandter Mathematik 2 al – kirisits Mittwoch, 1. Juni 2016 Gruppe A ACHTUNG: Fehlerhafte und unübliche Notationen sind bewertungsrelevant und führen zu Punkteabzügen. Beantworten Sie Anwendungsbeispiele in ganzen Sätzen. Dokumentieren Sie Lösungswege (Ansätze, Nebenrechnungen, Überlegungen) 1. a) - Argumentieren Sie mathematisch, warum die Funktionsgleichung einer Polynomfunktion mindestens 3. Grades sein muss, wenn ein Wendepunkt vorliegt. b) - Begründen Sie mathematisch, warum der Funktionsgraph von f(x) = 7x4 – 3x2 + x nicht symmetrisch ist. c) - Berechnen Sie die Koordinaten aller Wendepunkte und Extremwerte von y = x 2 e–0,1x. A 2. c) a) - Geben Sie die Gleichung der Asymptote von y = Error!an. - Geben Sie die Polstelle an. b) - Zeichnen Sie möglichst genau den Funktionsgraph mit den Eigenschaften: Nullstellen bei N1 (0 / 0), N2 (3 / 0), N3 (5 / 0) Extremwerte bei E1 (1,2 / 8,2) und E2 (4,1 / –4,1) Wendepunkt bei W (2,7 / 2,1) - Berechnen Sie die Parameter der Funktion f(x) = ax4 + bx2 die den Wendepunkt bei W (10 / – 200 000) hat. A 3. a) Ein Swimmingpool hat die Form eines Rechtecks mit zwei angesetzten Halbkreisen (siehe Skizze). Die Fläche soll 70 m2 betragen. - Berechnen Sie die Abmessungen x und r so, dass die Kosten für die Umrahmung möglichst klein werden, wenn die Rundungen doppelt so teuer wie die geraden Randstücke sind b) Zwei Punkte A und B sind mit einer Rohrleitung zu verbinden. Die Strecke AX kostet um 80 % mehr als die Strecke BX. - Berechnen Sie die Länge der Strecken AX und BX, damit die Verbindung kostenoptimal wird. a = 40 m, b = 80 m A 4. a) Die nebenstehende Grafik stellt die Angebots- und Nachfragefunktion eines Produktes dar. - Bestimmen Sie aus der Grafik den Gleichgewichtspreis. - Bestimmen Sie den Nachfrageüberhang für einen Preis, der um 25 % geringer als der Gleichgewichtspreis ist. - Interpretieren Sie die Nullstelle der Nachfragefunktion und die Achsenschnittpunkte mit der Preisachse. Zeichnen Sie Hilfslinien in die Grafik ein. b) Ein Betieb hat eine Kostenfunktion K(x) = 6x2 + 10x + 50 und kann dieses Produkt zum Marktpreis von 70 GE/ME verkaufen. - Berechnen Sie die langfristige Preisuntergrenze. - Berechnen Sie den maximalen Gewinn 4. Lernzielkontrolle aus Mathematik und angewandter Mathematik 2 al – kirisits Mittwoch, 1. Juni 2016 Gruppe B ACHTUNG: Fehlerhafte und unübliche Notationen sind bewertungsrelevant und führen zu Punkteabzügen. Beantworten Sie Anwendungsbeispiele in ganzen Sätzen. Dokumentieren Sie Lösungswege (Ansätze, Nebenrechnungen, Überlegungen) 1. a) - Argumentieren Sie mathematisch, warum die Funktionsgleichung einer Polynomfunktion mindestens 3. Grades sein muss, wenn es zwei Extremwerte gibt. b) - Begründen Sie mathematisch, warum der Funktionsgraph von f(x) = 7x 4 – 3x2 symmetrisch ist. c) - Berechnen Sie die Koordinaten aller Wendepunkte und Extremwerte von y = x2 e–0,2x. B 2. a) - Geben Sie die Gleichung der Asymptote von y = Error!an. - Geben Sie die Polstelle an. b) - Zeichnen Sie möglichst genau den Funktionsgraph mit den Eigenschaften: Nullstellen bei N1 (0 / 0), N2 (3 / 0), N3 (5 / 0) Extremwerte bei E1 (1,2 / 8,2) und E2 (4,1 / –4,1) Wendepunkt bei W (2,7 / 2,1) c) - Berechnen Sie die Parameter der Funktion f(x) = ax4 + bx2 , die den Wendepunkt bei W (10 / – 200 000) hat. B 3. a) Ein Swimmingpool hat die Form eines Rechtecks mit zwei angesetzten Halbkreisen (siehe Skizze). Die Fläche soll 70 m2 betragen. - Berechnen Sie die Abmessungen x und r so, dass die Kosten für die Umrahmung möglichst klein werden, wenn die Rundungen doppelt so teuer wie die geraden Randstücke sind b) Zwei Punkte A und B sind mit einer Rohrleitung zu verbinden. Die Strecke AX kostet um 40 % mehr als die Strecke BX. - Berechnen Sie die Länge der Strecken AX und BX, damit die Verbindung kostenoptimal wird. a = 40 m, b = 80 m B 4. a) Die nebenstehende Grafik stellt die Angebots- und Nachfragefunktion eines Produktes dar. - Bestimmen Sie aus der Grafik den Gleichgewichtspreis. - Bestimmen Sie den Nachfrageüberhang für einen Preis, der um 25 % geringer als der Gleichgewichtspreis ist. - Interpretieren Sie die Nullstelle der Nachfragefunktion und die Achsenschnittpunkte mit der Preisachse. Zeichnen Sie die Hilfslinien ein. b) Ein Betieb hat eine Kostenfunktion K(x) = 60x2 + 100x + 500 und kann dieses Produkt zum Marktpreis von 700 GE/ME verkaufen. - Berechnen Sie die langfristige Preisuntergrenze. - Berechnen Sie den maximalen Gewinn