Aufgabe zur Angebots,-und Nachfragefunktion (Kapitel 4)

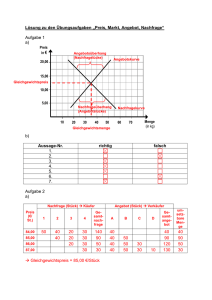
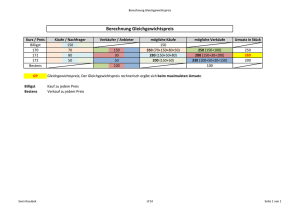
Aufgabe zur Angebots,-und Nachfragefunktion (Kapitel 4)
Für ein neues Smartphone welches einen Rasierer integriert hat und außerdem als
Flaschenöffner genutzt werden kann, sind folgende Angebots,- und Nachfragemengen
ermittelt worden:
Preis
5
6
7
8
9
10
Nachfragemenge Angebotsmenge
70
64
58
52
46
40
25
40
55
70
85
100
( Angaben in Tausend)
a) Zeichnen Sie , ausgehend von den vorhandenen Daten, die Angebotskurve (AT) und
die Nachfragekurve (NE).
Lösung=>
b) Versuchen Sie annähernd den Gleichgewichtspreis und die Gleichgewichtsmenge zu
ermitteln (zeichnerisch).
Lösung => durch ablesen:
=7
Antwort: Es ergibt sich ein Gleichgewichtspreis von 7000€ und eine Gleichgewichtsmenge
von 58000 Smartphones.
c) Es ergeben sich aus der Datenmenge folgende Geradengleichungen:
Nachfragefunktion:
Angebotsfunktion:
Bestimmen Sie nun algebraisch den Gleichgewichtspreis(
Gleichgewichtsmenge ( ).
) und die
Lösung=>
GG-Bedingungen:
( )
Durch einsetzten des errechneten Gleichgewichtspreises( ) in eine der beiden
Geradengleichungen erhält man die Gleichgewichtsmenge( ).
Oder
Antwort: Es ergibt sich ein Gleichgewichtspreis von7143€ und eine Gleichgewichtsmenge
von 57143 Smartphones.
d) Erläutern Sie wie sich Angebot und Nachfrage verhalten, wenn der Preis für ein
Smartphone 13000€ beträgt.
Lösung=>
Bei einem Preis von 13000€ ist die angebotene Menge größer als die nachgefragte Menge.
Es besteht dann ein Angebotsüberschuss. Der Lagerbestand der Smartphone-Anbieter
erhöht sich durch unverkaufte Exemplare. Es folgen Preissenkungen wodurch das Angebot
verringert wird und die Nachfrage erhöht wird. Das Ungleichgewicht behebt sich also selbst
durch die Wirkung von Angebot und Nachfrage.
e) Zusatzaufgabe für Mathematiker:
Beweisen Sie mit Hilfe der gegebenen Formel zur Ermittlung der Steigung einer
Geraden die durch zwei Punkte geht, dass die in Aufgabenteil c) gegeben
Steigungen der Nachfrage,- und der Angebotsfunktion korrekt sind.
(
und
)
( )
Lösung=>
Durch das Einsetzen von zwei beliebigen Punkten in die Steigungsgleichung kann die
Korrektheit der angegebenen Steigungen nachgewiesen werden.
Beispiel:
Punkte der Nachfragefunktion:
Daraus ergibt sich :
(70/5) und (40/10)
Punkte der Angebotsfunktion:
Daraus ergibt sich:
(100/10) und (25/5)