Name: 22 - Hartmut

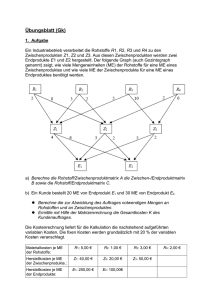
Name:
22.03.2012
Vorklausur Mathematik HHO
Folgende Hinweise zur Bearbeitung der Aufgaben: Die Lösungen sind doppelt
zu unterstreichen oder es ist ein Antwortsatz zu schreiben. Ergebnisse sind auf
zwei Nachkommastellen zu runden. Zeichnungen sind mit Bleistift durchzuführen.
Aufgabe1:
Die Kosten eines Sportartikelherstellers werden durch die ertragsgesetzliche Kostenfunktion K(x) = ax3 + bx2 + cx + d berechnet. Dabei geht der Hersteller von fixen
Kosten von 800 GE aus. Die Grenzkosten betragen bei einer Produktion von 8 ME
50 GE und bei einer Produktion von 3 ME 5 GE. Der Tiefpunkt der Grenzkosten liegt
bei einer Menge von 4 ME.
a) Berechnen Sie die Kostenfunktion und zeigen Sie, dass gilt:
K(x) = x3 – 12x2 + 50x + 800.
b) Bestimmen Sie das Intervall abnehmender und zunehmender Grenzkosten.
c) Berechnen Sie das Betriebsminimum sowie die kurzfristige Preisuntergrenze und
äußern Sie sich zu deren ökonomischer Bedeutung.
d) Der Hersteller behauptet, dass die langfristige Preisuntergrenze bei 110 GE/ME
liegt. Beurteilen Sie diese Behauptung.
Der Sportartikelhersteller hat in seinem Absatzgebiet eine gewisse Monopolstellung
und sieht sich mit einer Preisabsatzfunktion vom Typ pN(x) = -mx + b konfrontiert. Er
geht von einem Höchstpreis von 660 GE und einer Sättigungsmenge von 12 ME
aus.
e) Bestimmen Sie seine Preisabsatzfunktion und die dazugehörige Erlösfunktion.
Rechnen Sie im Folgenden mit der Erlösfunktion E(x) = - 55x2 + 660x.
f) Bestimmen Sie den maximalen Erlös.
g) Berechnen Sie die Gewinnzone.
h) Der Hersteller glaubt, dass bei einem Preis von 336,6 GE/ME der Gewinn maximal ist. Bestätigen oder widerlegen Sie diese Aussage.
i) Aufgrund eines guten Kostenmanagements fallen die fixen Kosten um 10 %. Begründen oder widerlegen Sie die Behauptung, dass sich die gewinnmaximale
Menge nicht ändert.
15.05.2016
Seite 1/5
j)
Im folgenden Koordinatensystem ist die Kostenfunktion eingezeichnet. Zeichnen
Sie die Erlös-, Gewinn- und Nachfragefunktion in dieses Koordinatensystem ein
und kennzeichnen Sie die wichtigen Punkte.
y




x





















15.05.2016
Seite 2/5
Aufgabe 2:
Der Sportartikelhersteller fertigt u.a.in einem zweistufigen Produktionsprozess auf der
ersten Stufe aus 3 Rohstoffen R1, R2 und R3 die 3 Zwischenprodukte Z1, Z2 und Z3
und aus denen dann schließlich die drei Endprodukte E 1, E2 und E3. Die folgenden
Matrizen RZ und ZE geben an, wieviele ME der verschiedenen Rohstoffe in einer ME
der Zwischenprodukte bzw. wieviele ME der verschiedenen Zwischenprodukte in
einer ME der Endprodukte vorhanden sind.
Z1 Z2
Z3
E1 E2 E3
RZ =
ZE =
a) Berechnen Sie die Matrix RE, die angibt, wie viele ME der Rohstoffe für je eine
ME der Endprodukte benötigt werden.
b) Berechnen Sie den Rohstoffverbrauch, wenn eine externe Bestellung von Endprodukten mit
= (150 200 250) vorliegt und das Lager 80 ME Z1, 50 ME Z2
und 120 ME Z3 bestellt.
Für die weitere Berechnung der Teilaufgaben benutzen Sie die folgende Rohstoffverbrauchsmatrix RE.
E1
E2
E3
RE =
c) Es liegt ein Kundenauftrag über 120 ME E1, 200 ME E2 und 150 ME E3 vor. Die
Rohstoffkosten je ME sind betragen 5 GE für R1, 3 GE für R2 und 2 GE für R3.
Berechnen Sie die Materialkosten für diesen Auftrag.
d) Für die nächste Rechnungsperiode gelten folgende Rohstoffstückkosten.
Rohstoffe
R1
R2
R3
GE/ME
6
2,5
4
Der Energie- und Arbeitseinsatz pro ME der Endprodukte ist durch die nachfolgende Tabelle gegeben.
15.05.2016
Seite 3/5
Endprodukte
E1
E2
E3
Energie
5
4
6
Arbeit
7
10
12
1 ME Energie kostet 9,5 GE und 1 ME Arbeit kostet 15 GE. Berechnen Sie die
Produktionskosten (Material-, Energie- und Arbeitskosten) bei einer Bestellung
von 300 ME E1, 400 ME E2 und 250 ME E3.
e) Die Endprodukte werden zu folgenden Preisen je ME verkauft: 550 GE bei E 1,
600 GE bei E2 und 850 GE bei E3. Der Hersteller rechnet mit einem Gewinn für
die Bestellung aus Teil d), wenn er mit fixen Kosten von 12.000 GE rechnet. Ist
dies realistisch?
15.05.2016
Seite 4/5
Aufgabe 3:
Bitte beachten Sie, dass bei allen Berechnungen von den Grundformeln ausgegangen werden muss. Tabellarische Lösungen werden nicht anerkannt. Bei
schon fertig umgestellten Formeln werden die Punkte für das Umstellen der
Grundformeln nicht anerkannt.
a) Die Hausbank des Sportartikelherstellers ist bereit, für ein vor 8 Jahren festgelegtes Kapital von 145.000 € einen Betrag von 202.290,98 € auszuzahlen. Mit welchem Zinssatz hat die Bank gerechnet?
b) Der Sportartikelhersteller will ein Grundstück kaufen, um dort eine neue Lagerhalle zu bauen. Der Verkäufer des Grundstücks unterbreitet ihm drei Angebote:
Angebot 1: 100.000 € sofort und 300.000 € nach 6 Jahren
Angebot 2: 50.000€ sofort, 100.000 € nach 3 Jahren und 250.000 € nach
7 Jahren
Angebot 3: 80.000 € alle zwei Jahre 3-mal am Anfang des Jahres
Welches Angebot ist für den Hersteller am günstigsten, wenn er mit 4,5 % Zinsen
rechnet?
c) Der Hersteller rechnet damit, dass in einigen Jahren eine Erweiterungsinvestition
in Höhe von 240.000 € notwendig ist. Nach wie vielen Jahren steht dieser Betrag
zur Verfügung, wenn er jeweils am Ende des Jahres 36.000 € zu 4,5 % anlegt?
d) Um das Ansehen des Unternehmens zu vergrößern, plant die Geschäftsleitung
des Sportartikelherstellers in den nächsten 10 Jahre jährlich 100 Sportler am Anfang des Jahres mit einem Betrag von jeweils 12.000 € zu unterstützen. Welchen
Einmalbetrag muss das Unternehmen am Anfang der ersten Zahlung auf einem
Konto bei 4 % Zinssatz angelegt haben, um alle anfallenden Zahlungen leisten
zu können?
e) Die Geschäftsleitung hat angeregt, einen Fonds in Höhe von 350.000 € zu 5 %
Zinssatz anzulegen, um aus diesem für die nächsten 8 Jahre jährlich am Ende
des Jahres einen festen Betrag für Verbesserungsvorschläge der Mitarbeiter zu
entnehmen. Welcher Betrag steht jährlich zur Verfügung, wenn der Fond nach 8
Jahren verteilt sein soll?
15.05.2016
Seite 5/5