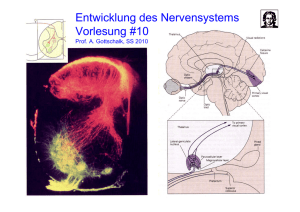
¤Info Kleines Computer-Lexikon (wird von LETRA98 benutzt
Werbung

¤Info Kleines Computer-Lexikon (wird von LETRA98 benutzt) Geometrie Sekundarstufe I © by J. Widmer, ATEUS 98 Zweck: Nachschlagen von unbekannten Begriffen Repetition und Prüfungsvorbereitung Vernetzen des Lernstoffes durch "Surfen" im Lexikon ¤Achsenspiegelung auch Geradenspiegelung, eine Kongruenzabbildung s.a Achsenspiegelung_Film Eigenschaften: 1. Originalfigur und Bildfigur haben gleiche Gestalt und Grösse, sie sind deckungsgleich. Daraus folgt: - die Länge einer Strecke bleibt erhalten - die Grösse eines Winkels bleibt erhalten - parallele Geraden bleiben parallel 2. Achsensymmetrische Punkte haben gleichen Abstand von der Symmetrieachse. Punkte auf der Symmetrieachse fallen mit ihrem Bildpunkt zusammen. 3. Die Verbindungsgerade achsensymmetrischer Punkte steht rechtwinklig zur Symmetrieachse (= Mittelsenkrechte). 4. Achsensymmetrische Geraden sind parallel zur Symmetrieachse oder schneiden sich auf der Achse und bilden mit ihr gleich grosse Winkel (= Mittelparallele bzw. Winkelhalbierende) 5. Originalfigur und Bildfigur haben den gleichen Umlaufsinn. 6. Eine Achsenspiegelung (Geradenspiegelung) ist durch die Spiegelachse (Symmetrieachse) eindeutig festgelegt. BILDpict/spiegel.bmp ¤Achsenspiegelung_Film s.a. Achsenspiegelung BILDpict/achsensp.avi ¤Aehnlichkeitssätze Dreiecke sind ähnlich, wenn sie in zwei entsprechenden Winkeln übereinstimmen.(ww) Dreiecke sind ähnlich, wenn sie im Verhältnis zweier Seiten und dem von ihnen eingeschlossenen Winkel übereinstimmen.(sws) Dreiecke sind ähnlich, wenn sie im Verhältnis zweier Seiten und dem der grösseren Seite gegenüberliegenden Winkel übereinstimmen.(ssW) Dreiecke sind ähnlich, wenn sie im Verhältnis der drei Seiten übereinstimmen. (sss) ¤Aussenwinkel Ein Aussenwinkel am Dreieck ist gleich der Summe der nicht anliegenden Innenwinkel BILDpict/aussenwi.bmp ¤Basiswinkel Im gleichschenkligen Dreieck gilt: Basiswinkel sind gleich gross. BILDpict/basisw.bmp ¤Berührungsradius Der Berührungsradius steht rechtwinklig zur Tangenten. BILDpict/kreis2.bmp ¤Bogen Es gilt die Proportion: Bogen : Umfang = Zentriwinkel : 360° BILDpict/bogen.bmp ¤Drachenviereck auch Deltoid - es hat eine Symmetrieachse - die Diagonalen stehen rechtwinklig zueinander e·f A = ————— 2 BILDpict/drachenv.bmp Fläche: ¤Drehung auch Rotation, eine Kongruenzabbildung s.a Drehung_Film Eigenschaften: 1. Jeder Punkt der Originalfigur bewegt sich - um den gleichen Drehwinkel - im gleichen Drehsinn - auf einem Kreis um das Drehzentrum 2. Originalfigur und Bildfigur haben gleiche Gestalt und Grösse, sie sind deckungsgleich. Daraus folgt: - die Länge einer Strecke bleibt erhalten - die Grösse eines Winkels bleibt erhalten - parallele Geraden bleiben parallel 3. Die Verbindungsstrecken entsprechender Punkte mit dem Drehzentrum bilden gleiche Winkel (= Drehwinkel). 4. Originalfigur und Bildfigur haben den gleichen Umlaufsinn. 5. Eine Drehung ist durch das Drehzentrum, den Drehwinkel und den Drehsinn eindeutig festgelegt. BILDpict/rotation.bmp ¤Drehung_Film s.a. Drehung BILDpict/drehung.avi ¤Dreieck Grundlinie mal Höhe Fläche des Dreiecks = ——————————————————— 2 g·h A = ——— 2 BILDpict/dreieck.bmp ¤Flächenverhältnis Das Verhältnis der Flächen zweier ähnlicher Figuren ist gleich dem Quadrat des Streckungsfaktors: 2 A' : A = k BILDpict/aehnl1.bmp ¤Flächenverwandlung Dreieck auch Scherung Solange die Grundlinie g und die zugehörige Höhe h im Dreieck gleich bleiben, bleibt die Dreiecksfläche gleich. BILDpict/scherdre.avi ¤Flächenverwandlung Parallelogramm auch Scherung Solange die Grundlinie g und die zugehörige Höhe h im Rhomboid gleich bleiben, bleibt die Fläche gleich. BILDpict/scherpar.avi ¤Gegenwinkel Gegenwinkel an Parallelen messen zusammen 180 Grad BILDpict/gegenwin.bmp ¤Geradenspiegelung eine Kongruenzabbildung, siehe Achsenspiegelung BILDpict/spiegel.bmp ¤g.O. geometrischer Ort, geometrische Örter, Ortslinien Linien, deren Punkte bestimmte Bedingungen erfüllen, heissen geometrische Örter. Beispiele: Der g.O. aller Punkte, die von einem Punkt gleich weit entfernt sind, ist der Kreis. Der g.O. aller Punkte die von 2 Punkten die gleiche Entfernung haben, ist die Mittelsenkrechte. Der g.O. aller Punkte, die von 2 parallelen Geraden den gleichen Abstand haben, ist die Mittelparallele. Der g.O. aller Punkte, die von einer Geraden den gleichen Abstand haben, ist das Parallelenpaar. Der g.O. aller Punkte, die von zwei sich schneidenden Geradenb den gleichen Abstand haben, ist das Winkelhalbierendenpaar. Der g.O. aller Punkte, von denen aus eine Strecke unter dem gleichen Winkel erscheint, ist das Ortsbogenpaar. ¤geometrischer Ort s. g.O. ¤gleichliegende Winkel Gleichliegende Winkel (auch Stufenwinkel) an Parallelen sind gleich gross BILDpict/stufenwi.bmp ¤Höhensatz s.a. Höhensatz_Film Höhensatz des Euklid: Im rechtwinkligen Dreieck ist das Quadrat über der Höhe flächengleich dem Rechteck aus den Hypotenusenabschnitten. 2 h = pq BILDpict/hoehens1.bmp ¤Höhensatz_Film s.a. Höhensatz BILDpict/hoehens.avi ¤Hypotenuse Die längste Seite im rechtwinkligen Dreieck. ¤Hypotenusenabschnitte Im rechtwinkligen Dreieck teilt der Fusspunkt der Höhe zur Hypotenuse diese in die beiden Hypotenusenabschnitte. (im Bild p und q) BILDpict/hoehens1.bmp ¤Inkreismittelpunkt Die Winkelhalbierenden im Dreieck schneiden sich im Inkreismittelpunkt. BILDpict/inkreism.bmp ¤Innenwinkel Die Summe der Innenwinkel im Dreieck beträgt 180°. Die Summe der Innenwinkel im Viereck beträgt 360°. ¤Kathete Die beiden kürzeren Seiten im rechtwinkligen Dreieck heissen Katheten. ¤Kathetensatz Kathetensatz des Euklid s.a. Kathetensatz_Film Im rechtwinkligen Dreieck ist das Quadrat über einer Kathete flächengleich dem Rechteck, gebildet aus der Hypotenuse und dem anliegenden Hypotenusenabschnitt. BILDpict/katheten.bmp ¤Kathetensatz_Film s.a. Kathetensatz, Pythagoras BILDpict/katheten.avi ¤Kongruenzsätze Dreiecke sind kongruent, wenn sie in drei Seiten übereinstimmen. (sss) Dreiecke sind kongruent, wenn sie in zwei Seiten und dem von ihnen eingeschlossenen Winkel übereinstimmen. (sws) Dreiecke sind kongruent, wenn sie in einer Seite und den beiden anliegenden Winkeln übereinstimmen. (wsw) Dreiecke sind kongruent, wenn sie in zwei Seiten und dem der grösseren Seite gegenüberliegenden Winkel übereinstimmen. (ssW) ¤Kreis Bezeichnungen: 1 2 3 4 5 6 Sehne Sekante Durchmesser Zentrale (Berührungs-)radius Tangente Berechnung: u = 2r 7 8 9 10 11 Peripherie (Kreisrand) Peripheriewinkel Zentriwinkel Sektor(-fläche) Segment A = r² BILDpict/kreisbez.bmp ¤Mittelparallele im Dreieck Sie halbiert zwei Dreiecksseiten und liegt parallel zur dritten Seite. BILDpict/mittelpa.bmp ¤Nebenwinkel Nebenwinkel messen zusammen 180 Grad. BILDpict/nebenwin.bmp ¤Ortsbogen Der geometrische Ort aller Punkte, von denen aus eine gegebene Strecke unter einem gegebenen Winkel erscheint, ist das Ortsbogenpaar. Alle Peripheriewinkel über der gleichen Sehne (bzw. über dem gleichen Bogen) sind gleich gross. Jeder Peripheriewinkel ist halb so gross wie der zugehörige Zentriwinkel. BILDpict/ortsboge.bmp ¤Parallelogramm s. Rhomboid, Rhombus, Rechteck, Quadrat ¤Parallelverschiebung auch Translation, eine Kongruenzabbildung s.a. Parallelverschiebung_Film Eigenschaften: 1. Jeder Punkt der Originalfigur bewegt sich - um die gleiche Strecke - in der gleichen Richtung - auf einer Geraden, die zu den andern Verschiebungsgeraden parallel ist 2. Originalfigur und Bildfigur haben gleiche Gestalt und Grösse, sie sind deckungsgleich. Daraus folgt: - die Länge einer Strecke bleibt erhalten - die Grösse eines Winkels bleibt erhalten - parallele Geraden bleiben parallel 3. Eine in der Verschiebungsrichtung liegende Gerade wird in sich selbst verschoben, jede andere Gerade geht in eine entsprechende parallele Gerade über. 4. Originalfigur und Bildfigur haben den gleichen Umlaufsinn. 5. Eine Parallelverschiebung ist durch einen Schiebungspfeil (Vektor) eindeutig festgelegt. BILDpict/translat.bmp ¤Parallelverschiebung_Film s.a. Parallelverschiebung BILDpict/parallel.avi ¤Peripherie s. Kreis ¤Peripheriewinkel s.a. Peripheriewinkel_Film Sie haben ihren Scheitelpunkt auf der Peripherie eines Kreises. Ihre Schenkel schneiden die Peripherie (den Kreis) Alle Peripheriewinkel über der gleichen Sehne (bzw. über dem gleichen Bogen) sind gleich gross. Jeder Peripheriewinkel ist halb so gross wie der zugehörige Zentriwinkel. BILDpict/peripher.bmp ¤Peripheriewinkel_Film s.a. Peripheriewinkel BILDpict/periwin.avi ¤Prisma BILDpict/prisma.bmp ¤Proportion Eine Proportion ist die Gleichsetzung zweier Verhältnisse (auch Verhältnisgleichung oder Quotientengleichung): z.B.: a : b = c : x Es gilt: a : b = c : x <=> ax = bc (Kreuzprodukt,Produktengleichung) ————————————— ——————— x wird "4. Proportionale" genannt: x = bc : a Spezialfall: die stetige Proportion 2 a : x = x : b <=> x = ab x wird "mittlere Proportionale" genannt: x = Wurzel aus ab ¤Punktspiegelung auch Drehung um 180 Grad, eine Kongruenzabbildung s.a. Punktspiegelung_Film Eigenschaften: 1. Jeder Punkt der Originalfigur bewegt sich - um 180 Grad - auf einem Kreis um das Drehzentrum 2. Originalfigur und Bildfigur haben gleiche Gestalt und Grösse, sie sind deckungsgleich. Daraus folgt: - die Länge einer Strecke bleibt erhalten - die Grösse eines Winkels bleibt erhalten - parallele Geraden bleiben parallel 3. Punktsymmetrische Punkte liegen gleich weit vom Symmetriezentrum entfernt. 4. Die Verbindungsstrecke punktsymmetrischer Punkte geht durch das Symmetriezentrum. 5. Punktsymmetrische Geraden sind parallel oder liegen auf einer Geraden, die durch das Symmetriezentrum geht. 6. Originalfigur und Bildfigur haben den gleichen Umlaufsinn. 7. Eine Drehung ist durch das Drehzentrum (Symmetriezentrum) eindeutig festgelegt. BILDpict/punktspi.bmp ¤Punktspiegelung_Film s.a. Punktspiegelung BILDpict/punktsp.avi ¤Pyramide A·h V = ————— 3 (A = Grundfläche) BILDpict/pyramide.bmp ¤Pythagoras Im rechwinkligen Dreieck gilt: Das Hypotenusenquadrat ist gleich der Summe aus den beiden Kathetenquadraten. 2 a 2 + b 2 = c s.a. Kathetensatz, Kathetensatz_Film BILDpict/pythagor.bmp ¤Quader V = l·b·h BILDpict/quader.bmp ¤Quadrat spezielles Parallelogramm Seitenlängen: Gegenseiten: Summe der Eckwinkel: gegenüberliegende Winkel: Länge der Diagonalen: Diagonalenabschnitte: Diagonalenwinkel: Eckwinkel: Symmetrieachsen: Symmetriezentrum: Inkreis: Umkreis: alle vier gleich lang gleich lang, parallel 360 Grad gleich gross, 90 Grad gleich lang alle gleich lang je 90 Grad 90 Grad, werden halbiert 4: Diagonalen, Mittellinien Diagonalenschnittpunkt ja ja BILDpict/quadrat.bmp ¤Rechteck spezielles Parallelogramm Seitenlängen: Gegenseiten: Summe der Eckwinkel: gegenüberliegende Winkel: Länge der Diagonalen: Diagonalenabschnitte: Diagonalenwinkel: Eckwinkel: Symmetrieachsen: Symmetriezentrum: Inkreis: Umkreis: je zwei gleich lang gleich lang, parallel 360 Grad gleich gross gleich lang alle gleich lang nicht 90 Grad werden nicht halbiert 2: Mittellinien Diagonalenschnittpunkt nein ja ¤Rechtwinkliges Dreieck Die beiden kleineren Seiten heissen Katheten, die grösste Hypotenuse. Es gilt der Satz des Pythagoras: Das Hypotenusenquadrat ist gleich der Summe aus den Kathetenquadraten. 2 a 2 + b 2 = c Der Umkreis des rechtwinkligen Dreiecks ist der Thaleskreis. BILDpict/redrei1.bmp ¤Rhomboid allgemeines Parallelogramm Seitenlängen: Gegenseiten: Summe der Eckwinkel: gegenüberliegende Winkel: je zwei gleich lang gleich lang, parallel 360 Grad gleich gross Länge der Diagonalen: Diagonalenabschnitte: Diagonalenwinkel: Eckwinkel: Symmetrieachsen: Symmetriezentrum: Inkreis: Umkreis: nicht gleich lang je zwei gleich lang nicht 90 Grad werden nicht halbiert keine Diagonalenschnittpunkt nein nein BILDpict/rhomboid.bmp ¤Rhombus spezielles Parallelogramm Seitenlängen: Gegenseiten: Summe der Eckwinkel: gegenüberliegende Winkel: Länge der Diagonalen: Diagonalenabschnitte: Diagonalenwinkel: Eckwinkel: Symmetrieachsen: Symmetriezentrum: Inkreis: Umkreis: alle vier gleich lang gleichlang, parallel 360 Grad gleich gross nicht gleich lang je zwei gleich lang 90 Grad werden halbiert 2: Diagonalen Diagonalenschnittpunkt ja nein BILDpict/rhombus.bmp ¤Rotation auch Drehung, eine Kongruenzabbildung BILDpict/rotation.bmp ¤Scheitelpunkt Schnittpunkt der Schenkel eines Winkels ¤Scheitelwinkel Scheitelwinkel sind gleich gross. BILDpict/scheitel.bmp ¤Schwerpunkt Die Seitenhalbierenden (Schwerlinien) im Dreieck schneiden sich im Schwerpunkt. Der Schwerpunkt teilt die Seitenhalbierenden im Verhältnis 1 : 2 BILDpict/schwerpu.bmp ¤Segment s. Kreis ¤Sehnen Gleichlange Sehnen im gleichen Kreis haben gleiche Abstände von Zentrum. BILDpict/sehnen.bmp ¤Sehnenviereck Gegenüberliegende Winkel im Sehnenviereck messen zusammen 180°. BILDpict/sehnenvier.bmp ¤Seitenhalbierende Die Seitenhalbierenden (Schwerlinien) im Dreieck schneiden sich im Schwerpunkt. Sie teilen sich im Verhältnis 1 : 2 BILDpict/schwerpu.bmp ¤Sektor Für die Sektorfläche (A) gelten die Proportionen: Sektorfläche : Kreisfläche = Bogen : Umfang und Sektorfläche : Kreisfläche = Zentriwinkel : 360 Grad Es gilt auch: A = b·r : 2 s.a. Kreis BILDpict/sektor.bmp ¤Spiegelung siehe Punktspiegelung oder Achsenspiegelung ¤Strahlensatz 1 Erster Strahlensatz: Werden die Schenkel eines Winkels von parallelen Geraden geschnitten, so verhalten sich die Abschnitte auf dem einen Schenkel wie die entsprechenden Abschnitte auf dem andern Schenkel. BILDpict/strahl1.bmp ¤Strahlensatz 2 Zweiter Strahlensatz: Werden die Schenkel eines Winkels von parallelen Geraden geschnitten, so verhalten sich die Abschnitte auf den Parallelen wie die Abschnitte auf einem Schenkel vom Scheitelpunkt aus gemessen. ————— BILDpict/strahl2.bmp ¤Streckung siehe zentrische Streckung ¤Streckungsfaktor auch Aehnlichkeitsverhältnis bei ähnlichen Figuren gilt für den Streckungsfaktor k: k = Bildstrecke : entsprechender Originalstrecke k<1 k=1 k>1 —> Verkleinerung —> Original- und Bildfigur sind kongruent —> Vergrösserung Flächenverhältnis: Das Verhältnis der Flächen zweier ähnlicher Figuren ist gleich dem Quadrat des Streckungsfaktors: 2 A' : A = k BILDpict/aehnl1.bmp ¤Stufenwinkel Stufenwinkel (auch gleichliegende Winkel) an Parallelen sind gleich gross BILDpict/stufenwi.bmp ¤Symmetrieachse auch Spiegelachse, siehe Achsenspiegelung BILDpict/spiegel.bmp ¤Symmetriezentrum Drehzentrum einer Drehung um 180 Grad (Punktspiegelung) BILDpict/punktspi.bmp ¤Tangente Tangenten (t) stehen rechtwinklig zum Berührungsradius.(r) BILDpict/kreis2.bmp ¤Tangenten an Kreis Tangenten stehen rechtwinklig zum Berührungsradius. BILDpict/tangente.bmp ¤Translation auch Parallelverschiebung, eine Kongruenzabbildung BILDpict/translat.bmp ¤Trapez Viereck, bei dem zwei gegenüberliegende Seiten parallel sind BILDpict/trapez.bmp ¤Umkreismittelpunkt Die Mittelsenkrechten zu den Dreiecksseiten schneiden sich im Umkreismittelpunkt. BILDpict/umkreism.bmp ¤Verhältnis Unter dem Verhältnis zweier Grössen versteht man den Quotienten ihrer Masszahlen. Beispiel: Eine Strecke a misst 6cm, eine Strecke b 4cm. Ihr Verhältnis (a : b) ist 6cm : 4cm = 6 : 4 = 3 : 2 = 1,5 : 1 = 1,5 ¤Wechselwinkel Wechselwinkel an Parallelen sind gleich gross. BILDpict/wechselw.bmp ¤Winkelhalbierende Die Winkelhalbierenden im Dreieck schneiden sich im Inkreismittelpunkt. Die Winkelhalbierende teilt eine Dreiecksseite im Verhältnis der anliegenden Seiten: u : v = b : a BILDpict/winkelha.bmp ¤Winkel halbieren Konstruktion (Film) BILDpict/winkelhalb.avi ¤Würfel V = s³ O = 6s² BILDpict/wuerfel.bmp ¤zentrische Streckung Unter einer zentrischen Streckung mit dem Zentrum Z und dem Streckungsfaktor k verstehen wir eine punktweise Abbildung nach folgender Vorschrift: 1. Jeder von Z verschiedene Punkt A wird in den Bildpunkt A' abgebildet, dass gilt: ___ __ A'Z : AZ = k (Streckungsverhältnis) A, Z und A' liegen auf der gleichen Geraden 2. Das Zentrum Z wird auf sich selbst abgebildet: Z=Z' Eigenschaften zentrisch gestreckter Figuren: - sie sind ähnlich (winkeltreu und verhältnistreu) - Geraden durch Z werden auf sich selbst abgebildet, jede andere Gerade wird in eine zu ihr parallelen Gerade abgebildet - der Umlaufsinn von Original- und Bildfigur ist gleich Zum Beispiel im Bild: Streckungsverhältnis: k = a' : a = b' : b = c' : c = 5 : 2 = 2,5 (d.h. jede Bildstrecke ist 2,5 mal so lang wie ihre entsprechende Originalstrecke) Flächenverhältnis: k² = A' : A = 25 : 4 = 6,25 (Beispiel) (d.h. die Bildfläche ist 6,25 mal so gross wie die Originalfläche) BILDpict/zstreck1.bmp ¤zentrische Streckung (Film) s.a. zentrische Streckung BILDpict/streckg.avi ¤Zentriwinkel Er hat seinen Scheitelpunkt im Zentrum eines Kreises. Jeder Peripheriewinkel ist halb so gross wie der zugehörige Zentriwinkel. BILDpict/zentriw.bmp ¤Zylinder d² V = ————— · h 4 d² O = ————— + dh 2 (dh = Mantel) BILDpict/zylinder.bmp