Grundwissensaufgaben 10. Jgst

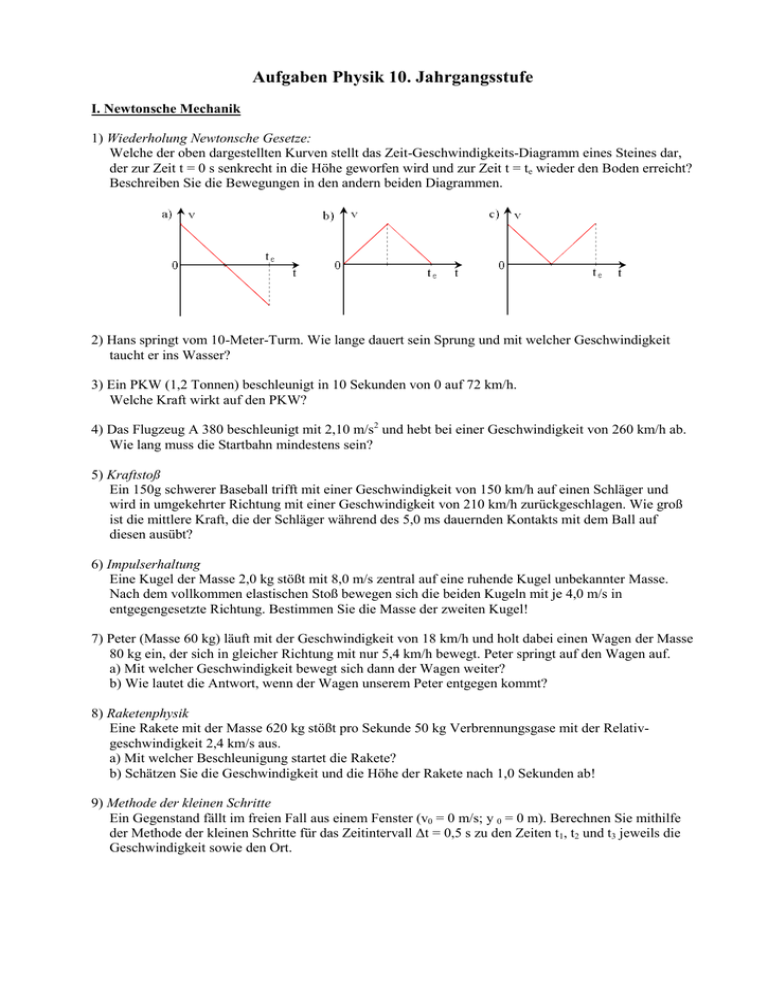
Aufgaben Physik 10. Jahrgangsstufe
I. Newtonsche Mechanik
1) Wiederholung Newtonsche Gesetze:
Welche der oben dargestellten Kurven stellt das Zeit-Geschwindigkeits-Diagramm eines Steines dar,
der zur Zeit t = 0 s senkrecht in die Höhe geworfen wird und zur Zeit t = te wieder den Boden erreicht?
Beschreiben Sie die Bewegungen in den andern beiden Diagrammen.
2) Hans springt vom 10-Meter-Turm. Wie lange dauert sein Sprung und mit welcher Geschwindigkeit
taucht er ins Wasser?
3) Ein PKW (1,2 Tonnen) beschleunigt in 10 Sekunden von 0 auf 72 km/h.
Welche Kraft wirkt auf den PKW?
4) Das Flugzeug A 380 beschleunigt mit 2,10 m/s2 und hebt bei einer Geschwindigkeit von 260 km/h ab.
Wie lang muss die Startbahn mindestens sein?
5) Kraftstoß
Ein 150g schwerer Baseball trifft mit einer Geschwindigkeit von 150 km/h auf einen Schläger und
wird in umgekehrter Richtung mit einer Geschwindigkeit von 210 km/h zurückgeschlagen. Wie groß
ist die mittlere Kraft, die der Schläger während des 5,0 ms dauernden Kontakts mit dem Ball auf
diesen ausübt?
6) Impulserhaltung
Eine Kugel der Masse 2,0 kg stößt mit 8,0 m/s zentral auf eine ruhende Kugel unbekannter Masse.
Nach dem vollkommen elastischen Stoß bewegen sich die beiden Kugeln mit je 4,0 m/s in
entgegengesetzte Richtung. Bestimmen Sie die Masse der zweiten Kugel!
7) Peter (Masse 60 kg) läuft mit der Geschwindigkeit von 18 km/h und holt dabei einen Wagen der Masse
80 kg ein, der sich in gleicher Richtung mit nur 5,4 km/h bewegt. Peter springt auf den Wagen auf.
a) Mit welcher Geschwindigkeit bewegt sich dann der Wagen weiter?
b) Wie lautet die Antwort, wenn der Wagen unserem Peter entgegen kommt?
8) Raketenphysik
Eine Rakete mit der Masse 620 kg stößt pro Sekunde 50 kg Verbrennungsgase mit der Relativgeschwindigkeit 2,4 km/s aus.
a) Mit welcher Beschleunigung startet die Rakete?
b) Schätzen Sie die Geschwindigkeit und die Höhe der Rakete nach 1,0 Sekunden ab!
9) Methode der kleinen Schritte
Ein Gegenstand fällt im freien Fall aus einem Fenster (v0 = 0 m/s; y 0 = 0 m). Berechnen Sie mithilfe
der Methode der kleinen Schritte für das Zeitintervall Δt = 0,5 s zu den Zeiten t1, t2 und t3 jeweils die
Geschwindigkeit sowie den Ort.
10) Schwingungen
Sabine und ihr kleiner Bruder Claudius sind auf den Spielplatz zum Schaukeln gegangen. Sabine
schaukelt. Claudius ruft: „He, ich kann viel schneller hin und her schaukeln als du.“ „Glaub´ ich nicht,
du bist doch viel leichter als ich!“ antwortet Sabine. „Deswegen wirst du langsamer schaukeln.“ Wer
hat Recht? Was passiert, wenn beide Kinder zusammen auf der einen Schaukel schaukeln?
11) An einer Feder der Federhärte 20 N/m hängt eine Kugel der Masse 100 g. Die Kugel wird um 10 cm
nach unten ausgelenkt und dann losgelassen. Reibungseffekte sollen vernachlässigt werden.
a) Berechnen Sie die Schwingungsdauer der auftretenden harmonischen Schwingung. Geben Sie für
die Kugel die Ortsfunktion x(t) an und zeichnen Sie das t-x-Diagramm.
b) Bestimmen Sie die maximale Geschwindigkeit und die maximale Beschleunigung der Kugel und
geben Sie dann die Geschwindigkeit v(t) und die Beschleunigung a(t) der Kugel in Abhängigkeit
von der Zeit an.
12) Ein Kronleuchter der Masse 35 kg hängt an einem Seil der Länge l.
a) Wird der Kronleuchter in Schwingung versetzt, so pendelt er mit einer Schwingungsdauer von 2,7s.
Bestimmen Sie die Seillänge l.
b) An den Kronleuchter wird eine 10 kg schwere Kristallkugel angehängt. Wie ändert sich dadurch die
Schwingungsdauer?
13) Waagrechter Wurf
Stuntman James soll einen 30m breiten Fluss mit seinem
Sportwagen „überspringen“. Der Höhenunterschied der
beiden Uferseiten beträgt 12m. Mit welcher
Geschwindigkeit sollte James seinen Sprung wagen?
14) Kreisbewegung
Ein PKW (1,2 t) durchfährt mit einer Geschwindigkeit von 72 km/h auf waagrechter Strecke eine
Kurve mit dem Radius 60 m.
a) Wie groß ist die dafür benötigte Zentripetalkraft? Geben Sie diese Kraft auch in Vielfachen der
Gewichtskraft FG an.
b) Wer liefert diese Zentripetalkraft?
15) Gravitationsgesetz
Bestimmen Sie mit dem Sonnenradius und der Sonnenmasse die Fallbeschleunigung auf der
Sonnenoberfläche. Drücken Sie diese auch als Vielfaches von gErde aus.
II. Wellen und Quanten
1) Ausbreitung einer Welle:
Der Kammerton ist der gemeinsame Ton (sinusförmige Schallschwingung), auf den eine Gruppe von
Instrumenten eingestimmt wird. Als Standard-Kammerton wurde der Ton mit der Frequenz f = 440 Hz
(Kammerton a1) festgelegt. Welche Wellenlänge gehört zum Kammerton a1, wenn sich Schall mit der
Geschwindigkeit von etwa 340 m/s ausbreitet?
2) Ultraschall und Infraschall:
Schall oberhalb von 20 kHz heißt Ultraschall, Schall unterhalb von 16 Hz heißt Infraschall. Welche
Wellenlängen gehören zu Ultra- bzw. Infraschall? (cSchall ≈ 340 m/s)
3) Tsunami:
Für die Ausbreitungsgeschwindigkeit eines Tsunamis gilt: c=√g∙h , wobei g die Erdbeschleunigung
und h die Wassertiefe angibt. Für die Wellenlänge gilt näherungsweise λ≈h∙2π .
a) Welche Ausbreitungsgeschwindigkeit und welche Wellenlänge hat ein Tsunami im Pazifik mit
einer mittleren Meerestiefe von ca. 6 km?
b) Wie lange benötigt damit ein Tsunami von Japan nach San Francisco (ca. 8000 km)?
c) Wie ändern sich die Ausbreitungsgeschwindigkeit und die Wellenlänge, wenn die Wassertiefe von
6 km auf 500 m sinkt?
4) Interferenz:
Zwei Lautsprecher L1 und L2 senden gleichphasig
eine Schallwelle der Wellenlänge l = 0,40m aus.
Die Lautsprecher sind b = 1,60m voneinander entfernt.
a) Berechnen Sie die Frequenz der Schallwellen.
b) Zeigen Sie, dass am Punkt A konstruktive
Überlagerung stattfindet, d.h., dass man am
Punkt A den Ton sehr laut wahrnimmt.
c) Gibt es Punkte B und C so, dass man bei B
den Ton nur sehr leise, bei C dagegen den Ton
wieder sehr laut wahrnimmt? Berechnen Sie
gegebenenfalls die Abstände dieser Punkte von L2.
d) Begründen Sie, dass für einen Punkt P nur der so genannte Gangunterschied ∆s=x2 -x1 entscheidet,
ob man den Ton laut oder leise hört.
5) Einfachspalt
Licht der Wellenlänge 532 nm wird an einem Einfachspalt gebeugt. Auf dem 60 cm hinter dem Spalt
aufgestellten Schirm beobachtet man das abgebildete Interferenzmuster. Die beiden Minima erster
Ordnung haben einen Abstand von 2,1 cm. Berechnen Sie die Spaltbreite.
6) Gitter
Laserlicht der Wellenlänge 670 nm trifft senkrecht auf ein Gitter mit 400 Strichen pro Millimeter. Im
Abstand d = 50cm befindet sich ein Schirm. Berechnen Sie den Abstand x, den die beiden Lichtpunkte
1. Ordnung voneinander haben.
7) Photonen
Erklären Sie den Begriff Photon
8.) Elektromagnetisches Spektrum
Ordnen Sie die Begriffe so, dass die Strahlungsenergie zunimmt!
UV-Strahlung, Mikrowellen, sichtbares Licht, Radiowellen, γ-Strahlung, Infrarotstrahlung,
Röntgenstrahlung
9.) Doppelspalt
Welche überraschende Deutung erzwingt der Doppelspaltversuch mit Elektronen?