Unmögliche Figuren – perspektivisches Zeichnen: Kompetenzen

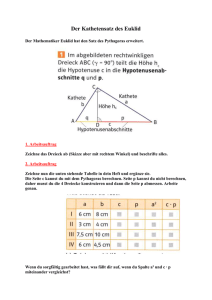
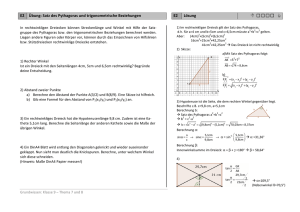
Unmögliche Figuren – perspektivisches Zeichnen:
Kompetenzen:
Die Schüler/innen sollen
●
Ein quaderförmiges Werkstück in der Schrägbildperspektive darstellen und bemaßen
können.
●
Ein Werkstück mit veränderter Vorderfläche darstellen können
●
Konstruktionen auf einen unlinierten Papier sauber durchführen können.
●
Nach Konstruktionsanweisungen arbeiten können
●
Eine Fluchtpunktkonstruktion ohne Bemaßungen durchführen können.
●
Den Begriff Prisma kennen und auf Netze und Schrägbilddarstellungen anwenden können.
Worum es geht:
Die Schüler/innen sollen lernen, saubere Konstruktionen durchzuführen. Die Konstruktionen sollen in
der Regel die Größe eines DinA4 Blattes haben. Man arbeitet besser mit unlinierten Papier.
Hierdurch werden die Schüler gezwungen genau zu arbeiten, Winkel zu messen und Parallelen zu
erzeugen.
Die meisten Voralgen kann man als Folie mit dem OHP vorgeben oder als Vorlage für eine
Tischgruppe. Der Kopieraufwand bleibt so im Rahmen.
Die Fähigkeit dies auf dem Papier durchzuführen ist die Voraussetzung dafür, so etwas auch mit
dem Programm DynaGeo durchzuführen. Der Einsatz bietet sich hier an. Die Arbeitsaufträge sind
mit den statischen identisch.
Für das Thema „Prisma“ bietet Mathelive in den Lehrermaterialien ein Stationen-Lernen an. Dies
kann sinnvoll genutzt werden. Als ersten Schritt sollte man aber aus einem Netz ein Prisma bauen.
Dies Netz kann von Schülern selbst angefertigt werden. Es eignet sich gut ein Dreiecksprisma mit
einem gleichseitigen Dreieck als Grundfläche.
Die von den Schülern erstellten Produkte ergeben die Bewertung für diese Unterrichtssituation. Das
Thema „Unmögliche Figuren“ kann erst am Schluss realisiert werden. Wer keine
Schrägbilddarstellung anfertigen kann, kann auch keine unmögliche Figur zeichnen.
Wer mehr machen möchte, kann dies gerne tun. Als Erweiterungen bieten sich an die
●
isometrische Darstellung
●
die drei Tafel Projektion und die
●
zwei-Fluchtpunkt-Perspektive
Für alle Themen habe ich noch Materialien.
Diesen Tempel habe ich in
Paestum aufgenommen. Es ist
eine Zwei-FluchtpunktPerspektive.
Folie
Regeln für die Schrägbild-Perspektive:
●
●
●
cm
3,5cm
3cm
11
Die vorderen Flächen werden maßstabgetreu dargestellt.
Alle schräg nach hinten verlaufenden Linien werden um die
Hälfte verkürzt.
Die schräg nach hinten verlaufenden Linien bilden einen
45° Winkel mit der Horizontalen.
Für die Bemaßung werden die Maße des Originals
verwendet.
6,5cm
3cm
10
2,5cm
6,5cm
2cm
4cm
4,5cm
cm
8c
m
●
Arbeitsblatt
22
cm
Folie
1,5cm
2cm
2cm
1,5cm
10,5cm
3cm
2,5cm
4,5cm
6cm
1cm
1,5cm
2,5cm
15
Arbeitsauftrag:
●
Konstruiere das rechts
abgebildete Werkstück
(Maßstab 1:1) in der
Schrägbildperspektive.
●
Konstruiere ein zweites
Werkstück, das das untere zu
einem Quader ergänzt. Die
Gesamthöhe des Quaders
beträgt 8,5 cm. Die Maße des
oberen Werkstücks werden
berechnet.
3cm
cm
6cm
1cm
3cm
2cm
1cm
2cm
1,5cm
5,5cm
2,5cm
Folie
10,5cm
Arbeitsblatt
Arbeitsauftrag:
Zeichne ein Werkstück, das das abgebildete zu einem Quader ergänzt. Die beiden Werkstücke können
nur seitlich ineinander geschoben werden.
Arbeitsauftrag:
Zeichne das Schrägbild eines Würfels mit der Kantenlänge von 15 cm.
Konstruiere mithilfe der Seitendiagonalen die Mittelpunkte der Seitenflächen. Die
Seitendiagonalen werden wieder gelöscht.
Verbinde diese Punkte zu einem Oktaeder. Benutze hierfür eine andere Farbe.
Folie
Arbeitsblatt
Fluchtpunktperspektive:
●
Alle Vorderflächen werden maßstäblich konstruiert.
●
Alle nach hinten verlaufenden Linien verlaufen in Richtung des Fluchtpunktes. Sie sind
also nicht parallel.
●
Der Fluchtpunkt kann an einer beliebigen Stelle sitzen.
Arbeitsauftrag:
Überprüfe, ob die nach hinten verlaufenden Linien alle in Richtung auf den Fluchtpunkt
verlaufen.
Konstruiere eine Kiste, die in der Mitte des Raumes steht.
Konstruiere auf einem quer liegenden DinA4 Blatt die Ansicht eines Zimmers in der Fluchtpunkt
Perspektive.
C
D
Fluchtpunkt F
A
B
Arbeitsblatt