Seiten und Winkel am Dreieck

3
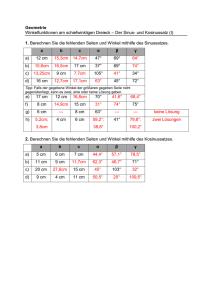
Seiten und Winkel am Dreieck
Gegeben sind eine Seite und die beiden anliegenden Winkel (wsw).
Beispiel:
Beschriftung eines Dreiecks
c = 6cm ,
α = 80° ,
β = 30°
g1
g2
Seite a liegt gegenüber des
Eckpunktes A , etc.
Konstruktionsbericht :
C
Beschriftung der Eckpunkte,
Seiten und Winkel erfolgt im
Gegenuhrzeigersinn!
α
β
A
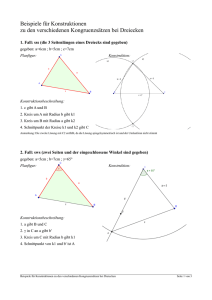
Dreieckskonstruktionen aus Seiten und Winkeln
4
Dreiecke lassen sich eindeutig konstruieren, wenn einer der vier folgenden Fälle gegeben ist:
1
a = 5cm ,
b = 4cm ,
Beispiel:
c = 5cm ,
b = 6cm ,
k2
C
a
b
c = AB
2.
k1 (B, a) ∩ k2 (A, b) = { C }
B
Gegeben sind zwei Seiten und der eingeschlossene Winkel (sws).
Beispiel:
c = 6cm ,
b = 5cm ,
α = 70°
g
C
Konstruktionsbericht :
k
b
α
A
k
b
c
A
2
Konstruktionsbericht :
1.
c
B
1.
c = AB
2.
< α in A an c → g
3.
k (A, b) ∩ g = { C }
< α in A an c → g1
3.
< β in B an c → g2
4.
g1 ∩ g2 = { C }
β = 50°
Konstruktionsbericht :
C
k1
2.
Gegeben sind zwei Seiten und der Winkel, der der grösseren Seite gegenüber liegt (Ssw).
g
c = 7cm
c = AB
B
c
Gegeben sind alle drei Seiten (sss).
Beispiel:
1.
β
A
c
B
1.
c = AB
2.
< β in B an c → g
3.
k (A, b) ∩ g = { C }