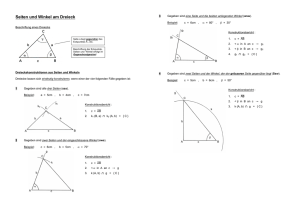
Geometrie Winkelfunktionen am schiefwinkligen Dreieck – Der
Werbung
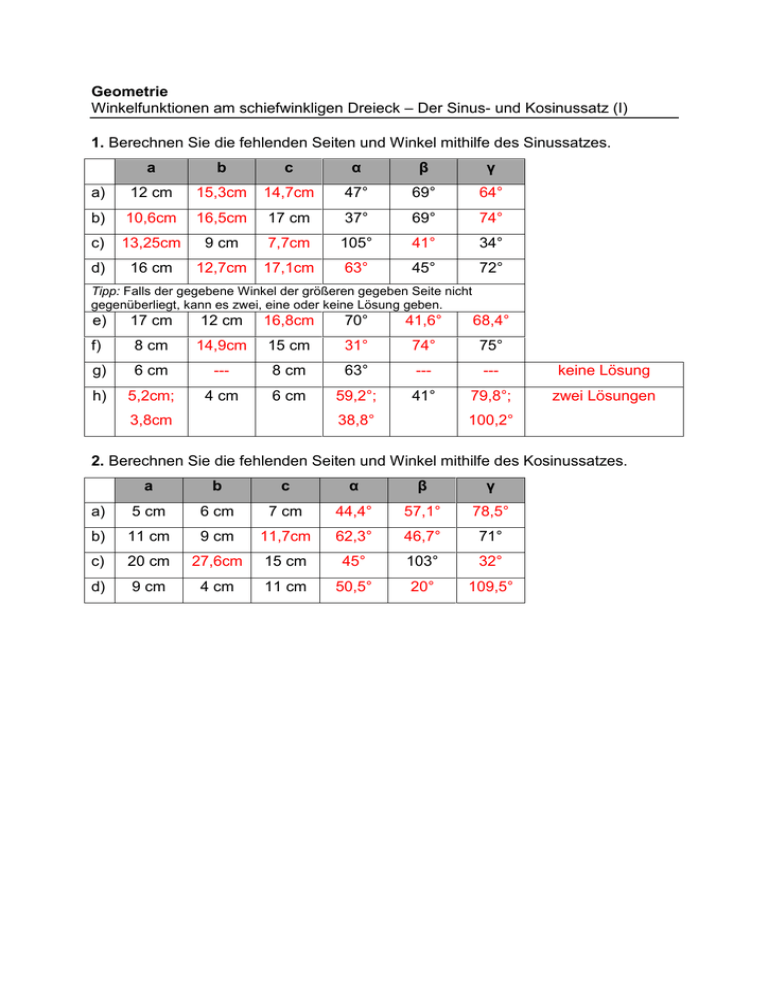
Geometrie Winkelfunktionen am schiefwinkligen Dreieck – Der Sinus- und Kosinussatz (I) 1. Berechnen Sie die fehlenden Seiten und Winkel mithilfe des Sinussatzes. a b c α β γ a) 12 cm 15,3cm 14,7cm 47° 69° 64° b) 10,6cm 16,5cm 17 cm 37° 69° 74° c) 13,25cm 9 cm 7,7cm 105° 41° 34° d) 16 cm 12,7cm 17,1cm 63° 45° 72° Tipp: Falls der gegebene Winkel der größeren gegeben Seite nicht gegenüberliegt, kann es zwei, eine oder keine Lösung geben. e) 17 cm 12 cm 16,8cm 70° 41,6° 68,4° f) 8 cm 14,9cm 15 cm 31° 74° 75° g) 6 cm --- 8 cm 63° --- --- keine Lösung h) 5,2cm; 4 cm 6 cm 59,2°; 41° 79,8°; zwei Lösungen 3,8cm 38,8° 100,2° 2. Berechnen Sie die fehlenden Seiten und Winkel mithilfe des Kosinussatzes. a b c α β γ a) 5 cm 6 cm 7 cm 44,4° 57,1° 78,5° b) 11 cm 9 cm 11,7cm 62,3° 46,7° 71° c) 20 cm 27,6cm 15 cm 45° 103° 32° d) 9 cm 4 cm 11 cm 50,5° 20° 109,5°