Word Pro - Klassenarbeit - Trigonometrie 2010 L - minus-p

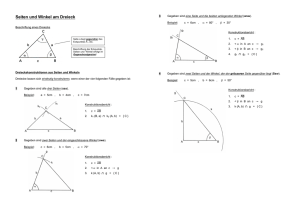
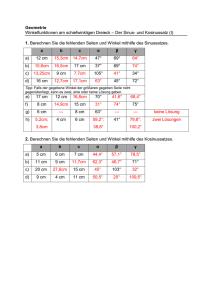
Name des Schülers: ______________________
Sportgymnasium Klasse 9/2
Lösungen: 3. Klassenarbeit - rechtwinklige Dreiecke
1. Zeichnen Sie jeweils ein Dreieck, für das die Gleichung gültig ist und
bezeichnen Sie die entsprechenden Seiten und Winkel.
(a ) a 2 + a 2 = b 2
(b ) sin ✍ = ac
(c ) tan ✒ = ef
(d ) h 2 = x $ y
f
c
b
α
x
ε
a
e
a
h
y
a
4P
2. Gegeben sind folgende Größen eines rechtwinkligen Dreiecks ABC:
a = 4, 5 cm ; ✎ = 35 o und ✏ = 90 o .
a) Begründen Sie, warum das Dreieck eindeutig definiert ist. (1P)
Es sind eine Seite und zwei anliegende Winkel gegeben.
Nach dem Kongruenzsatz (wsw) ist das Dreieck eindeutig definiert.
b) Berechnen Sie die fehlenden Seiten und Winkel des Dreiecks. (5P)
c2 = a2 + b2
✍ = 90 o − ✎
tan ✎ = b
a
c = a2 + b2
✍ = 90 o − 35 o
b = a $ tan ✎
✍ = 55 o
b = 4, 5cm $ tan 35 o
2
2
c = (4, 5cm ) + (3, 15cm )
b l 3, 15cm
c l 5, 5cm
6P
3. Gegeben ist ein Quader mit den Kantenlängen a = 10 cm, b = 7 cm, c = 6 cm.
a) Berechnen Sie die Länge der längsten Flächendiagonale. (2P)
f 21 = a 2 + b 2
2
2
f 1 = a 2 + b 2 = (10cm ) + (7cm )
f 1 l 12, 2cm
b) Berechnen Sie die Länge der Raumdiagonale des Quaders. (2P)
k2 = a2 + b2 + c2
2
2
2
k = a 2 + b 2 + c 2 = (10cm ) + (7cm ) + (6cm )
k l 13, 6cm
b) Berechnen Sie den Winkel, den die längste Flächendiagonale und die
Raumdiagonale einschließen. (2P)
tan ✬ = c = 6cm
sin ✬ = c = 6cm
f 1 12, 2cm
k 13, 6cm
✬ = arctan
✬ l 26, 2 o
6
12, 2
oder
✬ = arcsin
6
13, 6
✬ l 26, 2 o
6P
4. Eine 33 m hohe gerade Pyramide besitzt eine quadratische Grundfläche mit
den Maßen 51 m x 51 m.
a) Berechnen Sie die Größe der Winkel, die die Seitenflächen gegenüber der
Grundfläche besitzen. (2P)
tan ✒ = ha = 33m
25, 5m
2
✒ = arctan
33m
25, 5m
✒ l 52, 3 o
b) Berechnen Sie die Länge der Seitenkanten. (2P)
2
h 2a = a
2
ha =
a
2
+ h2
2
2
2
+ h 2 = (25, 5m ) + (33m )
h a l 41, 7m
2
s2 = a
2
s=
a
2
+ h 2a
2
2
2
+ h 2a = (25, 5m ) + (41, 7m )
s l 48, 9m
c) Berechnen Sie den Oberflächeninhalt der Pyramide. (2P)
a $ ha
Ao = a2 + 4 $
= a 2 + 2ah a
2
2
A o = (51m ) + 2 $ 51m $ 41, 7m
A o l 6854, 4m
6P
5. Ein gleichseitiges Dreieck hat einen Umfang von 21 cm.
a
h
a
2
a) Berechnen Sie die Höhe des Dreiecks. (2P)
u = a + a + a = 3a
a = 21cm + 3
a = 7cm
a2 = h2 + a
2
2
h = a2 − a
2
h l 6, 06cm
2
2
2
= (7cm ) − (3, 5cm )
b) Berechnen Sie den Flächeninhalt des Dreiecks. (2P)
A= a$h
2
7cm $ 6, 06cm
A=
2
A l 21, 21cm 2
4P
6. Ein 41 m hoher Turm steht 93 m von einem Fluss entfernt. Von der Turmspitze
aus erscheint die Flussbreite unter dem Winkel ✍ = 5, 2 o .
Berechnen Sie die Breite des Flusses. (2P)
tan ✎ = e = 93m
h 41m
✎ l 66, 2 o
tan(✎ + ✍ ) = e + b
h
e + b = tan(✎ + ✍ ) $ h
e + b = tan(71, 4 o ) $ 41m
e + b l 121, 8m
b = 121, 8m − 93m
b l 28, 8m
Der Fluss ist etwa 29 m breit.
2P