Unterrichtsentwurf

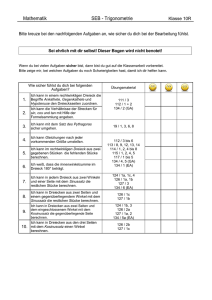
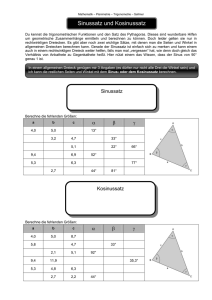
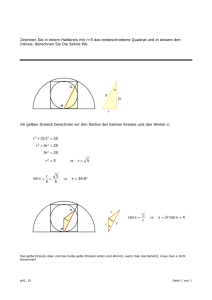
Klasse 10 Mathematik
Musterlösung S. 195, S. 197
Kra, 8. Juni 2004
S. 195
25 b: Die Höhe h lässt sich links und rechts anzeichnen (im Bild ist sie nur links). Es entstehen dann rechtwinklige
Dreiecke mit den Winkel 180° -  (linkes Dreieck) und  (rechtes Dreieck).
Mit Hilfe von sin = G/H lassen sich jetzt die beiden schwarzen Linien ausrechnen.
Dann mit cos-Satz ( -  liefert den Winkel), sollte Flussbreite entstehen: ca. 80 m
25 c: Mit dem Sinussatz lassen sich alle Seiten im auf dem Boden liegenden Dreieck ausrechnen. (Der fehlende
Winkel berechnet sich durch 180°-  - )
Dann kann man über eins der beiden Seitendreiecke (rechtwinklig!) die Höhe berechnen, indem man tan benutzt!
Wegen Rundungen kommen links und rechts verschiedene Werte so um 495 m raus!
S. 197
30: Über den Sinussatz lassen sich |AQ| (= 5,871 km) berechnen und |AP| (=3,069 km) berechnen.
Dann 1 - 2 und Kosinussatz und schon hat man |PQ| = 4,311 km.
Man kann natürlich auch über BP und BQ rechnen!