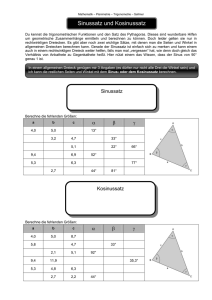
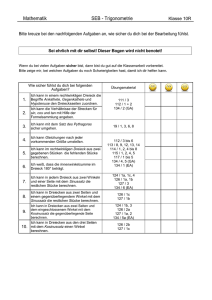
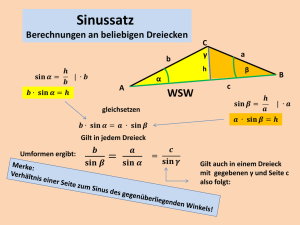
a b c sin sin sin = = α β γ a² b² + c² - 2bc cos b² a² + c²

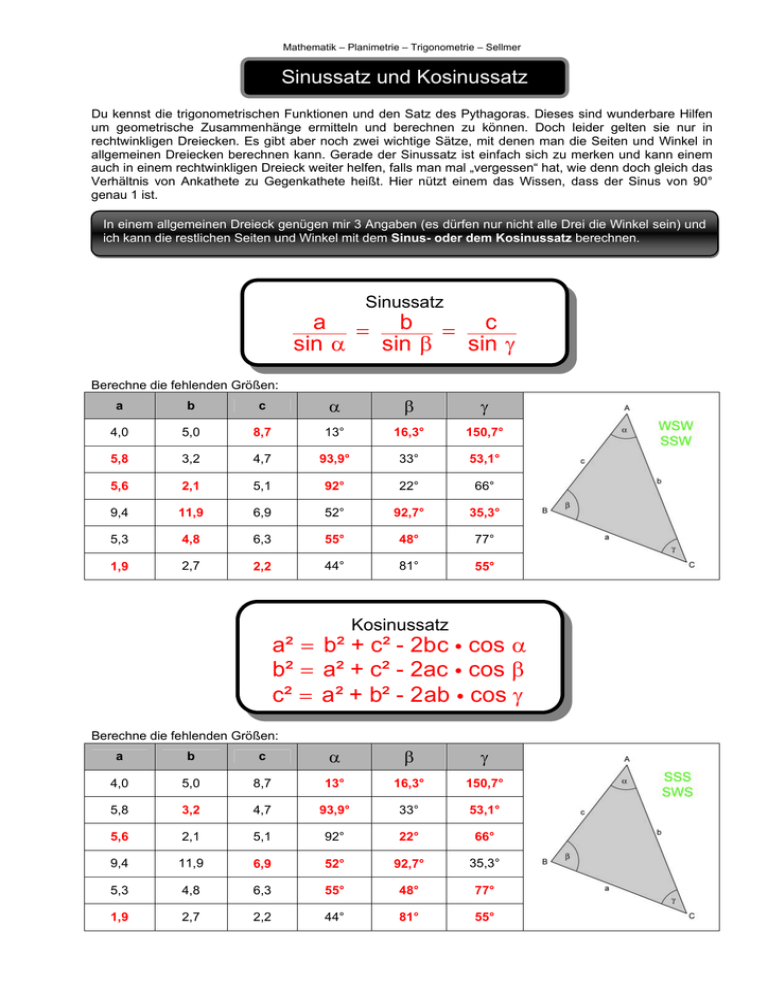
Mathematik – Planimetrie – Trigonometrie – Sellmer
Sinussatz und Kosinussatz
Du kennst die trigonometrischen Funktionen und den Satz des Pythagoras. Dieses sind wunderbare Hilfen
um geometrische Zusammenhänge ermitteln und berechnen zu können. Doch leider gelten sie nur in
rechtwinkligen Dreiecken. Es gibt aber noch zwei wichtige Sätze, mit denen man die Seiten und Winkel in
allgemeinen Dreiecken berechnen kann. Gerade der Sinussatz ist einfach sich zu merken und kann einem
auch in einem rechtwinkligen Dreieck weiter helfen, falls man mal „vergessen“ hat, wie denn doch gleich das
Verhältnis von Ankathete zu Gegenkathete heißt. Hier nützt einem das Wissen, dass der Sinus von 90°
genau 1 ist.
In einem allgemeinen Dreieck genügen mir 3 Angaben (es dürfen nur nicht alle Drei die Winkel sein) und
ich kann die restlichen Seiten und Winkel mit dem Sinus- oder dem Kosinussatz berechnen.
Sinussatz
a  b  c
sin 
sin 
sin 
Berechne die fehlenden Größen:
a
b
c



4,0
5,0
8,7
13°
16,3°
150,7°
5,8
3,2
4,7
93,9°
33°
53,1°
5,6
2,1
5,1
92°
22°
66°
9,4
11,9
6,9
52°
92,7°
35,3°
5,3
4,8
6,3
55°
48°
77°
1,9
2,7
2,2
44°
81°
55°
Kosinussatz
a²  b² + c² - 2bc  cos 
b²  a² + c² - 2ac  cos 
c²  a² + b² - 2ab  cos 
Berechne die fehlenden Größen:
a
b
c



4,0
5,0
8,7
13°
16,3°
150,7°
5,8
3,2
4,7
93,9°
33°
53,1°
5,6
2,1
5,1
92°
22°
66°
9,4
11,9
6,9
52°
92,7°
35,3°
5,3
4,8
6,3
55°
48°
77°
1,9
2,7
2,2
44°
81°
55°