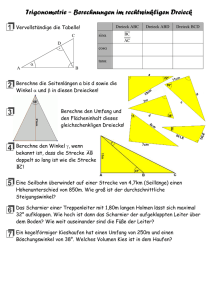
4. Aufgaben zum schiefwinkeligen Dreieck: In der folgenden Tabelle

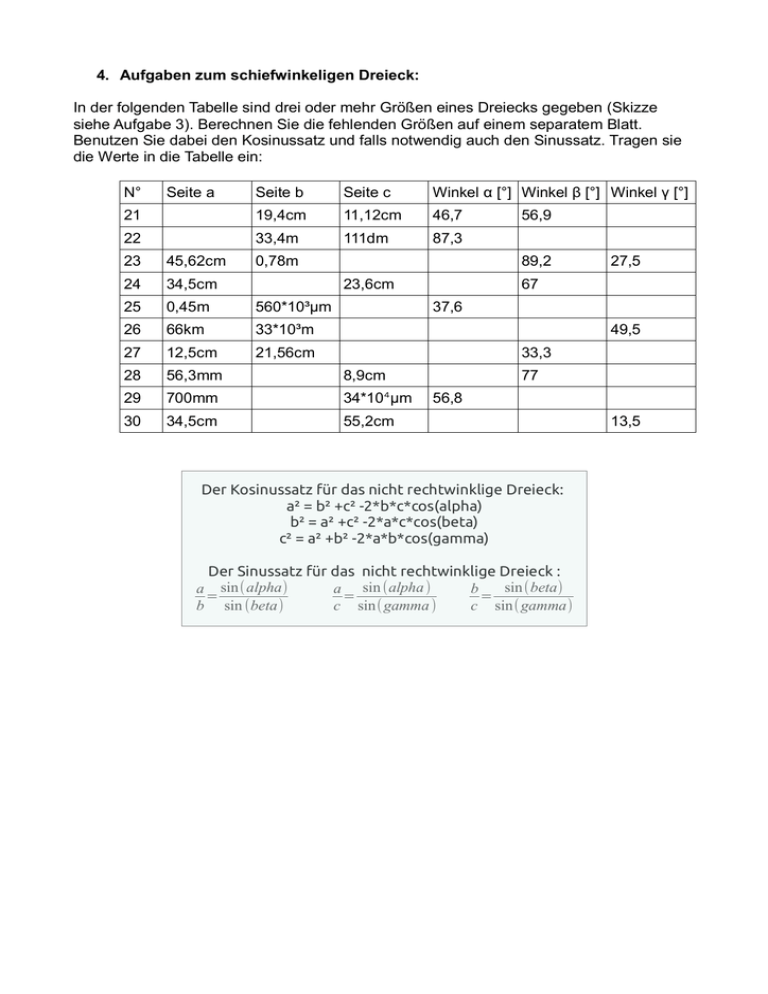
4. Aufgaben zum schiefwinkeligen Dreieck:
In der folgenden Tabelle sind drei oder mehr Größen eines Dreiecks gegeben (Skizze
siehe Aufgabe 3). Berechnen Sie die fehlenden Größen auf einem separatem Blatt.
Benutzen Sie dabei den Kosinussatz und falls notwendig auch den Sinussatz. Tragen sie
die Werte in die Tabelle ein:
N°
Seite a
Seite b
Seite c
Winkel α [°] Winkel β [°] Winkel γ [°]
21
19,4cm
11,12cm
46,7
22
33,4m
111dm
87,3
23
45,62cm
0,78m
24
34,5cm
25
0,45m
560*10³μm
26
66km
33*10³m
27
12,5cm
21,56cm
28
56,3mm
8,9cm
29
700mm
34*10⁴μm
30
34,5cm
55,2cm
56,9
89,2
23,6cm
27,5
67
37,6
49,5
33,3
77
56,8
Der Kosinussatz für das nicht rechtwinklige Dreieck:
a² = b² +c² -2*b*c*cos(alpha)
b² = a² +c² -2*a*c*cos(beta)
c² = a² +b² -2*a*b*cos(gamma)
Der Sinussatz für das nicht rechtwinklige Dreieck :
sin(beta)
a sin(alpha)
a sin (alpha )
b
=
=
=
b sin (beta)
c sin(gamma )
c sin(gamma)
13,5