Übungsblatt 1
Werbung

Institut für Algebra and Geometrie
Prof. Dr. Enrico Leuzinger
M. Sc. Moritz Gruber
Hyperbolische Geometrie
Sommer-Semester 2016
Übungsblatt 1
Aufgabe 1
19.04.2016
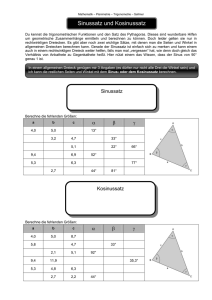
(Sinussatz und Kosinussatz)
Für zwei Strahlen g(t) := tv + w und h(s) := su + w mit u, v, w ∈ R2 , s, t ∈ R≥0 ist
der Winkel im Schnittpunkt w definiert als die eindeutig bestimmte Zahl η ∈ [0, π ]
mit
< v, u >
cos(η ) =
kvkkuk
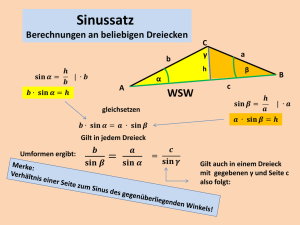
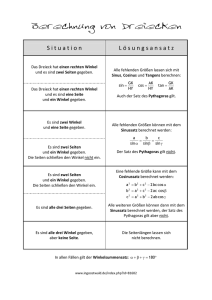
Es sei nun ∆ABC ein Dreieck in der euklidischen Ebene E2 mit Kanten der Länge
a, b und c (jeweils gegenüber von A, B bzw. C) und sei α = ]CAB der Winkel bei A,
sowie β und γ die Winkel bei B bzw. C.
Zeigen Sie, dass dann gilt:
1)
a
sin α
2)
c2 = a2 + b2 − 2ab cos(γ)
=
Aufgabe 2
b
sin β
=
c
sin γ
(Sinussatz)
(Kosinussatz)
(Involution)
Es sei I : C −→ C definiert durch
1
z
I( z ) : = ∞
0
für z ∈ C \ {0}
für z = 0
für z = ∞
Zeigen Sie, dass I stetig ist.
Aufgabe 3
(Stereographische Projektion)
Zeigen Sie, dass die erweiterte stereographische Projektion
σ : S2 −→ C
ein Homöomorphismus ist.
Das heißt, σ ist bijektiv und σ und σ−1 sind stetig.