Herleitung Sinussatz und Kosinussatz

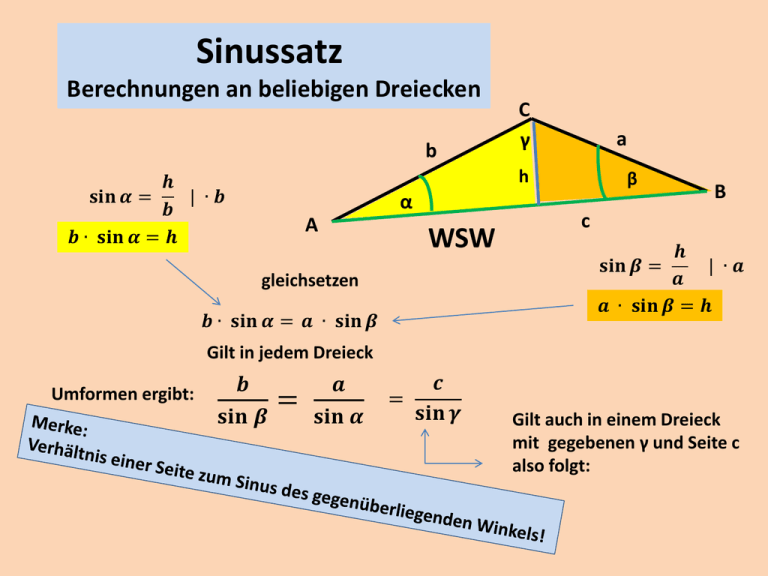
Sinussatz
Berechnungen an beliebigen Dreiecken
b
C
γ
a
h
𝒉
𝐬𝐢𝐧 𝜶 =
| ∙𝒃
𝒃
𝒃 ∙ 𝐬𝐢𝐧 𝜶 = 𝒉
α
A
WSW
gleichsetzen
𝒃 ∙ 𝐬𝐢𝐧 𝜶 = 𝒂 ∙ 𝐬𝐢𝐧 𝜷
β
B
c
𝒉
| ∙𝒂
𝒂
𝒂 ∙ 𝐬𝐢𝐧 𝜷 = 𝒉
𝐬𝐢𝐧 𝜷 =
Gilt in jedem Dreieck
Umformen ergibt:
𝒃
𝐬𝐢𝐧 𝜷
=
𝒂
𝐬𝐢𝐧 𝜶
𝒄
=
𝐬𝐢𝐧 𝜸
Gilt auch in einem Dreieck
mit gegebenen γ und Seite c
also folgt:
Sinussatz
Berechnungen an beliebigen Dreiecken
geg.: b= 6 cm
α = 35°
γ = 122°
C
γ
b
a
h
β
α
A
ges.: β; a; c
WSW
B
c
1. Berechne den dritten Winkel.
β = 180° - (α + γ ) = 180° - 157°= 23°
2. Wähle die passende Verhältnisgleichung
nach Sinussatz um a zu berechnen:
𝒃
𝒂
=
| ∙ sin 𝜶
𝐬𝐢𝐧 𝜷
𝐬𝐢𝐧 𝜶
𝟔 𝐜𝐦 ∙ 𝐬𝐢𝐧 𝟑𝟓°
= 8,81 cm
𝒂=
𝐬𝐢𝐧 𝟐𝟑°
3. Berechne c mit passender …. :
𝒃
𝐬𝐢𝐧 𝜷
=
𝒄
𝐬𝐢𝐧 𝜸
𝒄=
𝟔 𝐜𝐦 ∙ 𝐬𝐢𝐧 𝟏𝟐𝟐°
= 13,02 cm
𝐬𝐢𝐧 𝟐𝟑°
| ∙ sin 𝜸
Kosinussatz bei SWS und SSS
C
γ
b² = x² + h²
b
𝒙
𝒃
𝐜𝐨𝐬 𝜶 =
x = b ∙ 𝐜𝐨𝐬 𝜶
h
α
A
a² = h² + y²
a² = h² + ( c – x )²
x
a
y
c
SWS
β
c=x+y
y=c-x
einsetzen
Bin. Formel
a² = h² + c² - 2cx + x² | sortieren
einsetzen
a² = c² - 2cx + x²+ h²
a² = c² - 2cx + b² | sortieren
muss nur noch das x
a² = b² + c² - 2 c x Nun
ersetzt werden!
a² = b² + c² - 2 c b cos α fertig ist der……
B
Kosinussatz bei SWS
Du willst die 3. Seite berechnen.
cos des eingeschlossenen Winkels
Nimm die Summe der
Quadrate der beiden anliegenden Seiten
b
C
γ
h
α
A
Nun denke an die 2. Bin.Formel……
a
β
c
- minus dem doppelten Produkt
der gegebenen Seiten
mal cos des eingeschlossenen Winkels
a² = b² + c² - 2 b c · cos α
B
Kosinussatz bei SSS
b
C
γ
h
a
β
α
Die Winkel sind
c
A
gesucht:
1. Winkel mit Kosinussatz berechnen!
Gleichung umformen nach cos α
B
a² = b² + c² - 2 c b cos α | + 2bc·cosα
2bc ∙cosα +a² = b² + c² | - a²
2 bc cos α = b² + c² - a² |: 2bc
b² + c²- a²
Vorsicht bei der Eingabe im TR!!
= cos α
2 bc
2. Winkel mit Sinussatz berechnen.
3. Winkel über Winkelsumme