Kosinussatz

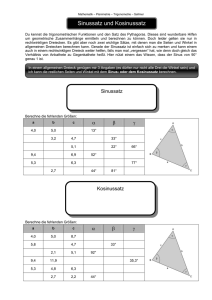
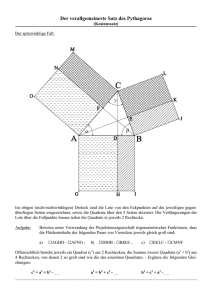
Kosinussatz
In einem Dreieck gilt für den der Seite AB gegenüberliegenden Winkel γ
c 2 = a2 + b 2 − 2ab cos γ .
B
c
a
γ
A
b
Kosinussatz
1-1
Kosinussatz
In einem Dreieck gilt für den der Seite AB gegenüberliegenden Winkel γ
c 2 = a2 + b 2 − 2ab cos γ .
B
c
a
γ
A
b
Als Spezialfall erhält man für γ = π/2 den Satz des Pythagoras:
c 2 = a2 + b 2 .
Kosinussatz
1-2
Beweis:
a
γ
c
h
q
p
b
Kosinussatz
2-1
Beweis:
a
γ
c
h
q
p
b
Satz des Pythagoras
=⇒
c 2 = h2 + q 2 ,
h 2 = a2 − p 2
mit q = b − p, p = a cos γ
Kosinussatz
2-2
Beweis:
a
γ
c
h
q
p
b
Satz des Pythagoras
=⇒
c 2 = h2 + q 2 ,
h 2 = a2 − p 2
mit q = b − p, p = a cos γ
Einsetzen
c 2 = (a2 − p 2 ) + (b − p)2
= a2 − p 2 + b 2 − 2b(a cos γ) + p 2
= a2 + b 2 − 2ab cos γ
Kosinussatz
2-3