Lösung als Word-Dokument (*)

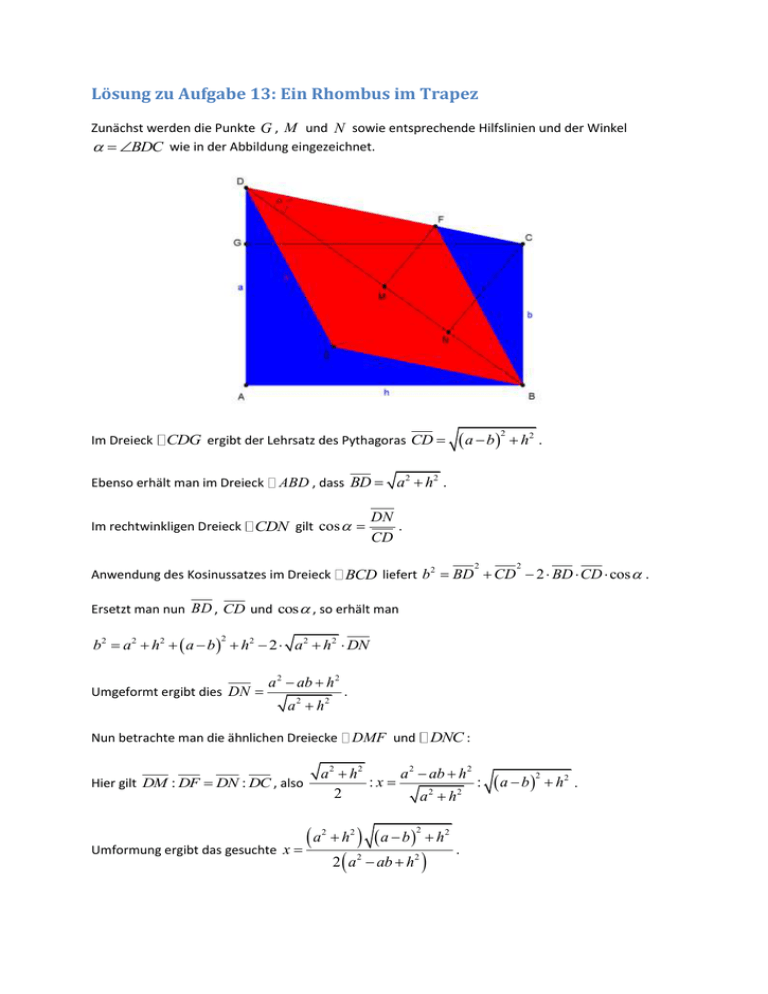
Lösung zu Aufgabe 13: Ein Rhombus im Trapez
Zunächst werden die Punkte G , M und N sowie entsprechende Hilfslinien und der Winkel
  BDC wie in der Abbildung eingezeichnet.
Im Dreieck CDG ergibt der Lehrsatz des Pythagoras CD 
Ebenso erhält man im Dreieck
 a  b
2
 h2 .
ABD , dass BD  a 2  h2 .
Im rechtwinkligen Dreieck CDN gilt cos  
DN
.
CD
2
2
BCD liefert b 2  BD  CD  2  BD  CD  cos  .
Anwendung des Kosinussatzes im Dreieck
Ersetzt man nun BD , CD und cos  , so erhält man
b2  a2  h2   a  b   h2  2  a 2  h2  DN
2
Umgeformt ergibt dies DN 
a 2  ab  h 2
a 2  h2
Nun betrachte man die ähnlichen Dreiecke
Hier gilt DM : DF  DN : DC , also
.
DMF und DNC :
a 2  h2
a 2  ab  h 2
:x
:
2
a 2  h2
a
Umformung ergibt das gesuchte x 
2
 h2 
a  b
2
 h2
2  a 2  ab  h2 
.
a  b
2
 h2 .