Übungen zu Frage 197 - Mathematik

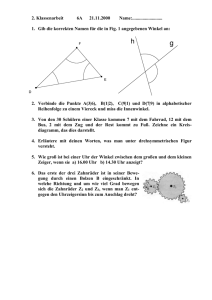
Übungen
Analytische Geometrie – Winkelberechnungen
Übungen zu Frage 197:
Gegeben ist die Raute ABCD mit A(0|4|0), B(0|0|2) und C(4|0|0) und D(4|4|−2).
Berechnen Sie die Innenwinkel der Raute.
(Die Lösung finden Sie auf Seite 2.)
© Mathematik-Verlag, www.matheverlag.com
-1-
Lösung:
In einer Raute sind die gegenüberliegenden Innenwinkel gleich groß.
B
Es gilt also: α = γ und β = δ
β
Der Winkel α ist der Winkel zwischen den Vektoren
 0 
 4 
 
 
AB =  − 4  und AD =  0  .
 2 
− 2
 
 
C γ
δ
(Hinweis: Man beachte die Pfeilrichtungen ! Um einen Innenwinkel zu berechnen,
müssen die Pfeile vom entsprechenden Eckpunkt wegzeigen.)
Einsetzen von | AB | =
Formel cos α =
cos α =
−4
20
20 , | AD | =
AB ⋅ AD
| AB | ⋅ | AD |
α A
D
20 und AB · AD = − 4 in die
ergibt:
⇒ α = 101,5° und γ = 101,5°
 4 
 0 
 
 
Der Winkel β ist der Winkel zwischen den Vektoren BC =  0  und BA =  4  .
− 2
− 2
 
 
Einsetzen von | BA | =
ergibt: cos β =
4
20
20 , | BC | =
20 und BA · BC = 4 in die Formel cos β =
⇒ β = 78,5° und δ = 78,5°
© Mathematik-Verlag, www.matheverlag.com
-2-
BA ⋅ BC
| BA | ⋅ | BC |