doc - Digitale Schule Bayern

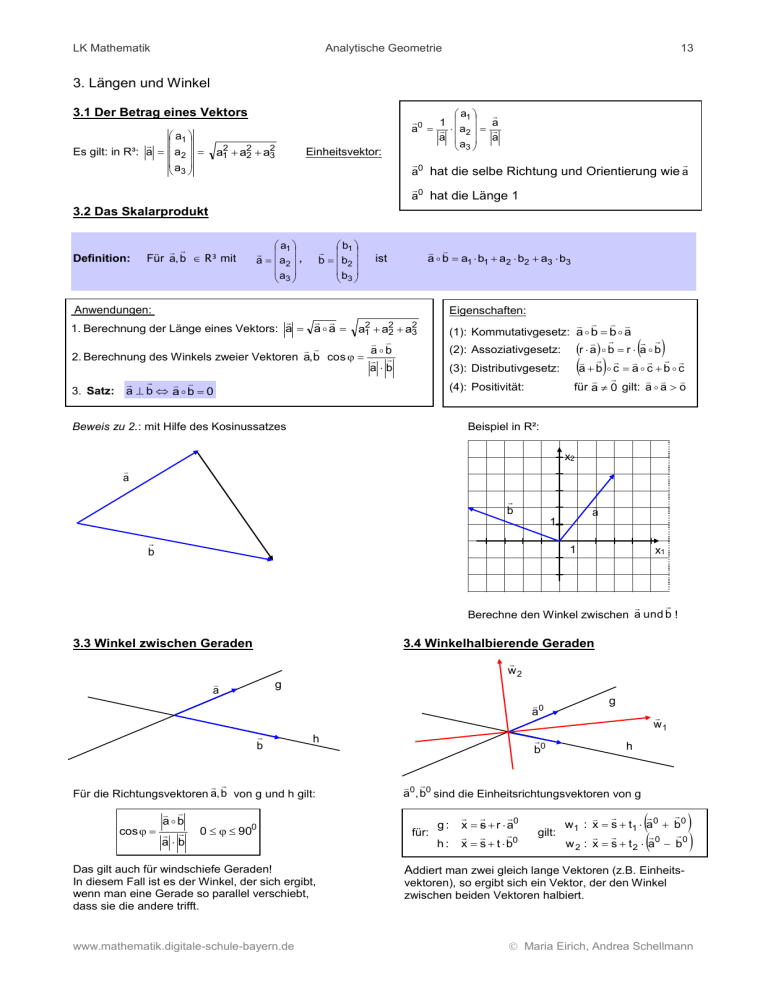
LK Mathematik
Analytische Geometrie
13
3. Längen und Winkel
3.1 Der Betrag eines Vektors
a 
  1
Es gilt: in R³: a   a2  
a 
 3
a12  a22  a32
Einheitsvektor:
 a1 
0
1  
a     a2  
a  
 a3 

a

a


a0 hat die selbe Richtung und Orientierung wie a

a0 hat die Länge 1
3.2 Das Skalarprodukt
Definition:
 
Für a, b  R³ mit
a 
  1
a   a2  ,
a 
 3
b 
  1
b   b2 
b 
 3
 
a  b  a1  b1  a2  b2  a3  b3
ist
Anwendungen:

 
1. Berechnung der Länge eines Vektors: a  a  a 
Eigenschaften:
a12
 a22
 
 
ab
2. Berechnung des Winkels zweier Vektoren a, b cos    
ab
 
 
3. Satz: a  b  a  b  0
   
(1): Kommutativgesetz: a  b  b  a
 
 
(2): Assoziativgesetz: r  a   b  r  a  b
      
ab c  ac bc
(3): Distributivgesetz:
  
 
(4): Positivität:
für a  0 gilt: a  a  o
 a32

Beweis zu 2.: mit Hilfe des Kosinussatzes
 

Beispiel in R²:
x2

a

b

a
1

b
1
x1


Berechne den Winkel zwischen a und b !
A(2/1)
3.3 Winkel zwischen Geraden
3.4 Winkelhalbierende Geraden

w2

a
g

a0

b
h
 
Für die Richtungsvektoren a, b von g und h gilt:
 
ab
cos    
ab
0    900
Das gilt auch für windschiefe Geraden!
In diesem Fall ist es der Winkel, der sich ergibt,
wenn man eine Gerade so parallel verschiebt,
dass sie die andere trifft.
www.mathematik.digitale-schule-bayern.de

b0
g

w1
h
 
a0 , b0 sind die Einheitsrichtungsvektoren von g
für:
g:
h:

 
x  s  r  a0

 
x  s  t  b0



 
w 1 : x  s  t1  a 0 
gilt:

 
w 2 : x  s  t 2  a0 

b0

b0


Addiert man zwei gleich lange Vektoren (z.B. Einheitsvektoren), so ergibt sich ein Vektor, der den Winkel
zwischen beiden Vektoren halbiert.
 Maria Eirich, Andrea Schellmann