Mathematik

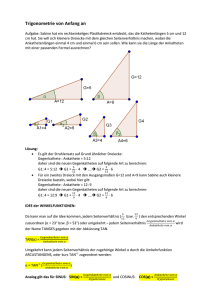
Mathematik
Lektion 6
Winkelfunktionen
1
Mathematische Hintergründe
r=1
Die Wichtigen Formeln in unserem rechtwinkligen Dreieck sind:
b
α
c
a
·
Länge der Gegenkathete
a
=
Länge der Hypothenuse
c
Länge der Ankathete
a
Kosinus: cos(α) =
=
Länge der Hypothenuse
c
Länge der Gegenkathete
a
Tangens: tan(α) =
=
Länge der Ankathete
b
Länge der Ankathete
b
(Kotangens: cot(α) =
= )
Länge der Gegenkathete
a
Sinus: sin(α) =
Mithilfe der Winkelfunktionen kann man also stets alle Winkel berechnen. Man
benötigt nur die Längen der zugehörigen Seiten. Umgekehrt kann man aber auch
die Seiten berechnen, wenn man die Winkel gegeben hat.
Ich beschränke mich hier auf die Betrachtung des Winkels Alpha (α). Der Gegebüberliegende Winkel Beta (β) kann in gleicher Weise berechnet werden. Hierzu
dreht man quasi das Dreieck um und Ankathete und gegenkathete tauschen in
den Formeln den Platz.
ACHTUNG: Vergesst nicht dass es auch noch den Satz des Pythagoras gibt,
also: a2 + b2 = c2 .
Wenn man also zwei Seitenlängen gegeben hat und die dritte Seite sucht kommt
man mit den Winkelfunktionen nicht (sehr schwierig) weiter!
1
2
Berechnung
Ist ein Winkel und eine Seite gegeben, so kann man damit jede beliebige Seite
berechnen. Hierzu sucht man sich die Formel rau§ in der die Gegebene und gesuchte Seite auftaucht und stellt diese nach der gesuchten Seite um.
Beispiel 1:
Gegeben: α = 53 c = 2
Gesucht: a
a
Lösung: Die Formel die uns weiter hilft ist hier: sin(α) =
c
Wir stellen sie nach dem gesuchten a um: a = sin(α) · c
und berechnen a: a = sin(53) · 2 ≈ 1, 6
Beispiel 2:
Gegeben: α = 47 a = 3
Gesucht: b
a
Lösung: Die Formel die uns weiter hilft ist hier: tan(α) =
b
a
Wir stellen sie nach dem gesuchten a um: b =
tan(α)
3
Und berechnen a: a =
≈ 2, 8
tan(47)
Wenn ich nun zwei Seiten gegeben habe und einen Winkel suche, so muss ich
wieder die Formel suchen, in der die zwei Seiten vorkommen. Dann berechnet
man den Bruch. Nun muss man allerdings die Umkehrfunktion zur jeweiligen
Winkelfunktion bilden, das heißt:
Winkelfunktion Umkehrfunktion
auf dem Taschenrechner
Sinus
Arkussinus
sin−1 oder asin oder arcsin
Kosinus
Arkuskosinus
cos−1 oder acos oder arccos
Tangens
Arkustangens
tan−1 oder atan oder arctan
Beispiel 3:
Gegeben: b = 2 a = 3
Gesucht: α
a
Lösung: Die Formel die uns weiter hilft ist hier: tan(α) =
b
3
Umstellen brauchen wir hier nicht. Berechnen des Bruches: = 1, 5
2
und nun den Arkustangens: tan−1 (1, 5) ≈ 56, 3
Besser ist es, wenn man in den Taschenrechner direkt den Bruch eintippt um
Rundungsfehler zu vermeiden, also hier: α = tan−1 (3/2) ≈ 56, 3
Beispiel 4:
Gegeben: c = 4, 73 a = 12, 8
Gesucht: α
a
Lösung: Die Formel die uns weiter hilft ist hier: sin(α) =
c
12, 8
Umstellen brauchen wir hier nicht. Berechnen des Bruches:
≈ 2, 72
4, 73
und nun den Arkussinus: sin−1 (2, 72) ≈ 69, 8
Direkt im Taschenrechner: α = sin−1 (12,8/4,73) ≈ 69, 7
2
Aufgabe 2.1 Berechnen Sie die fehlenden Seiten.
β
b
Wir betrachten stets das Dreieck:
129. α = 30◦
a=3
130. α = 46◦
b=3
131. β = 30
c=3
132. a = 3
◦
α
a
·
c
b=4
133. β = 22◦
b=3
134. β = 26, 81◦
135. α = 66, 6◦
a=3
c=3
Aufgabe 2.2 Berechnen Sie die fehlenden Winkel.
Geben Sie den Winkel wenn nötig in Grad/Minuten/Sekunden an.
β
b
Wir betrachten stets das Dreieck:
α
a
·
c
Hinweis: Die Winkelsumme im Dreieck beträgt stets 180◦
136. b = 7 a = 3
137. c = 7
a=3
138. b = 7 c = 3
139. b = 3a a = 1, 5
140. b = 2, 3x a = 1, 5x
141. b =
12
7
a=
17
15
Aufgabe 2.3 Ein Flugzeug besitzt einen idealen Anflugwinkel von 37◦ .
(d.h. optimaler Winkel zur Landung, vom Boden aus gemessen)
Der Pilot möchte die Landung bei 800 Höhenmetern beginnen.
Wieviele Meter vor der Landebahn muss er mit seiner Landung beginnen?
Machen Sie sich den Sachverhalt zuewrst anhand einer Skizze klar.
(Lös: 1386m)
Aufgabe 2.4 Betrachten Sie das unten angefügte Bild.
Ein, 1,7 Meter großer, Mann läuft in der Fußgängerzone 2m hinter einer Frau.
Die Frau hat einen Rock an und Zeigt 70cm Bein.
Welchen Sichtwinkel muss der Mann besitzen um die Beine der Frau zu betrachten, wenn er 2m hinter der Frau läuft?
3